目录
JS中的位运算
JS中的与运算
JS中的或运算
JS中的否(非)运算
计算机中负数的存储方式
JS中的异或运算
JS中位运算的应用场景
位的叠加(开关)
JS中的位移运算
左位移
右位移
全右位移
首先了解一下什么是位运算
位运算:从现代计算机中所有的数据二进制的形式存储在设备中。即 0、1 两种状态,计算机对二进制数据进行的运算(+、-、*、/)都是叫位运算,即将符号位共同参与运算的运算。
上面的话可以简化为:将一个整数的二进制格式进行运算
那么在JS中是如何进行位运算的呢?
JS中的位运算
在JS中,如果需要对一个数据,类似于加减乘除,它会首先将其转换为一个整数,并且按照32位的整数二进制排列
举个例子:小数2.3
2.3 -> 2 -> 0000 0000 0000 0000 0000 0010 //第一个0表示符号位,1为负数,0为正数首先把2.3四舍五入成一个整数2,然后将这个整数转换成32位二进制整数格式,所以对于JS中的位运算,需要全部转换成整数格式,在进行运算
那么对于一些特殊的数字,比如NaN、infinity、-infinity是怎么表示的呢
在JS中规定。对于特殊的以上数字,如果进行位运算,全部看作0
JS中的与运算
在js中位运算有多种,先介绍第一种与运算,符号为:&,写法为:表达式1 & 表达式2
那么与运算是怎么计算的呢?
与运算:参加运算的两个数据,按二进制位进行“与”运算
上面的话通俗来讲:两位同时为“1”,结果才为“1”,否则为0,就是将两个整数的每一个二进制位进行比较,如果都为1,结果才为1,其余情况全部为0;
举个例子 : 1 & 2
1 & 2
1 对应的二进制是--0000 0000 0000 0000 0000 0000 0000 0001
2 对应的二进制是--0000 0000 0000 0000 0000 0000 0000 0010
由于前28位都为0,结果与运算后肯定也全为0,这时就算后四位
- 0 0 0 1 -
- 0 0 1 0 -
-----------
- 0 0 0 0 - //结果为0000,转换为十进制为0,那么1 & 2的结果就为0JS中的或运算
在js中的第二种位运算是或运算,符号 | ,写法:表达式1 | 表达式2
那么或运算是如何计算的呢?
或运算:将比较的两个整数,先转换为32位二进制,然后每一位进行比较,全0才为0,其余情况全为1
举个例子 : 1 | 3
1 | 3
1 对应的二进制是--0000 0000 0000 0000 0000 0000 0000 0001
3 对应的二进制是--0000 0000 0000 0000 0000 0000 0000 0011
由于前30位全为0,与运算后也全为0,可以不计入计算
- 0 1 -
- 1 1 -
-------
- 1 1 - //二进制11,需要补齐32位才可以转换为十进制,那么1 | 3的结果就为3JS中的否(非)运算
在js中,还有一中运算,称为否或者非运算,符号为:~,写法:~表达式
否运算:将这个整数全部二进制位按位取反,0变成1,1变成0
在这里首先带大家了解一下知识
计算机中负数的存储方式
可能某些同学认识二进制会认为负数-1在计算机是这样存储的
-1
> 1000 0000 0000 0000 0000 0000 0000 0001 //符号位为-表示负数,最后一位为1,表示1感觉上-1好像是这样存储的,但其实计算机并不是这样存储的,这样的表示方法叫做真码,对于人来说,这样确实很任意让人阅读,对于为什么计算机会这样存储,这与计算机组成原理有关,计算机是不能做减法的,只能做加法的,这里并不多讲
那么计算机到底是如何存储负数的呢?
首先计算机拿出负数的真码,符号位不动,其余位全部取反,取反的叫反码,然后将反码加上1就可以得到负数的补码,在计算机中负数就是存储的补码
如果还不懂的话,请看我举个例子:如 -1
-1
拿出真码 --> 1000 0000 0000 0000 0000 0000 0000 0001 // 也叫原码
得到反码 --> 1111 1111 1111 1111 1111 1111 1111 1110 // 真码取反
得到补码 --> 1111 1111 1111 1111 1111 1111 1111 1111 // 反码加1由上述方法,那么-1在计算机存储的就是补码:1111 1111 1111 1111 1111 1111 1111 1111
注意:以上方法只针对负数存储,正数在计算机中,原反补码相同
通过上述问题你是否知道 ~1等于多少,如果还不懂,请听我慢慢讲
~1
1 对应的二进制是 --> 0000 0000 0000 0000 0000 0000 0000 0001
~1 对1的二进制序列进行取反 --> 1111 1111 1111 1111 1111 1111 1111 1110
这是得到的是存储在计算机中的补码,需要转换成真码,然后才能传换成十进制
> 取出补码 --> 1111 1111 1111 1111 1111 1111 1111 1110
> 得到反码 --> 1111 1111 1111 1111 1111 1111 1111 1101 //补码-1就得到反码
> 得到真码 --> 1000 0000 0000 0000 0000 0000 0000 0010 //符号位不变,其余全部取反,得到真码
> 转换成十进制 ----得到-2
--所以 ~1 的结果为 -2以上方法确实可以得出非运算结果,但看起来繁琐复杂,这里小编给大家介绍一个简单的使用方法,面试笔试,考试快速得出结果
~x:-x - 1 // 取反某个数字,先让这个数字变成负数,然后减去1,就得到非运算结果
举个例子 ~2和~-2
~2 = -2 - 1 = -3
~-2 = 2 - 1 = 1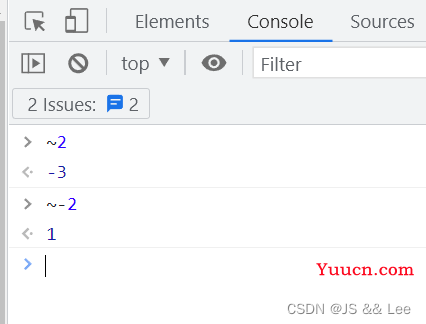
以上方法,非常好用
顺便给大家介绍一种JS中最快速取整的方式,就是小数取整数,符号:~~,写法:~~小数
举个例子
~~3.1415926
> 首先对3.1415926进行非运算 --> ~3.1415926 -->取出整数部分3,结果为-4
> 然后再对-4进行非运算 --> ~-4 --> 结果为3但小编并不介意使用这种方法,不太容易阅读,可以拿来炫炫技巧
JS中的异或运算
再给大家介绍一种位运算:异或运算,符号:^ ,写法:数字1 ^ 数字2
异或运算:将数字1和数字2按32位二进制进行比较,不同为1,相同为0
举个例子 1 ^ 2
1 ^ 2
1 对应的二进制是 --> 0000 0000 0000 0000 0000 0000 0000 0001
2 对应的二进制是 --> 0000 0000 0000 0000 0000 0000 0000 0010
由于前30位相比较全部为0,这里就比较后两位
-- 0 1 --
-- 1 0 --
---------
-- 1 1 -- // 二进制补齐32位,转换成十进制后,结果为3炫技的时刻又到啦!!!
如果面试官问你交换变量的方法,你能写出来几种
小编给大家带来下面几种方法
let a = 1,b = 2;
//方式一
let temp = a;
a = b;
b = temp;
console.log(a,b) //输出2 1
//方式二
a = a + b;
b = a - b;
a = a - b;
console.log(a,b) //输出2 1
//方式三
a = a ^ b;
b = a ^ b;
a = a ^ b;
console.log(a,b) //输出2 1介绍完JS中的位运算,相信大家都不陌生了,那么位运算到底应用于JS中的那些场景呢?
JS中位运算的应用场景
这里小编给带来,js中位运算的常见场景
位的叠加(开关)
举个例子
//管理所有权限
let AllPermission = {
read:0b001, //读权限
write:0b010, //修改权限
create:0b100, //创建权限
}
//权限1表示可读可写
let permission1 = AllPermission.read | AllPermission.write
//判断权限:权限1中是否有可读权限
permission1 & AllPermission === AllPermission ? console.log("可读") : console.log("不可读")
//输出可读JS中的位移运算
接下来给大家介绍一下js中的位移运算,包含左位移和右位移
左位移
符号:<<
写法:数字1 << 数字2
左位移:将数字1的二进制位(除符号外),左位移数字2的次数
举个例子: 3 << 1
3 << 1
3 对应的二进制是 --> 0000 0000 0000 0000 0000 0000 0000 0011
左移一位后是 --> 0000 0000 0000 0000 0000 0000 0000 0110
左移运算,是整个32位向左移动,最后移动多少位,后面补多少0
所以3 << 1 的结果为 0110 ,转换为十进制为6由上面可以得出左移运算的规律:数字1 乘以 2的数字2次方
3 << 1 = 3 * 2 ^ 1 = 6
右位移
符号: >>
写法:数字1 >> 数字2
右位移:将数字1的二进制位(除符号外),右位移数字2的次数
注意!!!!!------->右位移有可能会丢失精度,请谨慎使用
举个例子 3 >> 1
3 >> 1
3 对应的二进制是 --> 0000 0000 0000 0000 0000 0000 0000 0011
右移一位后是 --> 0000 0000 0000 0000 0000 0000 0000 0001
右移运算,是整个32位向右移动,最后移动多少位,符号位不变,前面补多少0
所以3 >> 1 的结果为 0001 ,转换为十进制为1求右位移的快速方法:
举个例子 5 >> 1
相当于 5 / 2^1 ,然后取整数部分,结果为2
全右位移
符号:>>>
写法:同右位移
全右位移:同右位移,区别在于,符号位会跟着移动
举个例子 -1 >>> 1
-1 >>> 1
-1 对应的二进制是 --> 1111 1111 1111 1111 1111 1111 1111 1110
全右移后是 --> 0111 1111 1111 1111 1111 1111 1111 1111
所以-1 >>> 1 的结果为 0111 1111 1111 1111 1111 1111 1111 1111 ,转换为十进制为2147483647好啦,今天的JS位运算已经全部介绍完毕,你学会了吗