一、数据处理
1.1 数据集介绍
本实验使用波士顿房价预测数据集,共506条样本数据,每条样本包含了13种可能影响房价的因素和该类房屋价格的中位数,各字段含义如下表所示:
| 字段名 | 类型 | 含义 |
|---|---|---|
| CRIM | float | 该镇的人均犯罪率 |
| ZN | float | 占地面积超过25,000平方呎的住宅用地比例 |
| INDUS | float | 非零售商业用地比例 |
| CHAS | int | 是否邻近 Charles River 1=邻近;0=不邻近 |
| NOX | float | 一氧化氮浓度 |
| RM | float | 每栋房屋的平均客房数 |
| AGE | float | 1940年之前建成的自用单位比例 |
| DIS | float | 到波士顿5个就业中心的加权距离 |
| RAD | int | 到径向公路的可达性指数 |
| TAX | int | 全值财产税率 |
| PTRATIO | float | 学生与教师的比例 |
| B | float | 1000(BK-0.63)^2,其中BK是城镇中黑人的比例 |
| LSTAT | float | 低收入人群占比 |
| MEDV | float | 同类房屋价格的中位数 |
数据集下载地址:https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data
1.2 数据导入
(1)波士顿房价预测数据集存储在文本文件中的数据格式为下图所示:
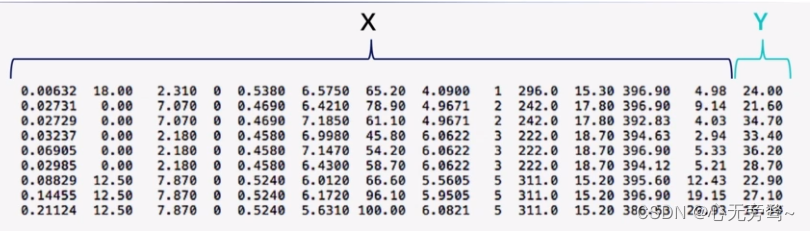
其中的X就是数据集介绍中的CRIM-LSTAT部分,而Y就是MEDV,即同类房屋价格的中位数,也就是我们后面要预测的值。
(2)使用Numpy从文件导入数据np.fromfile
# 导入需要用到的package
import numpy as np
import json
# 读入训练数据
datafile = 'housing.data'
data = np.fromfile(datafile, sep=' ')
导入结果:

注释: np.tofile和np.fromfile可以实现数组写到磁盘文件中
print(data.shape)
# 输出(7084,)
我们可以发现,我们进行上述代码操作以后,将文件中的数据集生成了一个一维的数组,通过打印data.shape可以发现这个一维数组的长度为7084。
细心的朋友不难发现,7084不就是506 x 14以后的结果吗~
没错,在这时候我们就需要重新将data数据重新处理一下,用reshape()方法将其处理为(506, 14)的二维数组。
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
feature_num = len(feature_names)
# 将原始数据进行reshape, 变为[N, 14]这样的形状
data = data.reshape([data.shape[0] // feature_num, feature_num])
print(data.shape)
# 输出(506, 14)
# 查看数据
X = data[0]
print(X.shape)
print(X)
# 输出
#(14,)
# [6.320e-03 1.800e+01 2.310e+00 0.000e+00 5.380e-01 6.575e+00 6.520e+01
# 4.090e+00 1.000e+00 2.960e+02 1.530e+01 3.969e+02 4.980e+00 2.400e+01]
由此可以看出每条数据是一个长度为14的一维数组,前13项是影响房价的因素,最后一项是房价。
1.3 数据集划分
在机器学习和深度学习过程中,往往要将数据集划分为训练集和测试集两部分,训练集用来进行训练,一般会取数据集的80%-90%,而测试集用来对训练好的模型性能进行评估,一般只取少量数据集,大概为10%左右。
ratio = 0.8
offset = int(data.shape[0] * ratio)
train_data = data[:offset]
test_data = data[offset:]
print(train_data.shape)
print(test_data.shape)
# 输出:
# (404, 14)
# (102, 14)
波士顿房价预测数据集中原有数据集为506行,经过划分以后,训练集为原来的80%,即404,测试集为原来的20%,即102。
1.4 归一化处理
对特征取值范围进行归一化,有两个好处:
- 特征训练更高效
- 特征前的权重大小可代表该变量对预测结果的贡献度
注意:预测时,样本数据同样也需要归一化,以训练样本的均值和极值计算
# 计算train数据集的最大值、最小值和平均值
maxinums, mininums, avgs = data_slice.max(axis=0), data_slice.min(axis=0), data_slice.sum(axis=0) / data_slice.shape[0]
# 对数据进行归一化处理
for i in range(feature_num):
# print(maxinums[i], mininums[i], avgs[i])
data[:, i] = (data[:, i] - avgs[i]) / (maxinums[i] - mininums[i])
1.5 将完整代码封装成load_data函数
def load_data():
# 从文件导入数据
datafile = 'housing.data'
data = np.fromfile(datafile, sep=' ')
print(data.shape)
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
feature_num = len(feature_names)
# 将原始数据进行reshape, 变为[N, 14]这样的形状
data = data.reshape([data.shape[0] // feature_num, feature_num])
print(data.shape)
X = data[0]
print(X.shape)
print(X)
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
data_slice = data[:offset]
# 计算train数据集的最大值、最小值和平均值
maxinums, mininums, avgs = data_slice.max(axis=0), data_slice.min(axis=0), data_slice.sum(axis=0) / data_slice.shape[0]
# 对数据进行归一化处理
for i in range(feature_num):
# print(maxinums[i], mininums[i], avgs[i])
data[:, i] = (data[:, i] - avgs[i]) / (maxinums[i] - mininums[i])
# 训练集和测试集的划分比例
# ratio = 0.8
train_data = data[:offset]
test_data = data[offset:]
return train_data, test_data
1.6 获取数据
# 获取数据
train_data, test_data = load_data()
print(train_data.shape)
x = train_data[:, :-1]
y = train_data[:, -1:]
print(x[0])
print(y[0])
#[-0.02146321 0.03767327 -0.28552309 -0.08663366 0.01289726 0.04634817
# 0.00795597 -0.00765794 -0.25172191 -0.11881188 -0.29002528 0.0519112
# -0.17590923]
#[-0.00390539]
二、设计模型
波士顿房价预测案例是一个非常典型的线性回归问题。
2.1 前向计算
输入x一共有13个变量,y只有1个变量,所以权重w的shape是[13, 1]
- w可以任意赋初值如下
w = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, -0.1, -0.2, -0.3, -0.4, 0.0]
w = np.array(w).reshape([13, 1])
- 取出第1条样本数据,观察它与w相乘之后的结果
x1 = X[0]
t = np.dot(x1, w)
print(t)
# 输出:[0.03395597]
- 另外还需要初始化权重b,这里我们给它赋值-0.2观察输出
b = -0.2
z = t + b
print(z)
# 输出 [-0.16604403]
2.2 以类的方式实现网络结果(前向计算)
- 使用时可以生成多个模型示例
- 类成员变量有w和b,在类初始化函数时初始化变量(w随机初始化,b = 0)
- 函数成员forward 完成从输入特征x到输出z的计算过程(即前向计算)
class NetWork(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置了固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
随机选取一个样本测试下效果
net = NetWork(13)
x1 = x[0]
y1 = y[0]
z = net.forward(x1)
print(z)
# 输出 [-0.63182506]
此时我们可以看出,现阶段搭建的模型只有一个花架子,并不具备预测的能力,所以还需改进。
三、模型的损失与优化
3.1 模型好坏的衡量指标——损失函数(loss function)
在回归问题中均方误差是一种比较常见的形式,分类问题中通常会采用交叉熵损失函数,后续有机会再给大家讲解,咱们这篇文章主要讲解均方误差。

3.2 训练配置—同时计算多个样本的损失函数
在训练过程中,我们要计算所有样本的损失,而不是单个样本的损失。

在此过程中我们用到了Numpy的广播机制,便捷的实现多样本的计算
广播功能:像使用单一变量一样操作数组。
class NetWork(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置了固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
cost = error * error
cost = np.mean(cost)
return cost
net = NetWork(13)
x1 = x[0:3]
y1 = y[0:3]
z = net.forward(x1)
print('predict', z)
loss = net.loss(z, y1)
print('loss', loss)
# 输出
# predict [[-0.63182506]
# [-0.55793096]
# [-1.00062009]]
# loss 0.7229825055441156

方案1:
我们在高中的时候就学习过,当一条曲线处于极值点的时候,斜率为0,即导数为0。那么我们就可以根据上图中的导数方程来求解出参数w和b的值,以此来达到损失函数极小值的目的。但是由于并不是所有的函数都是像均方误差这样可逆的,在我们进行机器学习或者深度学习的过程中,遇见最多的就是不可逆函数,不可逆函数简单举个例子就是有一个y=x的方程,我们可以根据y求导解出x,但是却不能根据x求导解出y。也就是说不能反过来求解,这就是不可逆函数。
方案2:
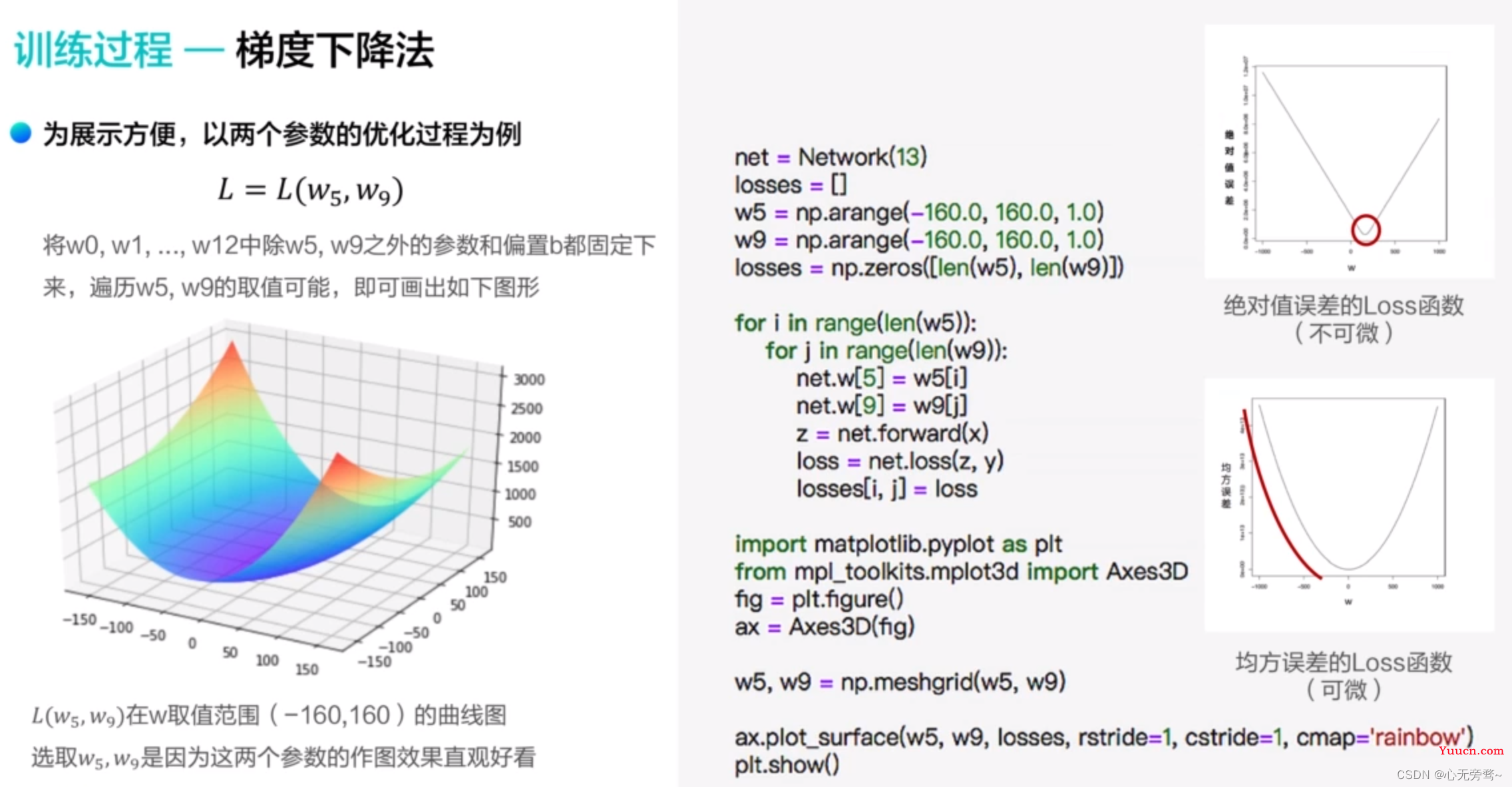
在梯度下降法中,根据上图我们可以理解为什么我们使用均方误差而不是绝对误差,我们可以看到,绝对值误差画出来的图像没有坡度,是不可微的,而均方误差画出的Loss函数图像可以看出是可微的,这样子就可以让我们在求解过程中更加的方便。
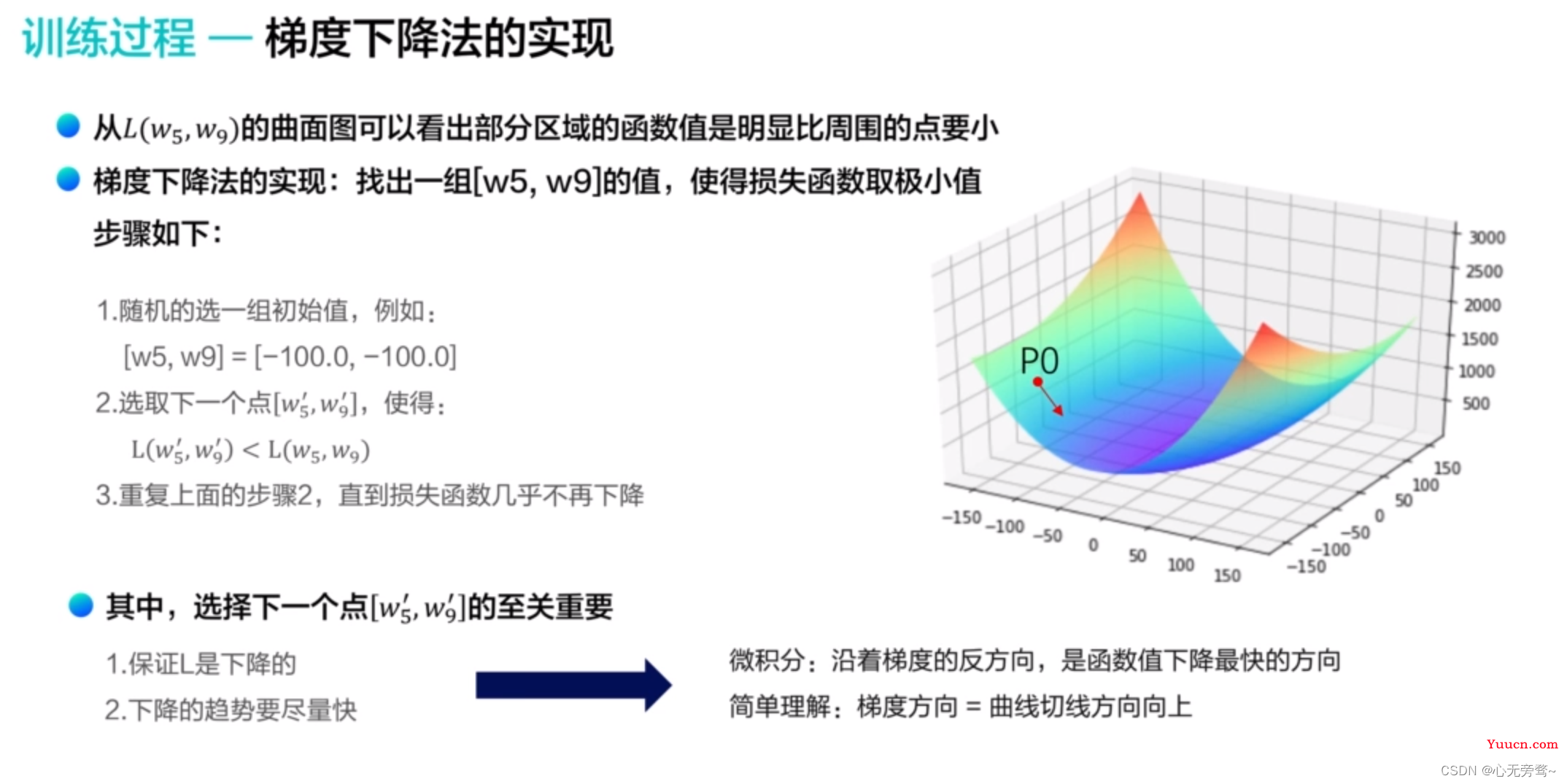
沿着梯度的反方向可以理解为沿着切线方向下降速度最快的方向,一般切线方向都是向上的,而反方向就是向下的方向。
四、梯度下降代码实现
4.1 训练过程—计算梯度的公式推导
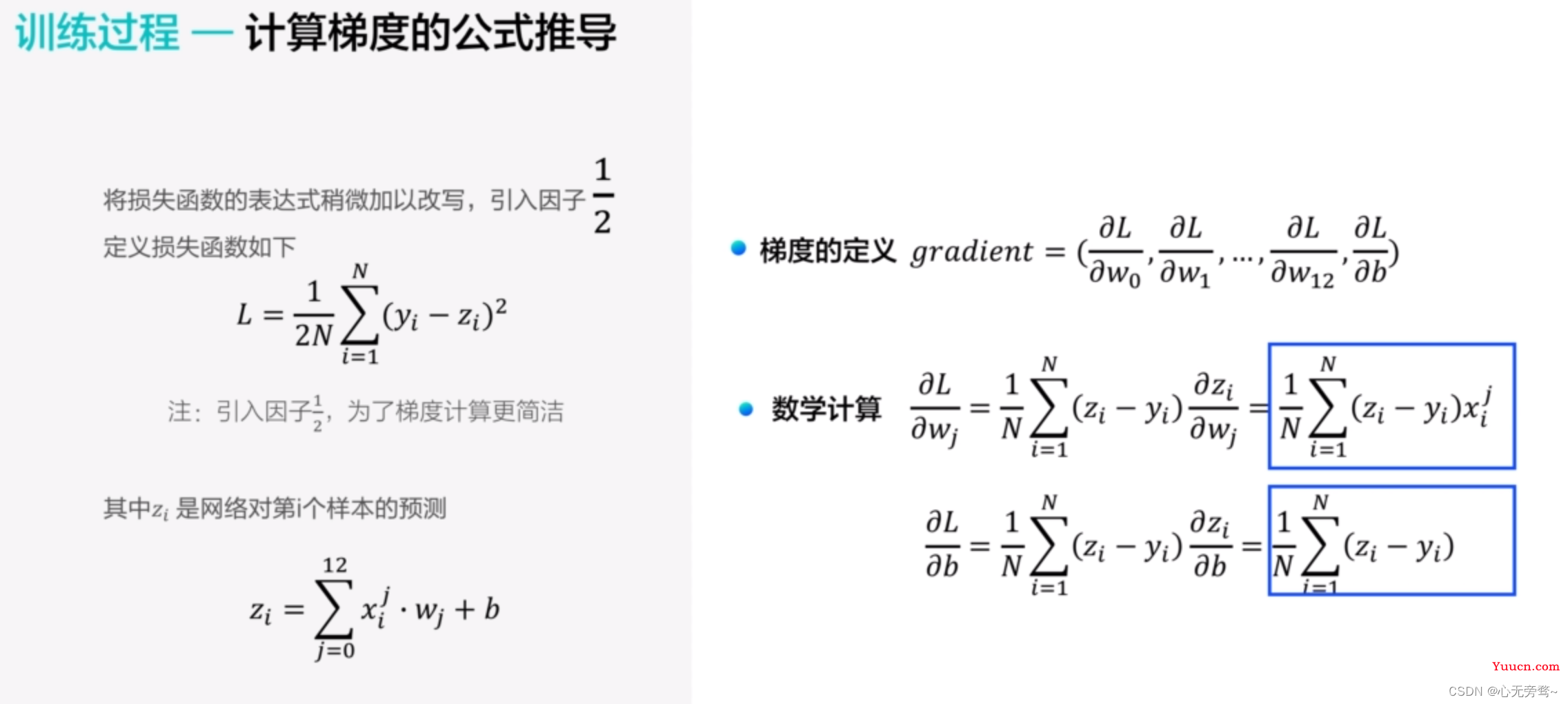
我们在进行梯度公式的推导之前,引入了1/2的因子,这样做的目的仅仅是为了我们的推导过程更加的简洁,没有别的目的,而且这样做并不影响我们整体的推导过程。
4.1.1 训练过程—计算梯度的公式推导(一个样本)
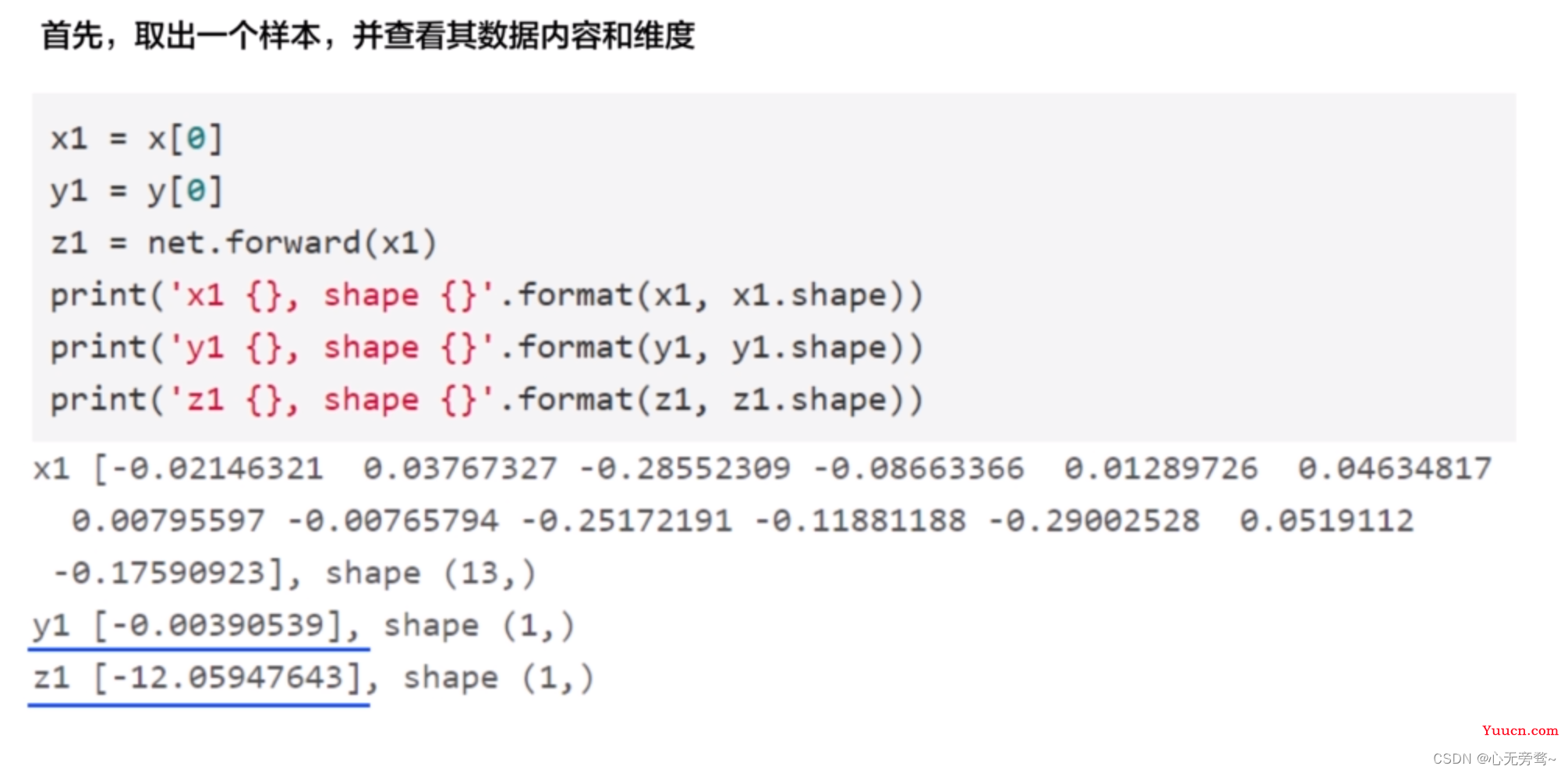

4.1.2 训练过程—基于Numpy广播机制进行梯度计算(多个样本)
-
基于Numpy的广播机制,扩展参数的维度
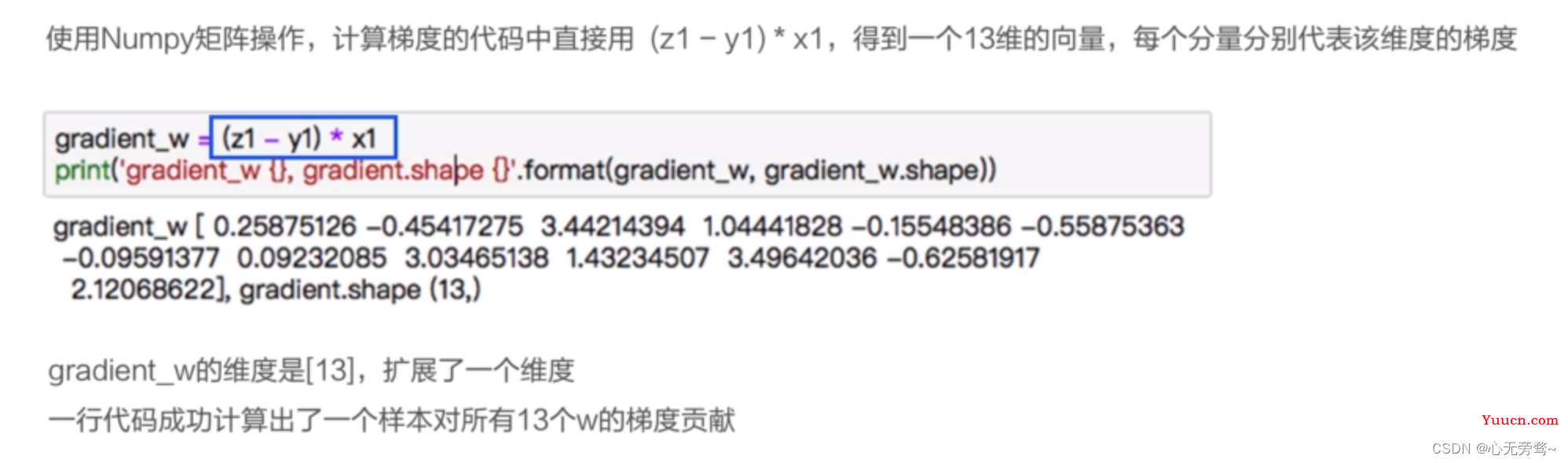
4.1.3 训练过程—基于Numpy计算单个样本—>多个样本对梯度的贡献
- 同样,基于Nupy的广播机制,扩展样本的维度
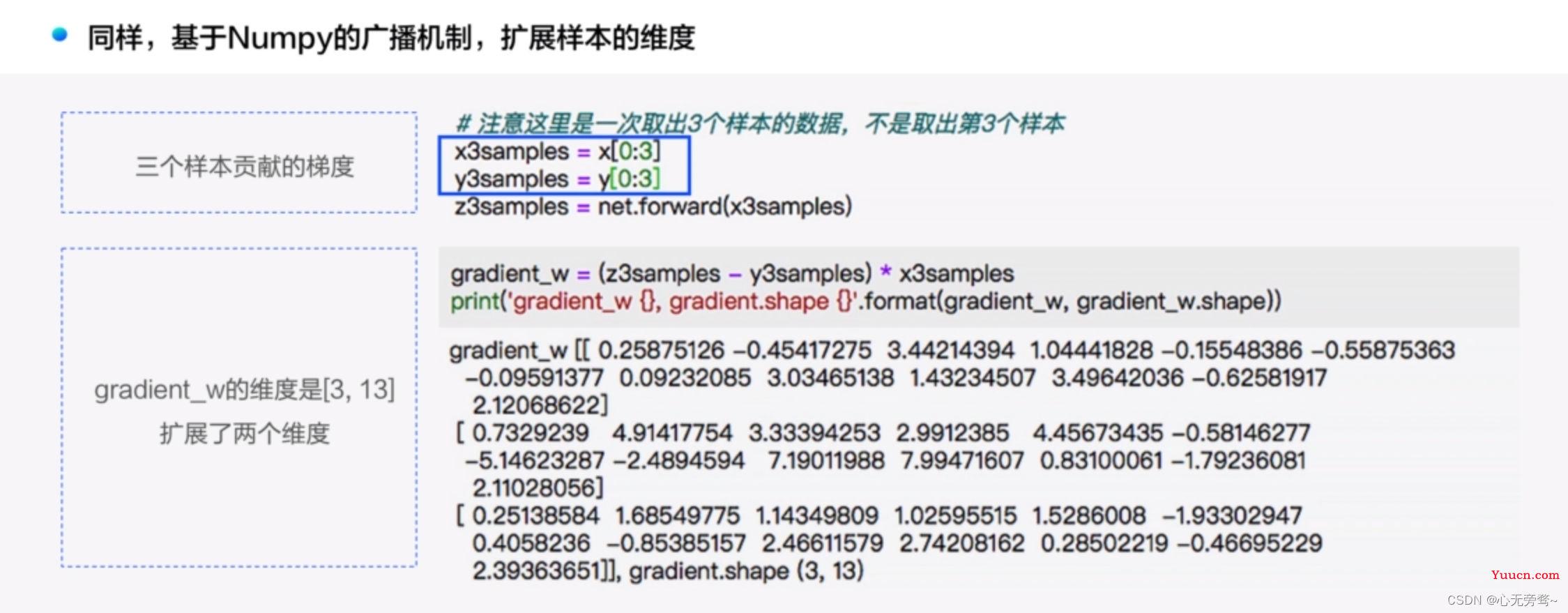
4.1.4 训练过程—计算所有样本对梯度的贡献,代码十分简洁
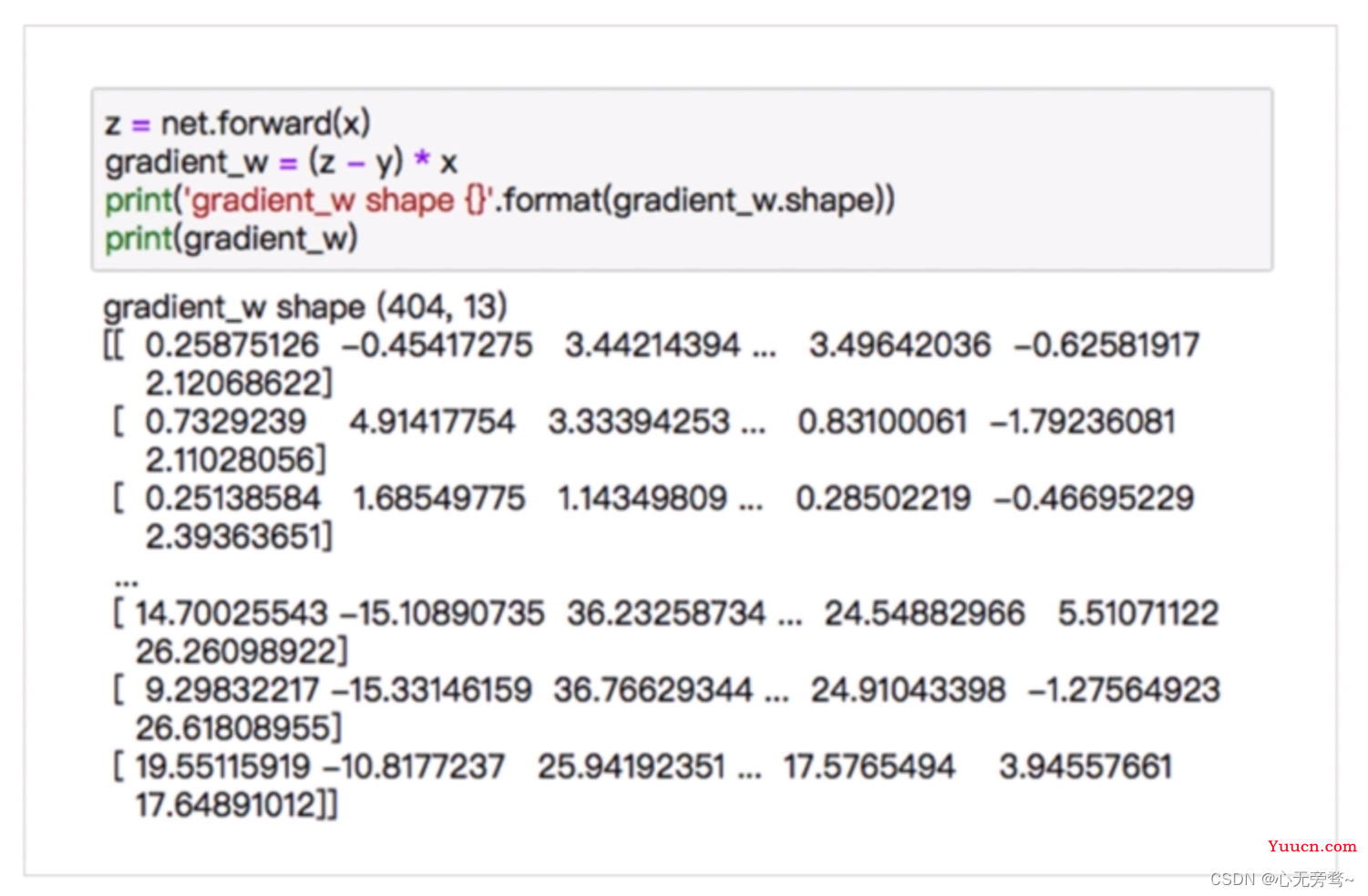
4.4.5 训练过程—所有样本对梯度的贡献取平均值
-
参数的更新方向要考虑所有样本的“意见”,总的梯度是所有样本对梯度贡献的平均值
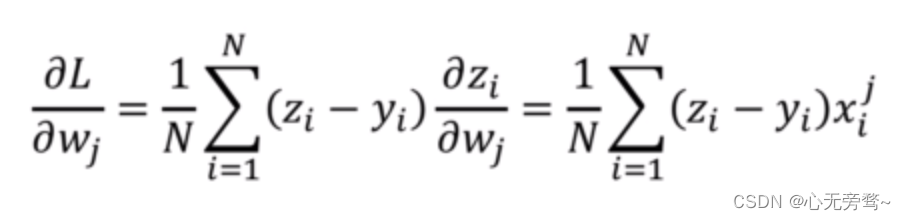
-
使用Numpy里面的矩阵操作来完成此过程:

因为后续每走一小步都要进行维度的相加,所以(13, )要加上1维,变成(13,1),使得到梯度的维度和参数的维度一致,但是加上的1维相当于是虚的,因为13 x 1与13是一样的数字。
4.2 前向计算和后向传播的完整代码
- 全流程的步骤
1.前向计算
2.拿到1(前向计算的结果),才能计算损失
3.拿到1和2,才能计算梯度
4.根据3,更新参数值
注意:其中第4步是反复循环进行的。
class NetWork(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置了固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
cost = error * error
cost = np.mean(cost)
return cost
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z - y) * x
gradient_w = np.mean(gradient_w, axis=0) # axis=0表示把每一行做相加然后再除以总的行数
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
# 此处b是一个数值,所以可以直接用np.mean得到一个标量(scalar)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta=0.01): # eta代表学习率,是控制每次参数值变动的大小,即移动步长,又称为学习率
self.w = self.w - eta * gradient_w # 相减: 参数向梯度的反方向移动
self.b = self.b - eta * gradient_b
def train(self, x, y, iterations=1000, eta=0.01):
losses = []
for i in range(iterations):
# 四步法
z = self.forward(x) # 前向计算
L = self.loss(z, y) # 求误差
gradient_w, gradient_b = self.gradient(x, y) # 求梯度
self.update(gradient_w, gradient_b, eta) # 更新参数
losses.append(L)
if (i + 1) % 10 == 0:
print('iter {}, loss {}'.format(i, L))
return losses
五、完整代码
import numpy as np
from matplotlib import pyplot as plt
def load_data():
# 从文件导入数据
datafile = 'housing.data'
data = np.fromfile(datafile, sep=' ')
print(data.shape)
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
feature_num = len(feature_names)
# 将原始数据进行reshape, 变为[N, 14]这样的形状
data = data.reshape([data.shape[0] // feature_num, feature_num])
print(data.shape)
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
data_slice = data[:offset]
# 计算train数据集的最大值、最小值和平均值
maxinums, mininums, avgs = data_slice.max(axis=0), data_slice.min(axis=0), data_slice.sum(axis=0) / data_slice.shape[0]
# 对数据进行归一化处理
for i in range(feature_num):
# print(maxinums[i], mininums[i], avgs[i])
data[:, i] = (data[:, i] - avgs[i]) / (maxinums[i] - mininums[i])
# 训练集和测试集的划分比例
# ratio = 0.8
train_data = data[:offset]
test_data = data[offset:]
return train_data, test_data
class NetWork(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置了固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
cost = error * error
cost = np.mean(cost)
return cost
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z - y) * x
gradient_w = np.mean(gradient_w, axis=0) # axis=0表示把每一行做相加然后再除以总的行数
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
# 此处b是一个数值,所以可以直接用np.mean得到一个标量(scalar)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta=0.01): # eta代表学习率,是控制每次参数值变动的大小,即移动步长,又称为学习率
self.w = self.w - eta * gradient_w # 相减: 参数向梯度的反方向移动
self.b = self.b - eta * gradient_b
def train(self, x, y, iterations=1000, eta=0.01):
losses = []
for i in range(iterations):
# 四步法
z = self.forward(x)
L = self.loss(z, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(L)
if (i + 1) % 10 == 0:
print('iter {}, loss {}'.format(i, L))
return losses
# 获取数据
train_data, test_data = load_data()
print(train_data.shape)
x = train_data[:, :-1]
y = train_data[:, -1:]
# 创建网络
net = NetWork(13)
num_iterations = 2000
# 启动训练
losses = net.train(x, y, iterations=num_iterations, eta=0.01)
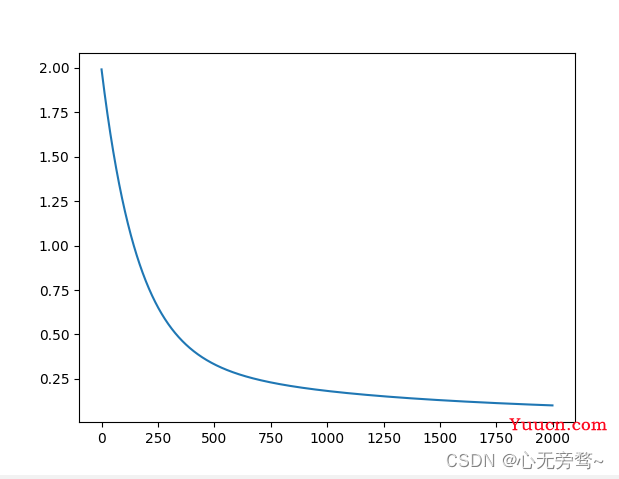
# 画出损失函数的变化趋势
plot_x = np.arange(num_iterations)
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()
训练结果: