机器学习中的隐变量/潜变量和隐藏空间/潜在空间
-
- 1.什么是隐变量?
- 1.什么是潜在空间(Latent Space)?
- 2.机器学习中为什么要压缩数据?
- 3.潜在空间中的“空间”是什么意思?
- 4.数据相似的相似是什么意思?
1.什么是隐变量?
在统计学中,隐变量或称潜变量,潜在变量,与观测变量相对,指的是不可观测的随机变量。潜变量可以通过使用数学模型依据观测得的数据被推断出来。用潜在变量解释观测变量的数学模型称为潜变量模型。 有些情况下,潜变量和现实中的一些因素是有关系的。测量这些因素理论上可行,实际上却很困难。这些情况里通常使用“隐变量(hidden variables)”这个词。另外一些情况下,潜变量指的是抽象概念,例如分类、行为、心理状态、数据结构等等。在这些情况下人们用 hypothetical variables 或者 hypothetical constructs 指代潜变量。
使用潜变量的好处之一是潜变量能用来降低数据的维度。大量的观测变量能够被整合起来成为一个潜变量来表示深层次的概念,使得观测数据更容易理解。
1.什么是潜在空间(Latent Space)?
如果必须用一句话来描述潜在空间,它仅仅意味着压缩数据的表示。

上图是手写数字(0-9)的大数据集。同一个数字3的手写图像与不同数字的图像7两者是最相似的。我们能否训练一种算法来识别这些相似性呢?如何做到呢?
如果你已经训练了一个模型来对数字进行分类,那么这个模型已经学到了图像之间的 “结构相似性”。事实上,这就是模型为什么能够对数字进行分类–通过学习每个数字的特征。
但模型学到每个数字的特征这个过程对你来说是“隐藏的”。这也就是隐藏/潜在空间中的Latent的意思,“隐藏的”。
“潜在空间”的概念很重要,是“深度学习”的核心。深度学习就是学习数据的特征并简化数据表示,以寻找模型。
2.机器学习中为什么要压缩数据?
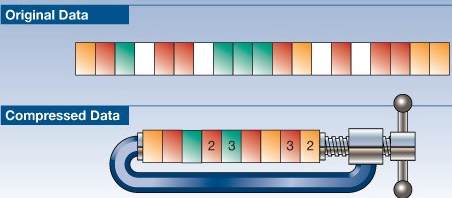
数据压缩(Data compression)被定义为使用比原始表示更少的位来编码信息的过程。比如一共数据点是19D的数据点,即需要19个值来定义唯一点,然后将所有这些信息压缩到一个9D数据点中。如下图所示:
通常在机器学习中,数据被压缩以学习有关数据点的重要信息。例如,假设我们想使用全卷积神经网络(FCN)训练一个模型来对图像进行分类,即给定数字的图像后对输出相应的数字。在模型“学习”过程中,它只是简单地学习每一层的特征(边、角度等),并将这些特征组合到特定的输出中。
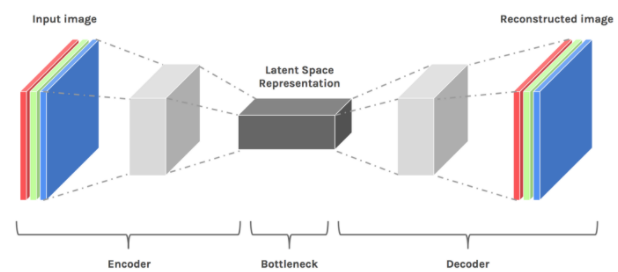
但每次模型通过一个数据点学习时,图像的维数首先会降低,然后才会增加。(如下图中的编码器和瓶颈层Bottleneck)。当降维时,我们认为这是一种有损压缩。
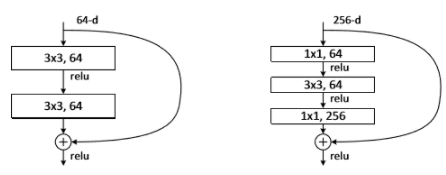
Bottleneck layer又称之为瓶颈层,使用的是1x1的卷积神经网络。之所以称之为瓶颈层,是因为长得比较像一个瓶颈,即中间比较细。使用 1x1 网络的一大好处就是可以大幅减少计算量。
由上图可以看到,输入和输出的通道数是相同的都是256,但block结构里面的通道数先是64,是小于输入输出的通道数的。
有损压缩:有损数据压缩(英语:lossy compression)是一种数据压缩方法,经过此方法压缩、解压的数据会与原始数据不同但是非常接近。它是与无损数据压缩相对的压缩方法。有损数据压缩又称破坏性资料压缩、有损压缩、不可逆压缩。有损数据压缩借由将次要的数据舍弃,牺牲一些质量来减少数据量、提高压缩比。
因为模型需要重建压缩数据(见解码器),它必须学会存储所有相关信息,忽略噪声。这就是压缩的价值所在——它可以让我们去掉任何无关的信息,只关注最重要的特性。
这个“压缩状态”是我们数据的潜在空间表示。
3.潜在空间中的“空间”是什么意思?
压缩的数据好像跟空间毫无关联,但两者有相似的地方。
假设我们的原始数据集是尺寸为5 x 5 x 1的图像。我们将我们的潜在空间维数设为3 x 1,这意味着我们的压缩数据点是一个三维的向量。
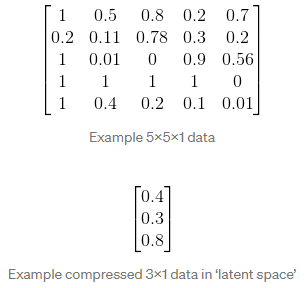
现在,每个压缩数据点仅由3个数字唯一定义。这意味着我们可以在3D空间上绘制这些数据(一个数字是x,另一个是y,另一个是z)。这就是我们所说的“空间”。
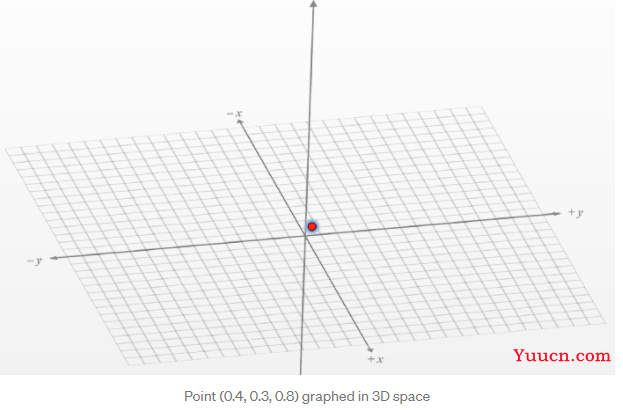
当我们绘制潜在空间中的点时,我们可以把它们想象成空间中的坐标,在这个坐标中,“相似”的点在图上更接近。
那么现在的问题是,一般潜在空间的表示往往不是2维或3维向量,因为会丢失太多的信息。那对于空间中的四维点或n维点,甚至非向量我们如何想象呢?
答案是,我们不能。我们是三维生物,无法理解n维空间(比如n > 3)。然而,有一些工具,如t-SNE,可以将我们的高维潜在空间表示转换成我们可以可视化的表示(2D或3D)。(见下面可视化潜在空间部分。)
什么又是“相似”的图像,为什么我们数据的维度降低会使相似的图像在空间中“更接近”?
4.数据相似的相似是什么意思?
举个例子,如果我们看下面三张图片-两张椅子和一张桌子,我们很容易地会说两张椅子的图片是最相似的,而桌子是最不同于任何一张椅子的图片。

是什么让这两个椅子图像“更相似”呢?因为椅子与桌子相比有不同的特点(如靠背,没有抽屉,腿之间的连接)。这些都可以通过我们的模型通过学习边、角等模式来“学习”出来。如前所述,这些特征会被打包在数据的潜在空间表示中。
因此,随着维数的降低,每个图像不同的“多余的”信息(例如椅子颜色)会从潜在空间表示中被“移除”,因为每个图像只有最重要的特征被存储在潜在空间表示中。
因此,当我们降低维度时,这两个椅子的模型表示变得更相似。如果我们想象它们在同一个空间,它们挨得更近。
==注意:==在整篇文章中提到的“更近”是一个模糊的概率,并不是一个确定的欧几里得距离。
参考自Understanding Latent Space in Machine Learning