
本博客封面由
ChatGPT + Midjourney共同创作而成。
文章目录
-
- 前言
- 1. 算法思想
- 2. 细节梳理
-
- 2.1 DAN编码
- 2.2 种群初始化及超参选择
- 2.3 适应度函数
- 2.4 选择、交叉(交配)与变异
- 2.5 终止条件
- 3. 算法实现
-
- 3.1 问题场景
- 3.2 从遗传算法角度分析
- 3.3 python实现
- 代码仓库:IALib[GitHub]
前言
本篇是智能算法(Python复现)专栏的第一篇文章,主要介绍遗传算法(Genetic Algorithm, GA)的思想,python实现及相关应用场景模拟。
生物在自然界的生存繁衍,经历了一代又一代的更替,新旧物种的淘汰或进化展示了生物在自然界的自适应能力。受此启发,遗传算法模拟生物遗传和进化过程,成为求解极值问题的一类自组织、自适应的人工智能技术。其理论来源包括拉马克进化学说(Lamarckism)、达尔文进化学说和孟德尔遗传学(Mendelian inheritance),主要借鉴的生物学基础是生物的遗传、变异和进化。
1. 算法思想
遗传算法是进化算法(Evolutionary Algorithms, EA)的一个分支,将达尔文的进化理论引入计算机。具体可以表述为:首先根据某种机制创建初始种群,对初始种群进行适应度(fitness)评估,保留初始种群中最优适应度解作为当前最优解。然后对种群中的个体进行选择(select)、交叉(crossover)和变异(mutation),得到新的种群,若新种群中的最优解优于父代的最优解,则替换。重复上述操作,直到满足算法终止条件。
种群中的每个个体代表问题的一种解。
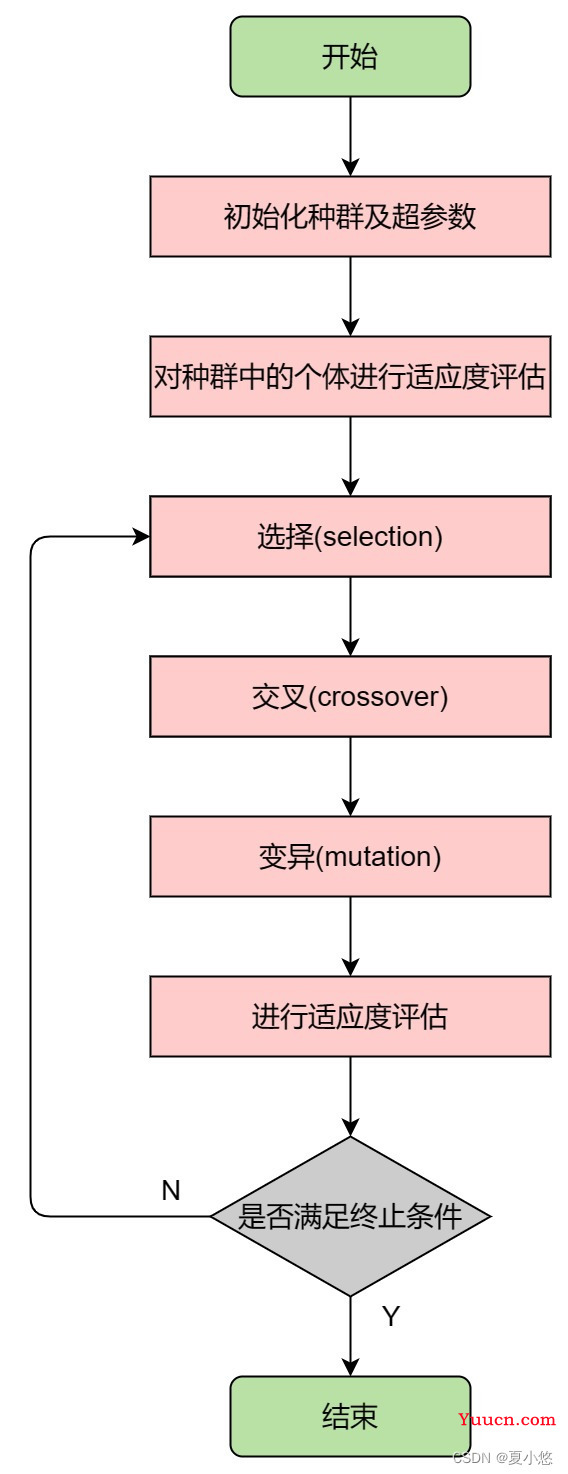
根据遗传算法的流程图,我们可以梳理出5个问题,对应着遗传算法的5个组成部分:
(1) 问题的解如何进行编码,即DNA编码?
(2) 种群的初始化如何进行?超参数如何选择?
(3) 适应度函数如何设计?
(4) 如何对DNA编码进行选择、交叉和变异?
(5) 终止条件是什么?
2. 细节梳理
2.1 DAN编码
解的遗传表示称为遗传编码,因为遗传算法不能直接处理问题空间的决策变量,必须转换成由基因按一定结构组成的染色体,所以就有了编码操作,反之将编码空间向问题空间的映射称为译码。
编码的方式有很多种,根据采用的符号,可以分为二进制编码、实数编码和整数编码等;根据编码采用的结构,可以分为一维编码和多维编码;根据编码采用的长度,可以分为固定长度的编码和可变长度的编码。对于不同的优化问题,要选择合适的编码方式,但应该遵循以下约束:
(1) 不冗余性:从编码到解码的映射是1对1的;
(2) 合法性:对编码的任意排列都对应着一个解;
(2) 完备性:任意解都对应着一个编码。
2.2 种群初始化及超参选择
产生初始种群的方法通常有两种:一种是由完全随机的方法产生的,它适合于对问题的解无任何先验知识的情况;另一种是根据某些先验知识转变为必须满足的一组要求,然后在满足这些要求的解中再随机地选取样本。就目前工作中所使用的情况来看,都是随机初始种群。
参数大小的选择对遗传算法执行的结果有很大影响,好的参数设置会加速算法收敛到全局最优解,反之,差的参数选择将会使结果得到局部最优解,甚至会导致结果无法收敛。一般地,需要设置的参数有以下几种:
(1) 种群规模N影响算法的搜索能力和运行效率,一般设置为20~100。N设置较大时,一次所覆盖的模式较多,增大了种群多样性和算法搜索能力,但也增加了计算量,降低了算法运行效率;N设置较小时(群体内个体的多样性减小),容易造成局部收敛;
(2) DNA长度L影响算法的计算量和交配变异操作的效果。L的设置一般由问题定义的解的形式和选择的编码方式决定;
(3) 交叉(交配)概率Pc决定了进化过程中种群内参加交配的染色体的平均数目,取值一般为0.4~0.99,也可以使用自适应方法在算法运行过程中调整交配概率;
(4) 变异概率Pm决定了进化过程中全体发生变异基因的平均个数,取值一般为0.001~0.1。变异操作增加了群体进化的多样性,但Pm值不宜过大,否则会对已找到的较优解有一定的破坏作用,使搜索状态倒退回原来较差的情况。
(5) 在终止条件中,需要设定的有最大进化代数和收敛误差值。最大进化代数一般可设为100~1000,需要根据实际问题来设定,合理的进化代数可以防止算法因不收敛而一直运行。
2.3 适应度函数
适应度函数(fitness function),也叫评价函数。顾名思义,就是用来评价个体的适应度值,适应度值越大的个体越符合算法对解的要求,所以评价函数至关重要,指引解进化的方向。同时,适应度函数的选择会直接影响遗传算法的收敛速度以及能否找到全局最优解。
2.4 选择、交叉(交配)与变异
选择操作的原理本质上是基于达尔文的自然选择学说,它的作用是将遗传搜索引导到搜索空间中有前途的区域。通常采用的选择方法有轮盘赌选择(roulette wheel selection)、锦标赛选择(tournament selection)、随机选择(stochastic sampling)、确定性选择(deterministic sampling)和混合选择(mixed sampling)。
所谓交叉是指把两个父代个体的部分结构加以替换生成新个体的操作,这样可以提高搜索力。在交叉运算之前必须对群体中的个体进行配对。目前常用的配对策略是随机配对,即将群体中的个体以随机方式两两配对,交叉操作是在配对个体之间进行的。
变异就是将染色体编码串中的某些基因用其他的基因来替换。它是遗传算法中不可缺少的部分,目的就是改善遗传算法的局部搜索能力,维持群体的多样性,防止出现早熟现象。设计变异算子需要确定变异点的位置和基因值的替换,最常用的是基本位变异,它只改变编码串中个别位的基因值。从概率上来看,变异发生的概率较小,发挥作用比较慢,效果不明显。
2.5 终止条件
遗传算法终止条件通常有两种:一是设定迭代次数,当算法迭代次数达到设定值时,算法停止;二是当解的变化小于某一设定的较小值时,认为结果收敛,算法停止。使用时可以只使用一种,也可以两种同时使用。
3. 算法实现
3.1 问题场景
最值问题,求解
f
(
x
)
=
x
s
i
n
(
5
x
)
−
x
c
o
s
(
2
x
)
f(x) = xsin(5x) - xcos(2x)
f(x)=xsin(5x)−xcos(2x)在定义域[0, 5]上的最大值。我们先手动计算一下:
f
′
(
x
)
=
2
x
s
i
n
(
2
x
)
+
s
i
n
(
5
x
)
−
c
o
s
(
2
x
)
+
5
x
c
o
s
(
5
x
)
f^\prime (x) = 2 x sin(2 x) + sin(5 x) - cos(2 x) + 5 x cos(5 x)
f′(x)=2xsin(2x)+sin(5x)−cos(2x)+5xcos(5x) 令
f
′
(
x
)
=
f^\prime (x) = 0
f′(x)=0之后,理论上可以求得驻点,但又不太好计算。。。
3.2 从遗传算法角度分析
从上述的公式可以知道,问题的解,也就是最大值对应的变量x是一个浮点数,这里采用二进制编码的方式,具体示例为:
假设定义域内的一个解为1.5,基因编码长度为10,则将转为中间值为307(取整),进一步将其转为二进制为0100110011,同理,也可以将二进制转为真实解,1011111011转为中间值为763,进一步转为浮点数(解)为3.7292277614858262。基因编码与解的关系为:
x
∗
=
i
n
t
(
d
n
a
,
2
)
2
l
e
n
(
d
n
a
)
−
1
×
x
r
a
n
g
e
x^* = \frac {int(dna, 2)} {2^{len(dna)}-1} \times x_{range}
x∗=2len(dna)−1int(dna,2)×xrange
既然是解决最大值问题,那么可以直接将函数
f
(
x
)
f(x)
f(x)直接作为适应度函数,即函数值就表示适应度的值,函数值越大,表示种群个体对环境的适应性越强,就说明种群对应的DNA是最优的(解)。
物竞天择,适者生存。select操作当然是选择适应度较强的个体了,本篇中的crossover操作和mutation操作都采用随机的方式来产生新的种群个体。
3.3 python实现
-*- coding:utf-8 -*-
# Author: xiayouran
# Email: youran.xia@foxmail.com
# Datetime: 2023/3/10 16:55
# Filename: ga.py
import numpy as np
import matplotlib.pyplot as plt
dna_size = 10 # DNA length
population_size = 100 # population size
crossover_rate = 0.7 # mating probability(DNA crossover)
mutation_rate = 0.003 # mutation probability
max_generations = 1000 # maximum iterations
x_range = [0, 5] # x upper and lower bounds
seed = 10086
np.random.seed(seed)
def F(x):
return x*np.sin(5*x) - x*np.cos(2*x) # to find the maximum of this function
# find non-zero fitness for selection
def get_fitness(pred):
return pred + 1e-3 - np.min(pred)
# convert binary DNA to decimal and normalize it to a range(0, 5)
def translateDNA(population):
# 二进制转10进制, 然后归一化, 再乘以x坐标轴
return population.dot(2 ** np.arange(dna_size)[::-1]) / float(2**dna_size-1) * x_range[1]
def selection(population, fitness):
# p: 一维数组, 决定了数组中每个元素采样的概率, 默认为None, 即每个元素被采样的概率相同
# replace=True, 允许元素重复
idx = np.random.choice(np.arange(population_size), size=population_size, replace=True,
p=fitness/fitness.sum())
return population[idx]
def crossover(parent, population):
if np.random.rand() < crossover_rate: # random crossover
i_ = np.random.randint(0, population_size, size=1) # select another individual from population
cross_points = np.random.randint(0, 2, size=dna_size).astype(np.bool) # choose crossover points
parent[cross_points] = population[i_, cross_points] # mating and produce one child
return parent
def mutation(child):
for point in range(dna_size):
if np.random.rand() < mutation_rate: # random mutate
child[point] = 1 if child[point] == 0 else 0
return child
if __name__ == '__main__':
# Step1: initialize the population DNA
population = np.random.randint(2, size=(population_size, dna_size))
fig = plt.figure()
plt.ion() # 交互模式
x = np.linspace(*x_range, 200)
plt.plot(x, F(x))
for _ in range(max_generations):
F_values = F(translateDNA(population))
# something about plotting
if 'sca' in globals():
sca.remove()
sca = plt.scatter(translateDNA(population), F_values, s=100, lw=0, c='red', alpha=0.5)
plt.pause(0.01)
# Step2: compute fitness value
fitness = get_fitness(F_values)
best_id = np.argmax(fitness)
print("Most fitted DNA: {}, x: {}, max_value: {}".format(population[best_id],
translateDNA(population[best_id]),
F(translateDNA(population[best_id]))))
# Step3: selection
population = selection(population, fitness)
population_copy = population.copy()
for parent in population:
# Step4: crossover
child = crossover(parent, population_copy)
# Step5: mutation
child = mutation(child)
parent[:] = child # parent is replaced by its child
plt.ioff()
plt.show()
得到的最优解如下:
Most fitted DNA: [1 1 0 1 0 1 0 1 0 1], x: 4.16911045943304, max_value: 5.738744982619388
模拟过程如下:

代码仓库:IALib[GitHub]
本篇代码已同步至【智能算法(Python复现)】专栏专属仓库:IALib
运行IALib库中的GA算法:
git clone git@github.com:xiayouran/IALib.git
cd examples
python main.py -algo ga