算法题： 一球从100米高度自由落下，每次落地后反跳回原高度的一半

一.序言：

今天在逛C站的时候，突然发现一篇这样的文章《算法题： 一球从100米高度自由落下，每次落地后反跳回原高度的一半》。勾起了我的兴趣（就像小学生看见了加减法的题目，很兴奋，终于可以装13了）。

二.题目：

一球从100米高度自由落下，每次落地后反跳回原高度的一半；再落下，求它在 第10次落地时，共经过多少米？第10次反弹多高？

三.思路：

1.首先我们来看一下这个球的运动轨迹：

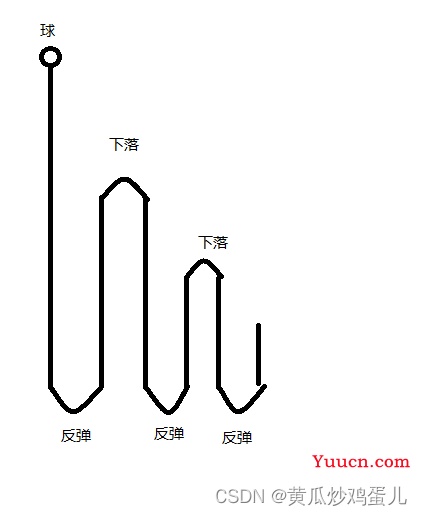
2.解题思路：
我们可以清楚的看到：
a.一次反弹的高度，是原高度的一半：用高度除2循环或者递归所需次数，就能得出最终高度。
b1.经过的路程：球体原来的高度加上反弹的高度，就是一次路程，循环所需次数累加，就是总路程。
b2.经过的路程：除第一次和最后一次的高度都乘2，再加上第一次和最后一次的高度，就是最终路程。
b3.经过的路程：所有的高度都程2，再减去第一次的高度和最后一次的高度，就是最终路程。

以上是没有认真审题时，没看到路程是第10次落地时，不加上反弹路程时的思路。

经过的路程，我比较倾向于b1方案，最符合实际运动轨迹。

四.代码：

1.用球体运动轨迹来计算结果：

 //算法题： 一球从100米高度自由落下，每次落地后反跳回原高度的一半
 //题目：一球从100米高度自由落下，每次落地后反跳回原高度的一半；再落下，求它在 第10次落地时，共经过多少米？第10次反弹多高？
        //最终反弹高度    总共运动路程
        double height = 100,sum = 0;
        //球体运动
        for (int i = 0; i < 10; i++)
        {
            //本次路程
            double the = 0;
            //本次加下落路程
            the += height;
            //累加下落路程
            sum += height;
            //获取本次反弹高度
            height /= 2;
            Console.WriteLine($"第{i + 1}次反跳，高度为：{height}");
            //第10次落地，不用计算反弹高度
            if (i < 9)
            {
                //本次路程累加反弹高度
                the += height;
                //累加反弹路程
                sum += height;
            }
            Console.WriteLine($"第{i + 1}次路程：{the}");
            Console.WriteLine($"{i + 1}次反弹时，总路程：{sum}");
        }
        Console.WriteLine($"答:第10次落地时，共经过{sum}米，10次反弹{height}米");

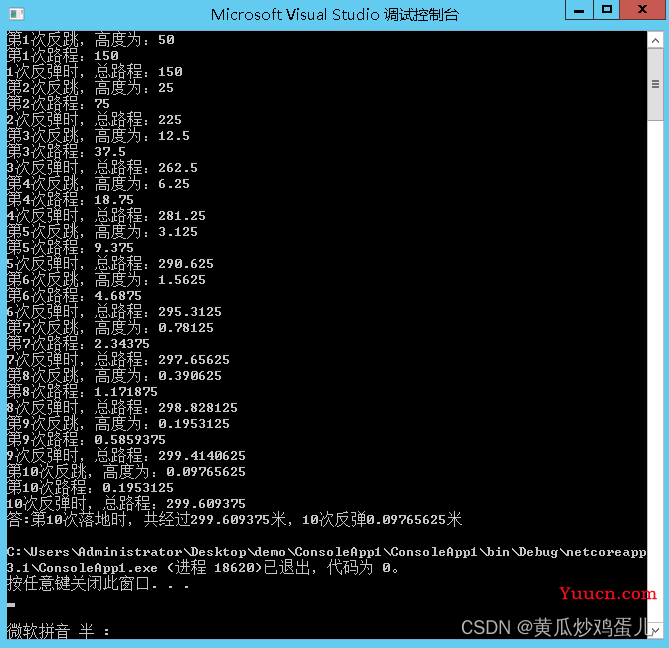
2.用2倍中间路程之后，最后加起始高度计算结果：

        double height = 100, sum = 0;
        for (int i = 0; i < 10; i++)
        {
            //反弹高度
            height /= 2;
            if (i < 9)
            {
                sum += height * 2;
            }
            Console.WriteLine($"第{i + 1}次反跳，高度为：{height}");
            Console.WriteLine($"第{i + 1}次反跳，总路程：{sum}");
        }
        //总路程加上最开始的100米
        sum +=  100;
        Console.WriteLine($"答:第10次落地时，共经过{sum}米，10次反弹{height}米");

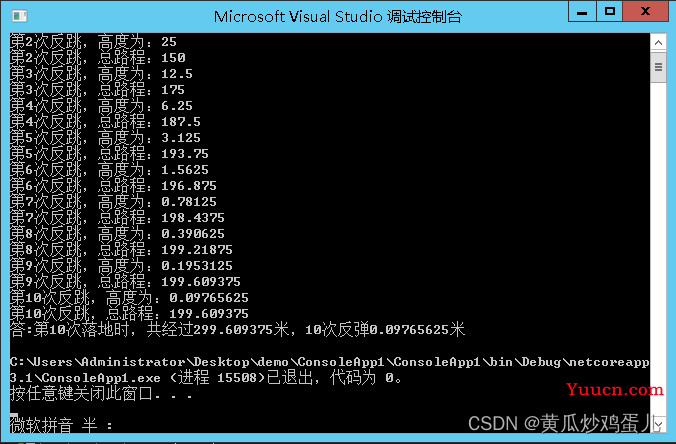
CSDN别的博主些的文章，保留了3位小数