本文展示的是使用 Pytorch 构建一个 BiLSTM 来实现情感分析。本文的架构是第一章详细介绍 BiLSTM，第二章粗略介绍 BiLSTM（就是说如果你想快速上手可以跳过第一章），第三章是核心代码部分。

1. BiLSTM的详细介绍

坦白的说，其实我也不懂 LSTM，但是我这里还是尽我最大的可能解释这个模型。这里我就盗个图 [1]（懒得自己画了，而且感觉好像他也是盗的李宏毅老师课件的图）。

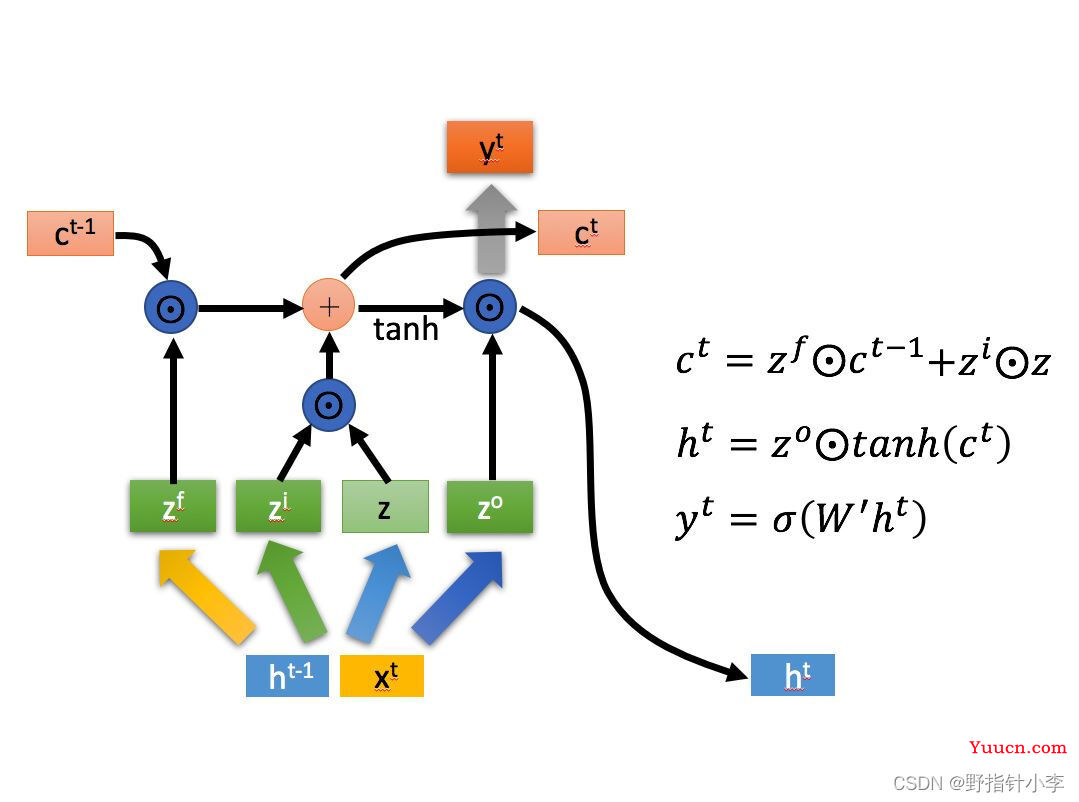
简单来说，LSTM 在每个时刻的输入都是由该时刻输入的序列信息
X
t
X^t
Xt 与上一时刻的隐藏状态
h
t
−
1
h^{t-1}
ht−1 通过四种不同的非线性变化映射而成，分别为：

1. 遗忘门控信号：遗忘门控信号
   z
   f
   z^f
   zf 的计算公式如下：
   
   z
   f
   =
   s
   i
   g
   m
   o
   i
   d
   (
   W
   f
   [
   X
   t
   ;
   h
   t
   −
   1
   ]
   )
   ,
   z^f = {\rm sigmoid}(W^f\left[ X^t; h^{t-1} \right]),
   zf=sigmoid(Wf[Xt;ht−1]),
   其中，
   [
   X
   t
   ;
   h
   t
   −
   1
   ]
   [X^t;h^{t-1}]
   [Xt;ht−1] 是将
   X
   t
   X^t
   Xt 与
   h
   t
   −
   1
   h^{t-1}
   ht−1 拼接起来；
   W
   f
   W^f
   Wf 是权重；$\mathrm{Sigmoid}(\cdot )$ 是 Sigmoid 激活函数，用于将数据映射到 (0, 1) 的区间范围内。
2. 记忆门控信号：记忆门控信号
   z
   i
   z^i
   zi 的计算公式如下：
   
   z
   i
   =
   s
   i
   g
   m
   o
   i
   d
   (
   W
   i
   [
   X
   t
   ;
   h
   t
   −
   1
   ]
   )
   .
   z^i={\rm sigmoid}(W^i\left[ X^t; h^{t-1} \right]).
   zi=sigmoid(Wi[Xt;ht−1]).
3. 输出门控信号：输出门控信号
   z
   o
   z^o
   zo 的计算公式如下：
   
   z
   o
   =
   s
   i
   g
   m
   o
   i
   d
   (
   W
   o
   [
   X
   t
   ;
   h
   t
   −
   1
   ]
   )
   .
   z^o = {\rm sigmoid}(W^o\left[ X^t; h^{t-1} \right]).
   zo=sigmoid(Wo[Xt;ht−1]).
4. 当前时刻的信息：当前时刻的信息 $z$ 的计算公式如下：
   
   z
   =
   t
   a
   n
   h
   (
   W
   [
   X
   t
   ;
   h
   t
   −
   1
   ]
   )
   ,
   z = {\rm tanh}(W\left[ X^t; h^{t-1} \right]),
   z=tanh(W[Xt;ht−1]),
   其中，$\tanh (\cdot )$ 是将数据放缩到 (-1, 1) 的区间内。

通过以上的公式，我们可以发现，
z
f
,
z
i
,
z
o
z^f, z^i, z^o
zf,zi,zo 都是 (0, 1) 区间的值，而 $z$ 是 (-1, 1) 区间的值。

接着就是 LSTM 的内部计算公式，即图上所示的那几个，分别为：

1. 当前时刻的细胞状态
   c
   t
   c^t
   ct 的计算公式如下：
   
   c
   t
   =
   z
   f
   ⊙
   c
   t
   −
   1
   +
   z
   i
   ⊙
   z
   ,
   c^t = z^f \odot c^{t-1} + z^i \odot z,
   ct=zf⊙ct−1+zi⊙z,
   其中，$\odot$ 是哈达玛积，即矩阵元素对位相乘，但是需要注意的是，哈达玛积数学上不可解释，但是跑出来效果好。
2. 当前时刻的隐藏状态
   h
   t
   h^t
   ht 的计算公式如下：
   
   h
   t
   =
   z
   o
   ⊙
   t
   a
   n
   h
   (
   c
   t
   )
   .
   h^t = z^o \odot {\rm tanh} (c^t).
   ht=zo⊙tanh(ct).
3. 当前时刻的输出
   y
   t
   y^t
   yt 的计算公式如下：
   
   y
   t
   =
   σ
   (
   W
   ′
   h
   t
   )
   .
   y^t = \sigma (W'h^t).
   yt=σ(W′ht).

公式列举完后，这里说一下我对这些公式的理解（不一定是对的哈）。

• 首先是
  c
  t
  c^t
  ct 的计算。我们看到
  c
  t
  c^t
  ct 的计算分为了两部分。一部分是
  z
  f
  ⊙
  c
  t
  −
  1
  z^f \odot c^{t-1}
  zf⊙ct−1，这一部分是 LSTM 的遗忘过程，由于刚刚提到，
  z
  f
  z^f
  zf 是 (0, 1) 区间范围内的值，同时，sigmoid 函数是一个无限趋近于 0 或者 1 的函数，也就是说，
  c
  t
  −
  1
  c^{t-1}
  ct−1 无论怎样，都会有些数据被遗弃，始终不会完全保留下来，这也就模拟了一个遗忘的过程。同理，对于记忆部分
  z
  i
  ⊙
  z
  z^i \odot z
  zi⊙z，这一步也是只会保留部分 $z$ 的信息，也就模拟了人的记忆是由些许失真的过程。同时，两者相加后，那么就代表了当前细胞状态
  c
  t
  c^t
  ct 中保留的是没有被遗忘掉的过去的信息和当前时刻被记忆下来的信息。
• 接着是
  h
  t
  h^t
  ht 的计算。首先是为什么要先对
  c
  t
  c^t
  ct 做一次 $\tanh (\cdot )$，这是因为由于
  c
  t
  c^t
  ct 的区间范围不是 (-1, 1)，因为
  z
  i
  ⊙
  z
  z^i \odot z
  zi⊙z 的区间范围是 (-1, 1)，再与
  z
  f
  ⊙
  c
  t
  −
  1
  z^f \odot c^{t-1}
  zf⊙ct−1 相加，那么
  c
  t
  c^t
  ct 的范围就有可能超出 (-1, 1)，所以先用一个 tanh 将数值给放缩到 (-1, 1) 内。接着再与
  z
  o
  z^o
  zo 做一次哈达玛积后，得到的隐藏状态就是 (-1, 1) 的数据，那么该数据放到后续模块中，就可以代表当前时刻的输入是正的还是负的，同时有多大。
• 最后就是
  y
  t
  y^t
  yt 的计算，实际上这就是个全连接层，将隐藏状态进行一次映射，再通过一个非线性变化的激活函数。

2. BiLSTM 的简单介绍

当然，其实你没看懂上面的部分也不重要，从使用的角度上来讲，会用就行了，就像你用手机，你不会去搞懂里面每个元器件是怎么做出来的，每个 APP 是怎么写出来的；就像你去打篮球，也不用梳个中分，穿个背带裤。

那么对于 BiLSTM，你需要了解的是什么？

• 首先，这是一个序列模型，它接受一个序列的输入，并且输出这个序列的信息。对于序列中每个位置的输出，它会包含该位置的信息以及之前的信息。就是说 LSTM 能够捕获到位置 $t$ 及其之前位置的信息。而对于 BiLSTM 的话，则能捕获到 $t$ 的双向信息。
• 如果是 BiLSTM，它的每个位置的输出，是前向
  L
  S
  T
  M
  →
  \overrightarrow{LSTM}
  LSTM 的输出
  y
  →
  \overrightarrow{y}
  y​ 与反向
  L
  S
  T
  M
  ←
  \overleftarrow{LSTM}
  LSTM 的输出
  y
  ←
  \overleftarrow{y}
  y​ 拼接在一起的，
  [
  y
  →
  ;
  y
  ←
  ]
  [\overrightarrow{y}; \overleftarrow{y}]
  [y​;y​]。所以假设你设置 LSTM 的隐藏层维度为 128，那么单向 LSTM 的输出维度是 128，但是双向就是 256 （128*2）.
• 但是虽然说 LSTM 好像大概可能也许 maybe possibly 能够捕获长距离依赖信息哈，毕竟 LSTM 的全称都是 Long Short-Term Memory，但是实际上这是 LSTM 的骗局，LSTM 并没有捕获长距离依赖信息的能力！LSTM 并没有捕获长距离依赖信息的能力！LSTM 并没有捕获长距离依赖信息的能力！ 从数学上说，你经过这么多次 sigmoid，还能保留个啥？当然，在《An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling》这篇论文[2]中，作者用了大量的实验来说明了，LSTM 不仅并行计算能力差（因为要上一个时间步的信息才能计算下一个时间步，所以 LSTM 不是个并行系统），同时在它最吹嘘的长距离信息捕获能力上，都不如 CNN，所以以后在跑实验的时候，可以尝试使用 TextCNN 来试试，说不定效果比 BiLSTM 好（反正我做过的实验中 TextCNN 性能一般比 BiLSTM 高8-10个点）。

3. BiLSTM 实现情感分析

• 全部代码在 github 上，网址为：https://github.com/Balding-Lee/Pytorch4NLP
• 我采用的是 IMDb 数据集，由于数据集没有验证集，而且读取起来很麻烦，所以我将数据给读取出来，放到了一个文件中，并且将训练集中的10%划分为了验证集，数据集链接如下： https://pan.baidu.com/s/128EYenTiEirEn0StR9slqw ，提取码：xtu3 。
• 采用的词嵌入是谷歌的词嵌入，词嵌入的链接如下：链接：https://pan.baidu.com/s/1SPf8hmJCHF-kdV6vWLEbrQ ，提取码：r5vx

在本博客中仅介绍模型部分，详细代码见 github。

模型图如图所示：

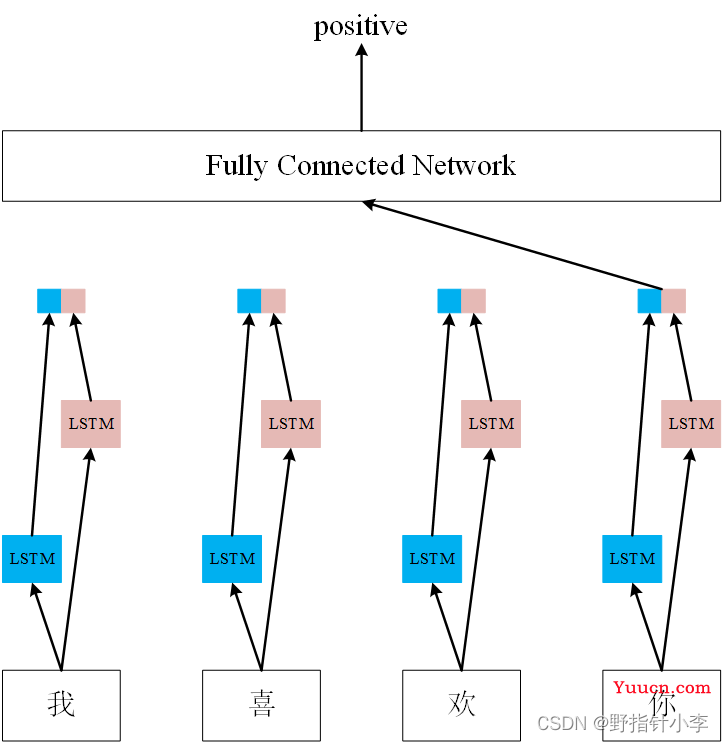
具体而言，就是输入序列输入到一个双向 LSTM 中，并将双向 LSTM 的最后一个隐藏状态（即句向量）输入到一个全连接层（也可以说是分类器）中，输出最后的分类结果，具体模型的代码如下：

import torch.nn as nn
class BiLSTM_SA(nn.Module):
    def __init__(self, embed, config):
        super().__init__()
        self.embedding = nn.Embedding.from_pretrained(embed, freeze=False)
        self.LSTM = nn.LSTM(config.embed_size, config.lstm_hidden_size,
                            num_layers=config.num_layers, batch_first=True,
                            bidirectional=True)
        # 因为是双向 LSTM, 所以要乘2
        self.ffn = nn.Linear(config.lstm_hidden_size * 2,
                             config.dense_hidden_size)
        self.relu = nn.ReLU()
        self.classifier = nn.Linear(config.dense_hidden_size,
                                    config.num_outputs)
    def forward(self, inputs):
        # shape: (batch_size, max_seq_length, embed_size)
        embed = self.embedding(inputs)
        # shape: (batch_size, max_seq_length, lstm_hidden_size * 2)
        lstm_hidden_states, _ = self.LSTM(embed)
        # LSTM 的最后一个时刻的隐藏状态, 即句向量
        # shape: (batch, lstm_hidden_size * 2)
        lstm_hidden_states = lstm_hidden_states[:, -1, :]
        # shape: (batch, dense_hidden_size)
        ffn_outputs = self.relu(self.ffn(lstm_hidden_states))
        # shape: (batch, num_outputs)
        logits = self.classifier(ffn_outputs)
        return logits

全连接层我采用了两个全连接层，一个将维度从 256 压缩到 128，另外一个是分类器。

这里有个小细节要注意一下，通常在论文的公式里面，我们都会看到别人写的分类器的公式如下：
y
^
=
S
o
f
t
m
a
x
(
W
h
+
b
)
\hat{y} = {\rm Softmax}(Wh+b)
y​=Softmax(Wh+b)，有个 softmax 的激活函数，但是在 pytorch 中实际不需要，就比如我代码里面是写的：

logits = self.classifier(ffn_outputs)

而不是：

y_hat = self.softmax(self.classifier(ffn_outputs))

这是因为如果你后面选用交叉熵作为损失函数，而且调用的是torch中的 nn.CrossEntropyLoss()，那么就没必要在输出的时候用 softmax，这是因为 nn.CrossEntropyLoss() 中自带有 softmax 操作，虽然这样对你的分类结果不会产生任何影响，但是你得损失会变得很大。

最后的测试集的实验结果为：

test loss 0.419664 | test accuracy 0.813760 | test precision 0.804267 | test recall 0.829360 | test F1 0.816621

参考

[1] 陈诚. 人人都能看懂的LSTM[EB/OL]. https://zhuanlan.zhihu.com/p/32085405, 2018
[2] Shaojie Bai, J. Zico Kolter, Vladlen Koltun. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling [EB/OL]. https://arxiv.org/abs/1803.01271, 2018