💭 写在前面：我们先介绍线性方程体系的基本概念和矩阵表示方法，矩阵的定义、加法、乘法、逆矩阵、转置和标量乘法等。然后讲解如何解决线性方程组问题，包括解集形式、行阶梯形矩阵、计算逆置和解决线性方程组的算法等。本节将补充线性代数的基础知识，为后续的机器学习打好基础。
📜 文章目录：
Ⅰ. 线性方程体系（Systems of Linear Equations）
0x00 介绍
0x01 矩阵表示（Matrix Representation）
Ⅱ. 矩阵（Matrices）
0x00 矩阵的定义（Matrix: Definition）
0x01 矩阵加法与乘法
0x02 身份矩阵和矩阵属性（Identity Matrix and Matrix Properties）
0x03 逆矩阵和转置（Inverse and Transpose）
0x04 标量乘法（Scalar Multiplication）
Ⅲ. 解线性方程组问题（Solving Systems of Linear Equations）
0x00 解集形式
0x01 General = Particular + Homogeneous
0x02 行阶梯形矩阵（Row-Echelon Form）
0x03 计算逆置（Calculating the Inverse）
0x04 解决线性方程组的算
Ⅰ. 线性方程体系（Systems of Linear Equations）
0x00 介绍
我们先看看什么是代数：代数即一组对象、一组操作这些对象的规则或操作。
线性代数 (Linear algebra)：对象：vectors 
操作符：它们的加法 
和标量乘法 
。
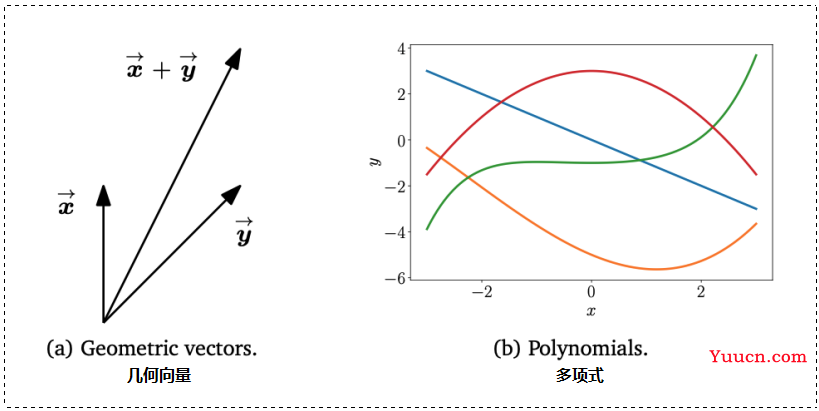
例子：几何矢量、多项式、音频信号、
元素。
对于未知变量 
：
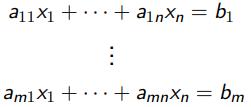
三种情况的解决方案：
无解 (No solution)：
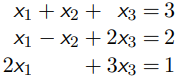
惟一解 (Unique solution) ：
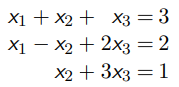
无穷多解 (Infinitely many solutions) ：
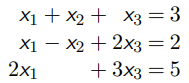
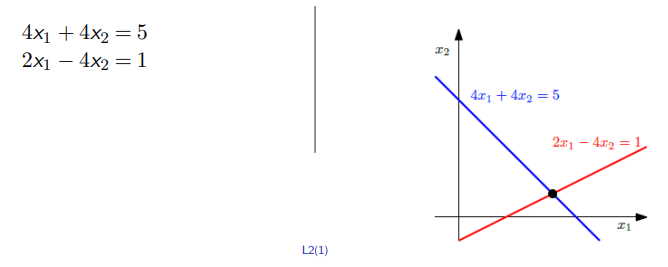
几何解释：
在一个有两个变量 
的线性方程组中，每个线性方程都在 
平面上定义了一条线。
由于线性方程组的解必须同时满足所有方程，所以解集是这些线的交点。
这个交集可以是一条线（若线性方程描述的是同一条线），一个点，或者是空的（当线是平行的）。
0x01 矩阵表示（Matrix Representation）
一个线性方程的集合
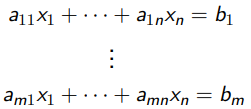
矩阵表示：
理解 
是回答关于这个线性系统 
的各种问题的关键。
Ⅱ. 矩阵（Matrices）
0x00 矩阵的定义（Matrix: Definition）
矩阵是一个按照矩形排列的数学对象，由一组数按照固定的行列顺序排列而成。
对于 
，
，实值 
矩阵 是元素 
的 
元组，
是根据由 行和 
列组成的矩形方案排序（通常用方括号或圆括号来表示）：
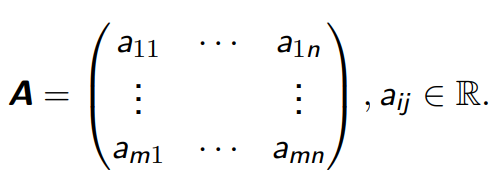
按照惯例，
矩阵称为行，
矩阵称列。这些特殊矩阵也称为 行 / 列向量。
矩阵实值的集合通常表示为 
，其中 和 分别表示矩阵的行数和列数，
表示实数集合。因此， 表示由 行 列实数元素构成的矩阵集合。
例如，下面是一个 2x3 的实数矩阵：
是所有 矩阵实值的集合，通过堆叠矩阵的所有 列转换为长矢量，
可等价表示为 
：
矩阵在数学中有着广泛的应用，例如线性代数、微积分、概率论等领域。其中，矩阵在线性代数中扮演着重要的角色，被用来表示线性变换和解决线性方程组等问题。
0x01 矩阵加法与乘法
加法：矩阵加法是指将两个相同维度的矩阵按照相同位置的元素相加得到一个新的矩阵。
需要注意的是，两个矩阵相加的前提是它们的维度相同，即行数和列数都相等。
对于两个矩阵 
：
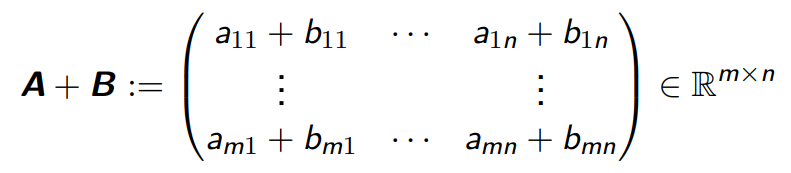
乘法：对于两个矩阵 
，其乘积 
的元素 
为：
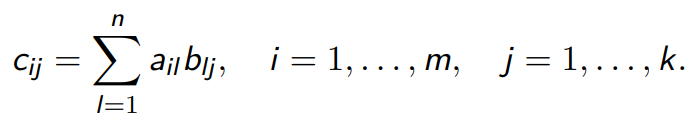
比如：（前行乘后列）
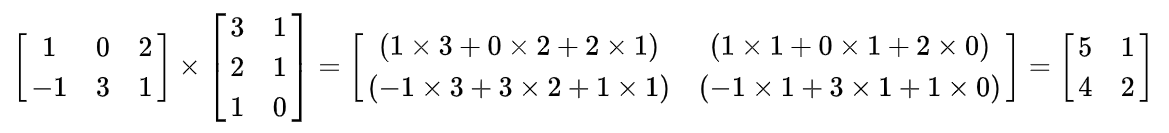
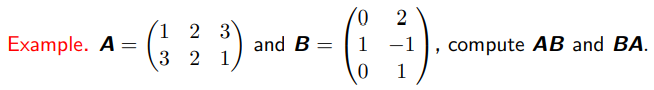
代码演示：矩阵的加法
import numpy as np
A = np.array([[1, 2, 3], [4, 5, 6]]) # 定义矩阵 A
B = np.array([[7, 8, 9], [10, 11, 12]]) # 定义矩阵 B
C = A + B
print("矩阵 A：")
print(A)
print("矩阵 B：")
print(B)
print("矩阵 C（A + B）：")
print(C)
🚩 运行结果如下：
矩阵 A：
[[1 2 3]
[4 5 6]]
矩阵 B：
[[ 7 8 9]
[10 11 12]]
矩阵 C（A + B）：
[[ 8 10 12]
[14 16 18]]
0x02 身份矩阵和矩阵属性（Identity Matrix and Matrix Properties）
身份矩阵：其对角线上的元素均为 1，其余元素均为 0 的矩阵，我们称之为身份矩阵 (Identity Matrix, IM)。身份矩阵是唯一的，也就是说，任何一个 n 阶方阵，如果其对角线上的元素均为 1，其余元素均为 0，那么它都是一个身份矩阵。
我们通常用 
表示身份矩阵，例如 3 x 3 的身份矩阵可以表示为：
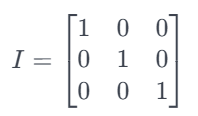
一个方阵 
，
， 其中 是行和列的数量。比如：
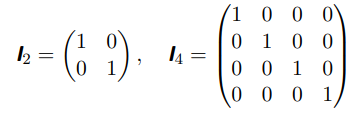
在 NumPy 中，我们可以使用 numpy.eye() 函数创建身份矩阵。
# 创建一个的身份矩阵的代码示例
import numpy as np
identity_matrix = np.eye(3)
print(identity_matrix)
🚩 运行结果如下：
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
0x03 逆矩阵和转置（Inverse and Transpose）
逆矩阵：逆矩阵是指一个方阵 的逆矩阵 
，满足以下条件：
-
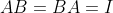，其中 是单位矩阵。 -
和 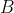都是可逆的矩阵。
如果矩阵 是可逆的，那么它的逆矩阵 可以通过下列公式计算：
其中，
是矩阵 的行列式，
是矩阵 的伴随矩阵。如果矩阵 不可逆，则其逆矩阵不存在。注意：逆矩阵只适用于方阵，而且只有当矩阵A可逆时才有逆矩阵存在。
对于一个方形矩阵 
， 是 的逆，用 
表示，如果：
如果存在，被称为 正则 (regular)、可逆 (invertible)、非正则 (nonsingular)。
如果存在，那就是唯一的 (unique)。
如何计算？对于 2×2 矩阵：
转置 (Transpose)：将矩阵的行和列互换得到的新矩阵。
对于一个矩阵 ，
，
是 的转置，我们用 
表示：
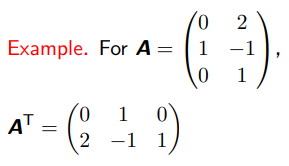
再比如，对于一个 3 行 2 列的矩阵 ：
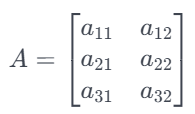
其转置矩阵 为一个 2 行 3 列的矩阵，每个元素的位置与原矩阵相反，如下所示：
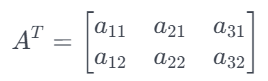
若 
，则称 为对称的 (symmetric) 。
矩阵的转置满足以下几个性质：
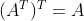，即对矩阵进行两次转置得到的仍是原矩阵。
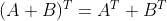，即对两个矩阵的和进行转置等于这两个矩阵的转置分别相加。
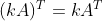，即对一个矩阵的所有元素乘以一个常数 
并进行转置等于先进行转置再将每个元素乘以 。
更多性质：
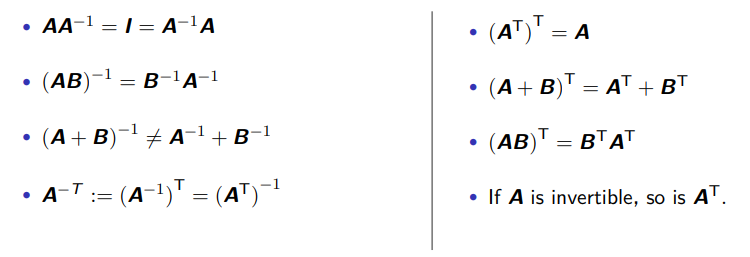
我们可以使用 numpy.linalg.inv() 函数来计算矩阵的逆矩阵：
import numpy as np
A = np.array([[1, 2], [3, 4]])
A_inv = np.linalg.inv(A)
print(A_inv)
用 numpy.transpose() 函数来计算矩阵的转置：
import numpy as np
A = np.array([[1, 2, 3], [4, 5, 6]])
A_transpose = np.transpose(A)
print(A_transpose)🚩 运行结果如下：
array([[1, 4],
[2, 5],
[3, 6]])
0x04 标量乘法（Scalar Multiplication）
用标量 
乘以 
，比如：
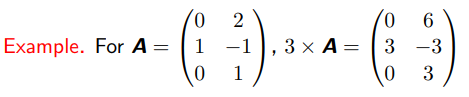
结合性 (Associativity) ：
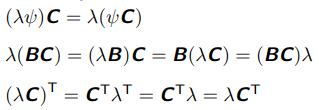
分配性 (Distributivity)：
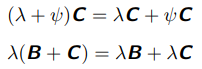
Ⅲ. 解线性方程组问题（Solving Systems of Linear Equations）
两个非零行给出 
和 
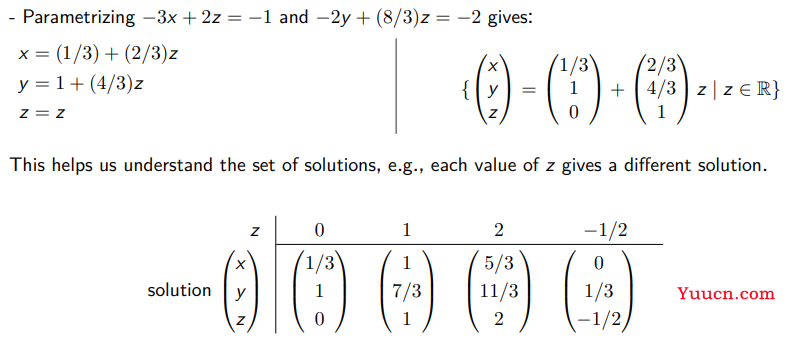
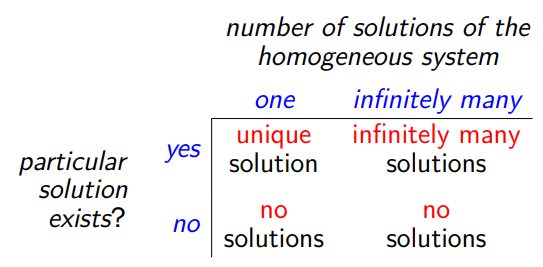
0x00 解集形式
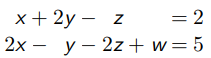以此方式还原：
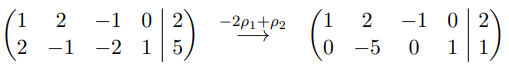
它有这种形式的解决方案：
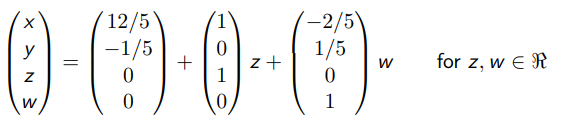
请注意，取 
表明第一个向量是系统的一个特定解 (particular solution) 。
0x01 General = Particular + Homogeneous
一般方法：
- 1. 寻找
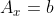的特定解 - 2. 寻找同质方程
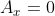的所有解，0 是一个平凡解(trivial solution) 。 - 3. 将步骤 1. 和 2. 的解合并为一般解 (general solution)。
问题：一个正式的算法可以执行上述内容？
- Gauss-Jordan 方法：转换为 "优美" 的形式（形式上减少了 row-echelon 形式）。
- 基本转换：（i）行交换（ii）乘以一个常数（iii）行加法
这样的形式允许用一种算法来解决线性方程的问题。
0x02 行阶梯形矩阵（Row-Echelon Form）
行阶梯形矩阵是指一个矩阵的行具有以下特点：
- 所有的零行都在矩阵的底部；
- 非零行的首个非零元素（称为主元）在上一行主元的右侧；
- 每一行的主元都在该行的所有其它元素的左侧。
比如：
其中，第一行的主元是1，第二行的主元是1，第三行的主元是1，第四行的主元是1。该矩阵的前四行是行阶梯形矩阵，而最后一行是一个零行。
定义：在下列情况下，一个矩阵是 row-echelon （行阶梯形矩阵）形式。
所有只包含零的行都在矩阵的底部；相应地，所有包含至少一个非零元素的行都在只包含零的行的上面。只看非零行，从左边开始的第一个非零数（也叫支点或前导系数）总是严格地在它上面一行的支点的右边。在 row-echelon 中与枢轴相对应的变量被称为基本变量，其他变量为自由变量。
在下列情况下，方程组为 reduced row-echelon 形式：。
- 它是 row-echelon 形式的。
- 每个支点都是 1。
- 枢轴是其列中唯一的非零条目。
高斯消除法 是一种进行基本转换的算法，它可以将线性方程组带入 row-echelon 形式。
Example: Unique Solution：
Example: Infinite Number of Solutions
0x03 计算逆置（Calculating the Inverse）
为了计算 的逆 ，我们需要找到一个矩阵 
，满足 
。那么，
。
我们可以把它写成一组同时进行的线性方程 ，其中我们求解 
。
我们用增强的矩阵符号来表示这组线性方程组，得到 
。
这意味着，如果我们将增强的方程组带入简化的 row-echelon 形式，我们可以在方程组的右侧读出逆数。
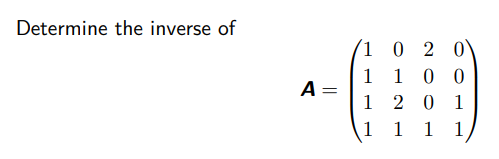
解决方案集的案例：
0x04 解决线性方程组的算法
伪逆 (Pseudo-inverse)
-
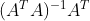：摩尔-彭若斯伪逆 (Moore-Penrose pseudo-inverse) - 许多计算：矩阵乘法、逆法等
高斯消除法 (Gaussian elimination)
- 直观和建设性的方式
- 立体复杂度（就同时方程数而言）
迭代法 (Iterative methods)
间接求解的实用方法：
- 固定的迭代方法：Richardson方法、Jacobi方法、Gaus-Seidel方法、逐次过度放松方法
- Krylov 子空间方法：共轭梯度、广义最小残差、双共轭梯度。
📌 [ 笔者 ] 王亦优
📃 [ 更新 ] 2023.3.15
❌ [ 勘误 ] /* 暂无 */
📜 [ 声明 ] 由于作者水平有限，本文有错误和不准确之处在所难免，
本人也很想知道这些错误，恳望读者批评指正！|
📜 参考资料 Marc Peter Deisenroth, A. Aldo Faisal, and Cheng Soon Ong. Mathematics for machine learning. Cambridge University Press, 2020 Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. . 百度百科[EB/OL]. []. https://baike.baidu.com/. |