激活函数（Relu，sigmoid，Tanh，softmax）详解

目录

1 激活函数的定义

2 激活函数在深度学习中的作用

3 选取合适的激活函数对于神经网络有什么样的重要意义

4 常用激活函数

4.1 Relu 激活函数

4.2 sigmoid 激活函数

4.3 Tanh激活函数

4.4 softmax 激活函数

---

1 激活函数的定义

激活函数（Activation Function），就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。

激活函数（Activation functions）对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。

2 激活函数在深度学习中的作用

如果不用激励函数（其实相当于激励函数是f(x) = x），在这种情况下你每一层节点的输入都是上层输出的线性函数，很容易验证，无论你神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，这种情况就是最原始的感知机（Perceptron）了，那么网络的逼近能力就相当有限。正因为上面的原因，我们决定引入非线性函数作为激励函数，这样深层神经网络表达能力就更加强大（不再是输入的线性组合，而是几乎可以逼近任意函数）。

激活函数有非线性，可微性，单调性，输出值的范围等性质。

3 选取合适的激活函数对于神经网络有什么样的重要意义

 层数比较多的神经网络模型在训练的时候会出现梯度消失(gradient vanishing problem)和梯度爆炸(gradient exploding problem)问题。梯度消失问题和梯度爆炸问题一般会随着网络层数的增加变得越来越明显。梯度消失会使网络训练不动，甚至使模型的学习停滞不前。梯度爆炸一般出现在深层网络和权值初始化值太大的情况下，梯度爆炸会引起网络不稳定，最好的结果是无法从训练数据中学习，而最坏的结果是出现无法再更新的NaN权重值。

        例如，一个网络含有三个隐藏层，梯度消失问题发生时，靠近输出层的hidden layer 3的权值更新相对正常，但是靠近输入层的hidden layer1的权值更新会变得很慢，导致靠近输入层的隐藏层权值几乎不变，仍接近于初始化的权值。这就导致hidden layer 1 相当于只是一个映射层，对所有的输入做了一个函数映射，这时此深度神经网络的学习就等价于只有后几层的隐藏层网络在学习。梯度爆炸的情况是：当初始的权值过大，靠近输入层的hidden layer 1的权值变化比靠近输出层的hidden layer 3的权值变化更快，就会引起梯度爆炸的问题。

        梯度消失和梯度爆炸问题都是因为网络太深，网络权值更新不稳定造成的，本质上是因为梯度反向传播中的连乘效应。对于更普遍的梯度消失问题，可以考虑一下三种方案解决：

1.    用ReLU等替代sigmoid函数。

2.    用Batch Normalization。

3.    LSTM的结构设计也可以改善RNN中的梯度消失问题。

4 常用激活函数

早期研究神经网络主要采用sigmoid函数或者tanh函数，输出有界，很容易充当下一层的输入。
近些年Relu函数及其改进型（如Leaky-ReLU、P-ReLU、R-ReLU等）在多层神经网络中应用比较多。下面我们来总结下这些激活函数：

4.1 Relu 激活函数

Relu函数表达式：

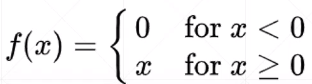
函数，及其导数图像：

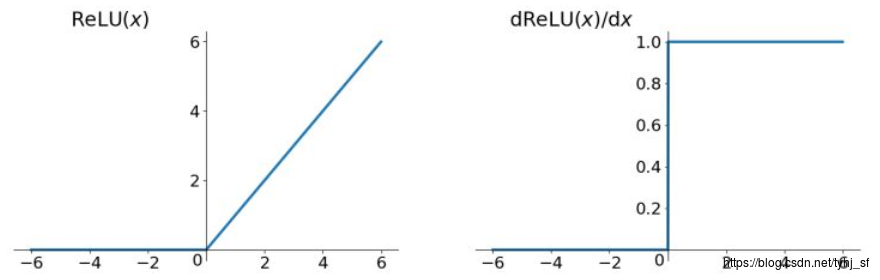
自定义代码：

函数表达式：f(x) = 1/(1+e^-x)
函数特点：
优点：1.输出[0,1]之间；2.连续函数，方便求导。
缺点：1.容易产生梯度消失；2.输出不是以零为中心；3.大量运算时相当耗时（由于是幂函数）。
函数定义：
def sigmoid(x):
    y = 1/(1+np.exp(-x))
    return y

pytorch代码：

# ReLU函数在torch中如何实现
import torch
a = torch.linspace(-1,1,10)
b = torch.relu(a)
print(a)
print(b)

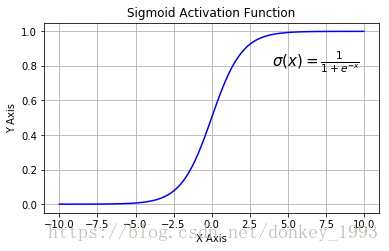
4.2 sigmoid 激活函数

函数表达式：

函数图像：

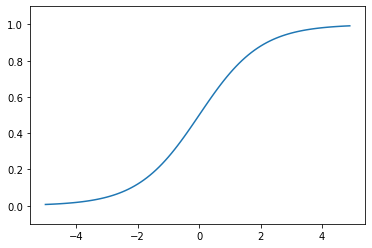
 函数导数图像：

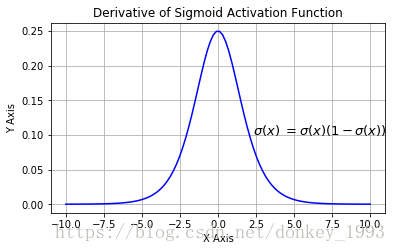
自定义代码：

函数表达式：f(x) = 1/(1+e^-x)
函数特点：
优点：1.输出[0,1]之间；2.连续函数，方便求导。
缺点：1.容易产生梯度消失；2.输出不是以零为中心；3.大量运算时相当耗时（由于是幂函数）。
函数定义：
def sigmoid(x):
    y = 1/(1+np.exp(-x))
    return y

pytorch代码：

# sigmoid函数在torch中如何实现
import torch
# a从-100到100中任取10个数
a = torch.linspace(-100,100,10)
print(a)
# 或者F.sigmoid也可以 F是从from torch.nn import functional as F
b = torch.sigmoid(a)
print(b)

4.3 Tanh激活函数

函数表达式：

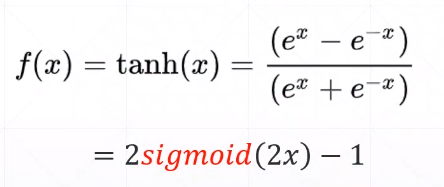
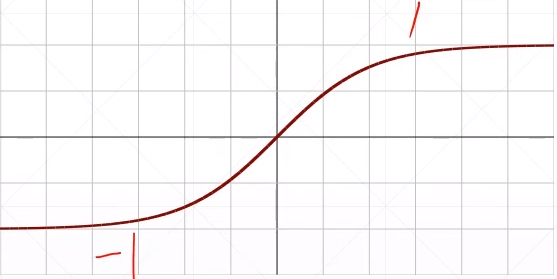
函数图像：

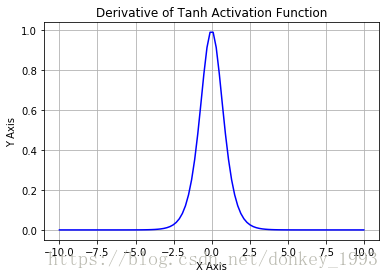
函数导数图像：

 自定义代码：

函数表达式：f(x) = (e^x-e^-x)/(e^x+e-x)
函数特点：
优点：1.输出[-1,1]之间；2.连续函数，方便求导；3.输出以零为中心。
缺点：1.容易产生梯度消失； 2.大量数据运算时相当耗时（由于是幂函数）。
函数定义：
def tanh(x):
    y = (np.exp(x) - np.exp(-x))/(np.exp(x) + np.exp(-x))
    return y

pytorch代码：

# tanh函数在torch中如何实现
import torch
a = torch.linspace(-10,10,10)
b = torch.tanh(a)
print(a)
print(b)

4.4 softmax 激活函数

函数表达式：

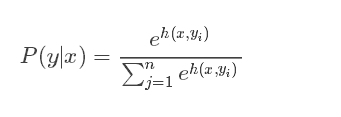
函数图像：

 函数导数图像：

自定义代码：

def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T
    x = x - np.max(x) # 溢出操作
    return np.exp(x) / np.sum(np.exp(x))