经实验证明,采用混沌映射产生随机数的适应度函数值有明显提高,用混沌映射取代常规的均匀分布的随机数发生器可以得到更好的结果,特别是搜索空间中有许多局部解时,更容易搜索到全局最优解,利用混沌序列进行种群初始化、选择、交叉和变异等操作会影响算法的整个过程,而且常常能取得比伪随机数更好的效果。
混沌主要具有以下两个性质:
- 轨道不稳定性,这个性质在适当的约束条件下导致运动的不稳定性和分叉现象
- 高度依赖初始值,即两个相近的初始值会得到完全不相同的随机数序列
描述混沌运动的一个典型例子,就是非线性Logistic映射,它是一个一维的非线性函数:
![]()
式中,μ为控制参数,且μ>1;xn的取值范围为0≤xn≤1。
本篇博客以logistic混沌映射为例来学习混沌映射的性质。
本文考虑控制参数μ在1<μ≤4范围内取值时,式(1)的映射情况。
-
当μ=2.8,x0=0.63时,经过20次迭代后的解为x20=0.642 7和x21=0.643 0,逐渐趋向于0.642 7和0.643 0之间的一个不动点。
-
当μ=3.14,x0=0.66时,经过30次迭代后的解稳定在两个不动点x30=0.538 1和x31=0.780 4附近。
-
当μ=3.45,x0=0.68时,经过68次迭代后的解稳定在4个不动点x68=0.429 4、x69=0.845 3、x70=0.451 1和x71=0.854 2附近。
-
当μ=4.0,x0=0.80时,迭代计算的结果不再出现趋于一个或几个不动点的情况,而是完全进入混沌状态,在这种情况下的取值是随机的。
这里需要说明的是,初始值x0均可以从0开始,这里的初值仅仅是为了读者验证的方便。
由以上4点分析可知,Logistic映射描述的非线性动力学中的混沌运动在某些条件下表现出高度的有序,如当μ=2.8时,迭代20次以后的解趋向于一个不动点,不再变化,这是有规律有序的运动。再加大μ值,这种有序的运动中出现稳定的不动点数将不断地增加。数量的增加仍然可以视为有序的,这种不动点数不断增加的情况称之为 “分叉现象” 。随着分叉不动点数的不断增加,使有序的运动逐渐失去平衡,进入混沌状态,即μ≥4.0的情况。因此,用μ=4.0代入式(1)就可以得到一组随机数: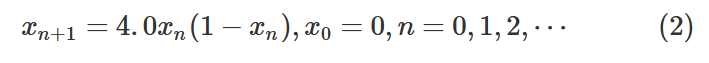
n值越大,得到的xn+1值就越大。通过给定不同初始值得到的相应随机数可以得知这些随机数具有高度依赖初始值的特点,即两个相近的初始值会得到完全不相同的随机数序列,这是混沌映射的性质,也是引用它的理论依据。这种性质将给优化计算带来很大的好处。
下面给出部分常用于群体智能领域的混沌序列:

参考资料:
混沌映射在优化计算中的应用
几种混沌映射