一、神经网络模型
神经网络(Neural Networks)是从微观结构与功能上对人脑神经系统进行模拟而建立起来的数学模型,它具有模拟人脑思维的能力,其特点主要是具有非线性特性、学习能力和自适应性等,是模拟人类智能的一种重要方法。神经网络是由神经元互联而成的,能接收并处理信息,而这种信息处理主要是由神经元之间的相互作用,即通过神经元之间的连接权值来处理并实现的。神经网络在人工智能、自动控制、计算机科学、信息处理和模式识别等领域得到了非常成功地应用。
根据生物神经元的结构与基本功能,可以将其简化为下图的形式,并建立神经网络模型的基础——人工神经元数学模型:
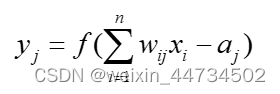
其中,![]() 表示神经元j的输出;
表示神经元j的输出;![]() 表示神经元i的输入;
表示神经元i的输入;![]() 表示神经元与神经元之间的连接权值;
表示神经元与神经元之间的连接权值;![]() 表示神经元的阈值;
表示神经元的阈值;![]() 是输入到输出传递函数(也称激活函数)。
是输入到输出传递函数(也称激活函数)。
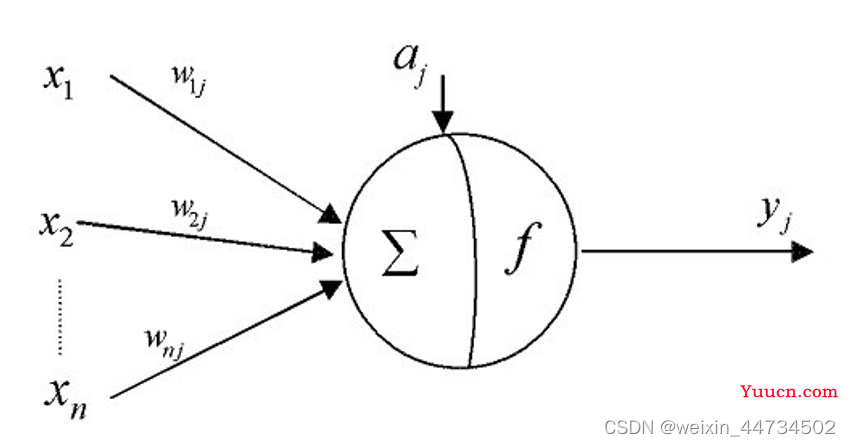
sigmod是常见的激活函数,后面的实例会经常用到。
二、神经网络模型BP算法
2.1 网络结构及工作方式
除单元特性外,网络的拓扑结构也是NN的一个重要特性。从连接方式看NN主要有两种。
(i)前馈型网络
各神经元接受前一层的输入,并输出给下一层,没有反馈。结点分为两类,即输入单元和计算单元,每一计算单元可有任意个输入,但只有一个输出(它可耦合到任意多个其它结点作为其输入)。通常前馈网络可分为不同的层,第i 层的输入只与第i −1层 输出相连,输入和输出结点与外界相连,而其它中间层则称为隐层。
(ii)反馈型网络
所有结点都是计算单元,同时也可接受输入,并向外界输出。 NN 的工作过程主要分为两个阶段:第一个阶段是学习期,此时各计算单元状态不变,各连线上的权值可通过学习来修改;第二阶段是工作期,此时各连接权固定,计算单元状态变化,以达到某种稳定状态。
从作用效果看,前馈网络主要是函数映射,可用于模式识别和函数逼近。反馈网络按对能量函数的极小点的利用来分类有两种:第一类是能量函数的所有极小点都起作 用,这一类主要用作各种联想存储器;第二类只利用全局极小点,它主要用于求解最优化问题。
(iii)向后传播算法(Back-Propagation)
对于反馈型网络所说的各连线上权值的修改,主要运用了向后传播算法(Back-Propagation),这也是三层BP神经网络模型的核心部分。
我们希望对应学习样本的输出非常精确,但实际上是不可能的只能希望实际输出尽可能地接近理想输出。为清楚起见,把对应于样品s的理想输出记为 ![]() ,那么
,那么
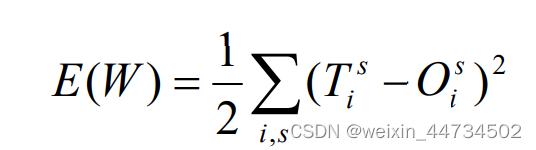
度量了在一组给定的权下,实际输出与理想输出的差异,由此,寻找一组恰当的权的问题,自然地归结为求适当W 的值,使 E(W ) 达到极小的问题。
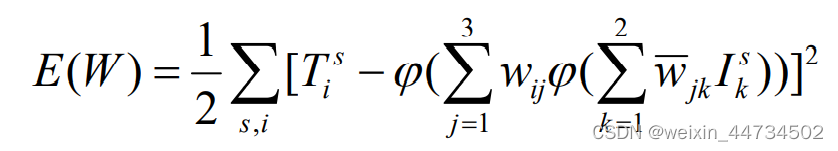
易知,对每一个变量![]() 或
或 ![]() 而言,这是一个连续可微的非线性函数,为了求得其极小点与极小值,最为方便的就是使用最速下降法。最速下降法是一种迭代算法,为求出 E(W ) 的(局部)极小,它从一个任取的初始点
而言,这是一个连续可微的非线性函数,为了求得其极小点与极小值,最为方便的就是使用最速下降法。最速下降法是一种迭代算法,为求出 E(W ) 的(局部)极小,它从一个任取的初始点![]() 出发,计算在
出发,计算在![]() 点的负梯度方向 -∇E (
点的负梯度方向 -∇E (![]() ) ,这是函数在该点下降最快的方向;只要∇E(
) ,这是函数在该点下降最快的方向;只要∇E(![]() ) ≠ 0 ,就可沿该方向移动 一小段距离,达到一个新的点 W1 = W0 −η∇E (
) ≠ 0 ,就可沿该方向移动 一小段距离,达到一个新的点 W1 = W0 −η∇E (![]() ) ,η 是一个参数,只要η 足够小, 定能保证 E( W1) < E (
) ,η 是一个参数,只要η 足够小, 定能保证 E( W1) < E (![]() ) 。不断重复这一过程,一定能达到 E 的一个(局部)极小点。 就本质而言,这就是 BP 算法的全部内容
) 。不断重复这一过程,一定能达到 E 的一个(局部)极小点。 就本质而言,这就是 BP 算法的全部内容
2.2 BP神经网络的拓扑结构如图所示。

其中,![]() 是神经网络的(实际)输入,
是神经网络的(实际)输入,![]() 是隐含层的输出,即为输出层的输入,
是隐含层的输出,即为输出层的输入,![]() 网络的(实际)输出,a,b分别为隐含层和输出层神经元(节点)的阈值,
网络的(实际)输出,a,b分别为隐含层和输出层神经元(节点)的阈值,![]() 分别为输入层到隐含层和隐含层到输出层的权值。也就是说,图中所表示的BP神经网络,它的输入层神经元(节点)个数为n,隐含层神经元(节点)个数为m,输出层神经元( 节点)个数为l,这种结构称为n-m-l结构的三层BP神经网络。
分别为输入层到隐含层和隐含层到输出层的权值。也就是说,图中所表示的BP神经网络,它的输入层神经元(节点)个数为n,隐含层神经元(节点)个数为m,输出层神经元( 节点)个数为l,这种结构称为n-m-l结构的三层BP神经网络。
2.3 BP神经网络学习算法及流程(以三层BP神经网络为例)


三、BP神经网络算法常用工具箱函数
3.1 newff——BP神经网络参数设置函数
函数功能:构建一个BP神经网络。
函数形式:net=newff(PR,[S1,S2,…,SN],{TF1,TF2,…,TFN},BTF,BLF,PF)
其中,PR:为样本数据组成的矩阵,由其中最大值和最小值组成的R×2维的矩阵;
Si:第i层的节点数,共计N层;
TFi:第i层节点的传递函数,包括线性传递函数purelin;正切S型传递函数tansig;对数S型传递函数logsig。默认为“tansig”;
BTF:训练函数,用于网络权值和阈值的调整,默认基于Levenberg_Marquardt共轭梯度法的训练函数trainlm。其它参数见后面表格。
BLF:网络的学习函数,包含BP学习规则learngd;带动量项的BP学习规则learngdm。默认为“learngdm”;
PF:网络的性能分析函数,包括均值绝对误差性能分析函数mae;均方性能分析函数mse。默认为“mse”。
一般在使用过程中设置前面4个参数,后面2个参数采用系统默认参数。
示例:net=newff([-1,1],[5,1],{'tansig','purelin'});
其中[-1,1]表示输入向量的最小最大值,也可用minmax(p);[5,1]表示隐藏层为5节,输出层为1节;tansig,purelin分布表示隐藏层和输出层的传递函数;
3.2 train——BP神经网络训练函数
函数功能:用训练函数训练BP神经网络。
函数形式:[net,tr]=train(NET,P,T)
NET:待训练网络,即newff所创建的初始网络;
P:输入数据矩阵;
T:期望输出数据矩阵;
net:训练好的网络;
tr:训练过程记录。
示例:

3.3 sim——BP神经网络预测/仿真函数
函数功能:用训练好的BP神经网络预测/仿真函数输出。
函数形式:Y=sim(net,x)
net:训练好的BP神经网络;
x:输入数据;
Y:网络预测/仿真数据,即网络实际输出。
示例
net=train(net,P,T); %网络训练函数,train中的net为创建的初始网络
Y=sim(net,P);%P为输入向量,Y为仿真结果
plot(P,T,'-',P,Y,'o');%T为原输出,将原来结果和仿真结果画在一个图中。
四、预测
4.1 分类问题
例1 生物学家试图对两种蠓虫(Af与Apf)进行鉴别,依据的资料是触角和翅膀的长度,已经测得了9支Af 和6支 Apf 的数据如下:Af: (1.24,1.27),(1.36,1.74),(1.38,1.64),(1.38,1.82),(1.38,1.90),(1.40,1.70), (1.48,1.82),(1.54,1.82),(1.56,2.08). Apf: (1.14,1.82),(1.18,1.96),(1.20,1.86),(1.26,2.00),(1.28,2.00),(1.30,1.96).
现在的问题是:
(i)根据如上资料,如何制定一种方法,正确地区分两类蠓虫。
(ii)对触角和翼长分别为(1.24,1.80),(1.28,1.84)与(1.40,2.04)的3个标本,用所得到的方法加以识别。
如上的问题是有代表性的,它的特点是要求依据已知资料(9支Af 的数据和6支-353- Apf 的数据)制定一种分类方法,类别是已经给定的(Af 或 Apf)。今后,我们将9支Af 及6支Apf 的数据集合称之为学习样本。
Matlab实现(这里每一步小编都给了详细注释,不再做其他说明)
clear
p1=[1.24,1.27;1.36,1.74;1.38,1.64;1.38,1.82;1.38,1.90;
1.40,1.70;1.48,1.82;1.54,1.82;1.56,2.08]; %9支Af的触角和翅膀的长度存在p1中
p2=[1.14,1.82;1.18,1.96;1.20,1.86;1.26,2.00
1.28,2.00;1.30,1.96]; %6支APf的触角和翅膀的长度存在p2中
p=[p1;p2]'; %将p1和p2合成一个矩阵并取转置,得到2行15列的矩阵p,第一列表示触角,第二列表示翅膀
pr=minmax(p); %求出P两列的最小值和最大值存在pr中
goal=[ones(1,9),zeros(1,6);zeros(1,9),ones(1,6)]; %写出已经15支的输出矩阵,Af为(1.0),Apf为(0,1)
plot(p1(:,1),p1(:,2),'h',p2(:,1),p2(:,2),'o') %把Af的触角~翅膀,及Apf触角~翅膀散点图画在同一个图中
net=newff(pr,[3,2],{'logsig','logsig'}); %用newff函数创建一个神经网络,隐藏层为3节,输出层为2节,隐藏层和输出层的传递函数均为logsig
net.trainParam.show = 10; %两次显示直接的训练字数(没有时取NAN)
net.trainParam.lr = 0.05; %学习速率为0.05
net.trainParam.goal = 1e-10; %训练目标
net.trainParam.epochs = 50000; %最大训练次数
net = train(net,p,goal); %从输入p到输出goal用已创建的net训练
x=[1.24 1.80;1.28 1.84;1.40 2.04]'; %输入想要预测的三支的触角和翅膀数据
y0=sim(net,p) %已知P的仿真,这里p即作为训练数据又作为仿真数据
y=sim(net,x)%对未知类型的x中三支进行仿真预测Af的触角~翅膀,及Apf触角~翅膀散点图画在同一个图1中,
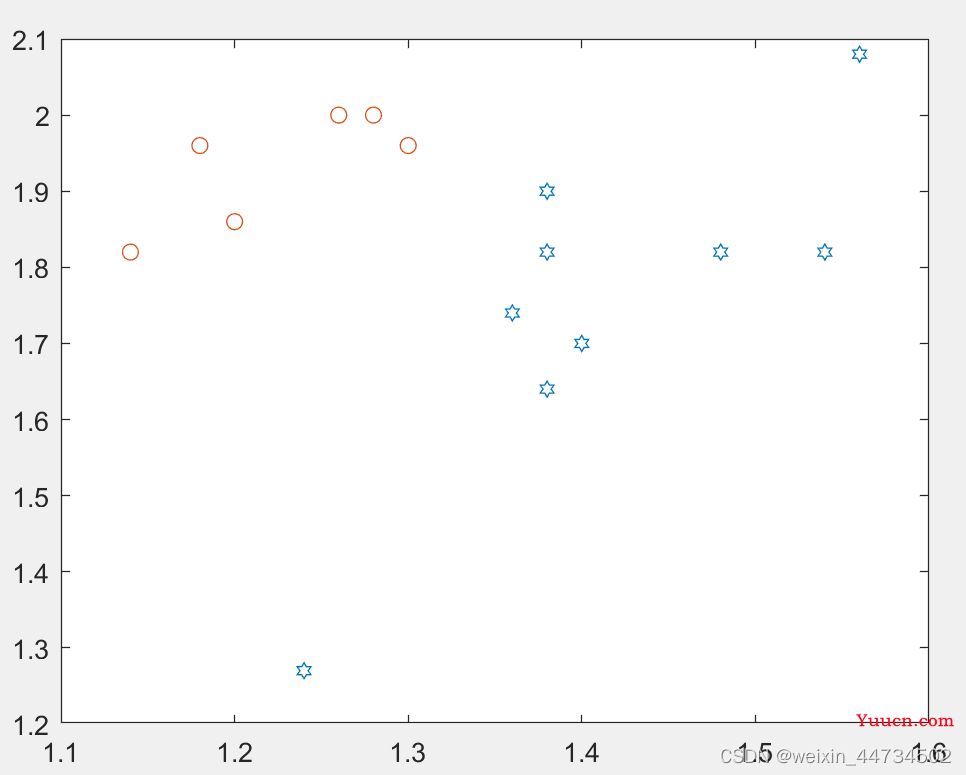
图1
其实,我们可以很容易发现,两类螨虫的触角~翅膀数据确实分布不同,当然这只是一种直观的判断,我们这里要用已经训练好的网络进行仿真,在训练到第14次时,已经达到最佳训练性能(如图2)。
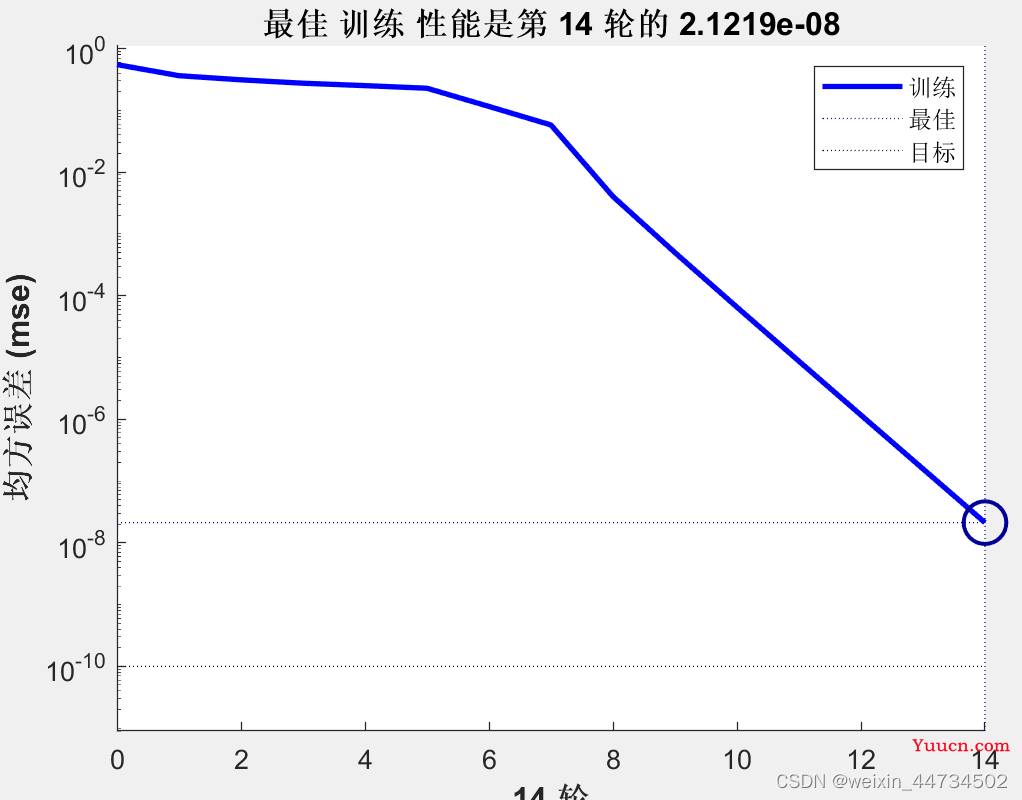
图2
利用训练好的网络对已知的15支螨虫数据进行仿真得到结果如表1
| 1 | 2 | 3 | 5 | 5 | 6 | 7 | 8 | 9 |
| 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9994 | 0.9999 | 1.0000 | 1.0000 | 1.0000 |
| 0.0001 | 0.0001 | 0.0000 | 0.0000 | 0.0001 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 10 | 11 | 12 | 13 | 14 | 15 |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0001 | 0.0005 |
| 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9999 | 0.9994 |
表1
我们可以发现,虽然仿真得到的结果和目标结果还不是百分百相同,但是肯定达到的分类的标准。
利用训练好的网络对(1.24,1.80),(1.28,1.84)与(1.40,2.04)的3个标本进行分类,得到结果如下表2
| 1 | 2 | 3 |
| 0.0001 | 0.0008 | 0.9503 |
| 0.9996 | 0.9974 | 0.0294 |
表2
所以(1.24,1.80),(1.28,1.84)属于Apf,(1.40,2.04)属于Af.
4.2 非线性映射问题
BP神经网络的一个重要功能就是非线性映射,这一功能非常适合于函数逼近等,简单来讲就是找出两组数据之间的关系
例2 已知输入向量P和目标向量T,建立一个BP网络,找出P和T之间的关系.已知P= -1:0.1:1;
T=[-0.96 -0.577 -0.0729 0.377 0.641 0.66 0.461 0.1336 -0.201 -0.434 -0.5 -0.393 -0.1647 0.0988 0.3072 0.396 0.3449 0.1816 -0.0312 -0.2183 -0.3201];
解:输入向量P、目标向量T分别为:
>>P= -1:0.1:1;
>>T=[-0.96 -0.577 -0.0729 0.377 0.641 0.66 0.461 0.1336 -0.201 -0.434 -0.5 -0.393 -0.1647 0.0988 0.3072 0.396 0.3449 0.1816 -0.0312 -0.2183 -0.3201];
首先,利用newff创建一个BP神经网络,代码为:
>>net=newff([-1,1],[5,1],{'tansig','purelin'});
其中,[-1,1]表示输入向量P的最小值和最大值,可以用minmax(P)代替。[5,1]表示网络的隐含层有5个神经元,输出层有1个神经元,也就是说,该BP神经网络为1-5-1结构的神经网络。{'tansig','purelin'}表示网络隐含层的传递函数为tansig,输出层的传递函数为purelin。由于没有特别设定训练函数,因此训练函数取默认值trainlm。
其次,设置训练参数并对网络进行训练。代码为:
>>net.trainParam.epochs=200; %最大训练次数
>>net.trainParam.goal=0; %训练目标
>>net.trainParam.show=50; %两次显示之间的训练次数
>>net=train(net,P,T); %网络训练函数,train中的net为创建的初始网络
最后,对训练好的训练进行仿真,得到网络输出结果Y,并作图。代码为:
>> Y=sim(net,P);
Matlan实现如下
P= -1:0.1:1;
T=[-0.96 -0.577 -0.0729 0.377 0.641 0.66 0.461 0.1336 -0.201 -0.434 -0.5 -0.393 -0.1647 0.0988 0.3072 0.396 0.3449 0.1816 -0.0312 -0.2183 -0.3201];
net=newff([-1,1],[5,1],{'tansig','purelin'});
net.trainParam.epochs=200; %最大训练次数
net.trainParam.goal=0; %训练目标
net.trainParam.show=50; %两次显示之间的训练次数
net=train(net,P,T); %网络训练函数,train中的net为创建的初始网络
Y=sim(net,P)%用训练好的网络对P仿真
plot(P,T,'-',P,Y,'o')%把训练样本和仿真画在一个图中最佳训练性能是第 61 轮的 2.7485e-06误差曲线如图3所示。为更直观地理解网络输出与目标向量之间的关系,见图4所示。
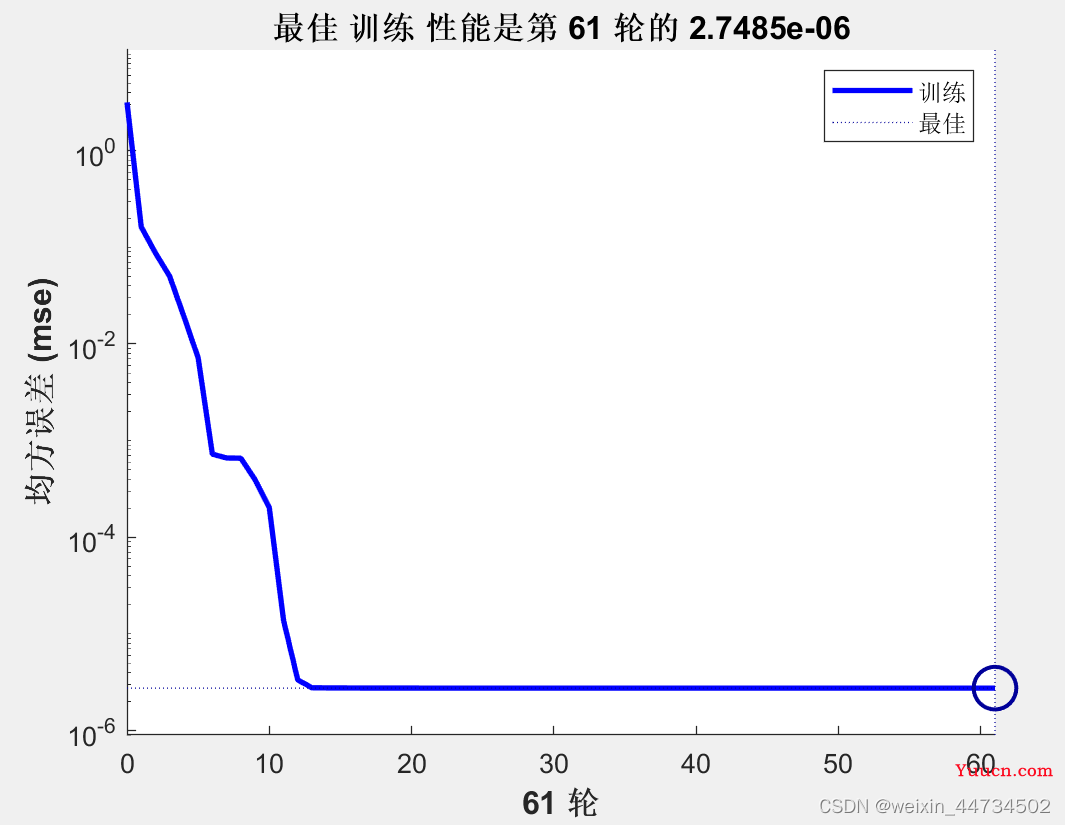
图3 BP神经网络训练误差曲线图
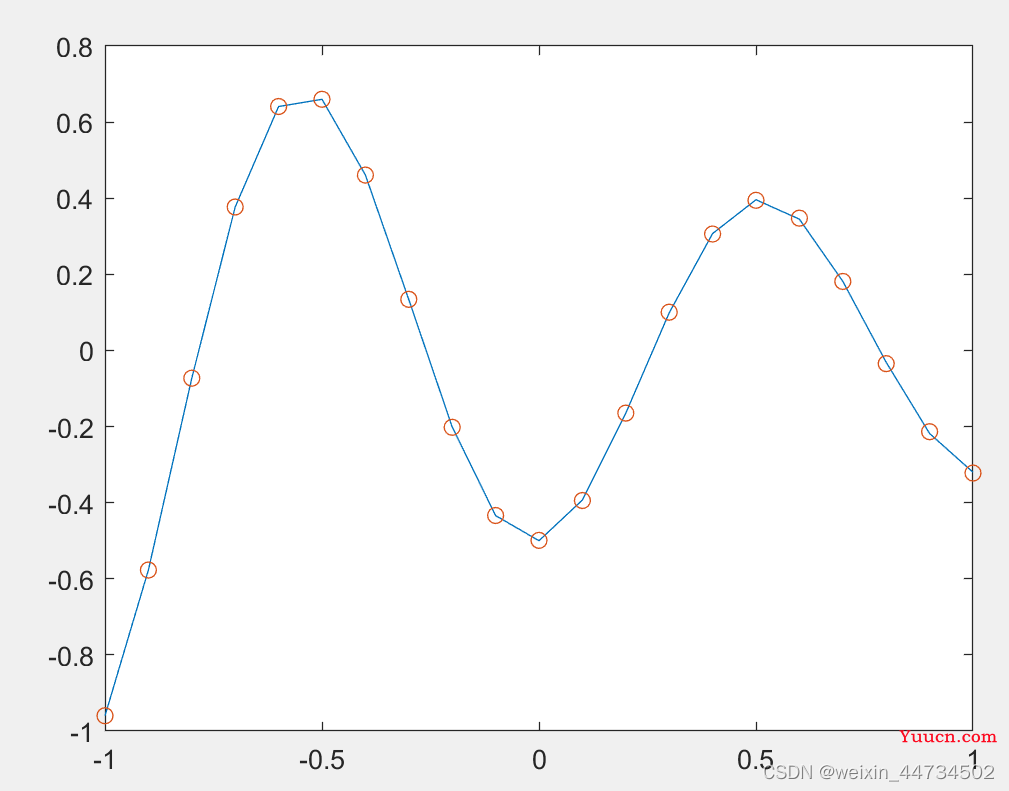
图4 训练后BP神经网络仿真图
在进行网络训练的时候小编发现了一个很有意思的事情,网络每次达到最佳训练次数都不同,这里是因为神经网络每次结果不同是因为初始化的权值和阈值是随机的,因为每次的结果不一样,才有可能找到比较理想的结果,找到比较好的结果后,用命令save filename net;保存网络,可使预测的结果不会变化,调用时用命令load filename net。
4.3 预测问题
例3 货运量预测问题请根据中国统计年鉴1990-2011年的各项数据,以国民生产总值、能源生产总值、进出口贸易额、社会消费品零售总额以及固定资产投资总额等5个指标作为主要因素,并利用BP神经网络预测货运总量。
1990-2011年的货运总量及主要因素部分数据
|
年份 |
货运总量 (万吨) |
国民生产总值(亿元) |
能源生产总值(万吨) |
进出口贸易额(亿元) |
社会消费品零售总额 |
固定资产投资总额 |
|
1990 |
970602 |
18718.3 |
103922 |
5560.1 |
8300.1 |
6955.81 |
|
1991 |
985793 |
21826.2 |
104844 |
7225.8 |
9415.6 |
9810.4 |
|
1992 |
1045899 |
26937.3 |
107256 |
9119.6 |
10993.7 |
12443.12 |
|
1993 |
1115902 |
35260 |
111059 |
11271 |
14270.4 |
14410.22 |
|
1994 |
1180396 |
48108.5 |
118729 |
20381.9 |
18622.9 |
17042.94 |
|
1995 |
1234938 |
59810.5 |
129034 |
23499.9 |
23613.8 |
20019.3 |
|
1996 |
1298421 |
70142.5 |
133032 |
24133.8 |
28360.2 |
22974 |
|
1997 |
1278218 |
78060.9 |
133460 |
26967.2 |
31252.9 |
24941.1 |
|
1998 |
1267427 |
83024.3 |
129834 |
26849.7 |
33378.1 |
28406.2 |
|
1999 |
1293008 |
88479.2 |
131935 |
29896.2 |
35647.9 |
29854.7 |
|
2000 |
1358682 |
98000.5 |
135048 |
39273.2 |
39105.7 |
32917.7 |
|
2001 |
1401786 |
108068.2 |
143875 |
42183.6 |
43055.4 |
37213.5 |
|
2002 |
1483447 |
119095.7 |
150656 |
51378.2 |
48135.9 |
43499.9 |
|
2003 |
1564492 |
134977 |
171906 |
70483.5 |
52516.3 |
55566.6 |
|
2004 |
1706412 |
159453.6 |
196648 |
95539.1 |
59501 |
70477.43 |
解:模型建立:利用BP神经网络进行预测。首先,根据输入/输出数据确定网络的结构。并确定训练数据来训练网络,使网络具有预测能力。然后,确定测试数据测试网络的预测性能。最后,根据训练好的网络预测货运总量。
由于本例输入数据为5维,输出为1维,所以BP神经网络结构为5-9-1结构。也就是说,输入层分别为国民生产总值、能源生产总值、进出口贸易额、社会消费品零售总额以及固定资产投资总额等5个主要因素的归一化数据,输出为货运总量,隐含层有9个节(可以根据情况调整)。并选取tansig为隐含层传递函数,线性函数f(x)=x为输出层传递函数。
已知有22年的数据,取前20年的数据作为训练数据训练网络。由于数据量较少,因此,将训练数据作为测试数据,来判定网络的预测性能,最后来预测2010和2011年两年的货运总量。
模型求解:根据BP神经网络原理,在Matlab中编程实现。
(1)数据处理:表数据存储在e4_3.xls中。按照上述分配数据的方式调用数据,并对数据进行归一化处理。数据归一化处理把所有数据都转化为[0,1]之间的数,其目的是消除数据间数量级差别,避免因为输入输出数据数量级差别较大而造成网络预测误差较大。归一化的方法很多,本例采用最大最小归一化方法,归一化函数采用Matlab自带函数mapminmax。该函数有多种形式,常用的方法如下:
[x1,ps] = mapminmax(x)
其中x是待归一化的数据,x1为归一化后的数据,ps是归一化后的结构体,包含了数据x的最大值、最小值和平均值等信息。对归一化后的数据x1进行反归一化处理的方法为:
x = mapminmax('reverse',x1,ps)
若需要利用数据x归一化后的结构体ps对新的数据y进行归一化处理,如神经网络中的测试数据和预测数据,其方法为:
y1 = mapminmax('apply',y,ps)
其中y1为数据y归一化后的数据,对y1反归一化处理方式同上。
(2)BP神经网络初始化:根据BP神经网络5-9-1结构,随机初始化BP神经网络权值和阈值。
(3)BP神经网络训练:用训练数据训练BP神经网络,并根据网络预测误差调整网络的权值和阈值。
(4)BP神经网络测试:用测试数据测试BP神经网络预测性能。
(5)BP神经网络预测:输入2010年和2011年主要因素,利用训练好的网络预测这两年的货运总量。
(6)预测结果:从测试数据的结果,BP神经网络测试的最大误差百分比约为4%,测试结果见图12-23,可认为BP网络具有良好的预测能力。2010年和2011年货运量预测结果分别为3133147万吨和3370948万吨,误差百分比分别为3.35%和8.82%,与实际结果比较接近
Matlab实现如下
clc;clear all %情况变量环境
[xdata,textdata]=xlsread('e4_3.xls'); %读取货运量数据
[n,m]=size(xdata);
Train_Num=20; %输入样本数量为20
Test_Num=Train_Num; %测试样本数量也是20
Sim_Num=2; %预测样本数量为6
%提取输入Input和输出Output数据
Input=[xdata(1:Train_Num,3) xdata(1:Train_Num,4) xdata(1:Train_Num,5) xdata(1:Train_Num,6) xdata(1:Train_Num,7)]';
Output=xdata(1:Train_Num,2)';
%%%数据归一化处理
[Inputn,In_ps]=mapminmax(Input,0,1); %输入数据归一化
[Outputn,Out_ps]=mapminmax(Output,0,1); %输出数据归一化
Train_Input=Inputn(:,1:Train_Num); %训练数据输入
Test_Input=Train_Input; %测试数据输入
Train_Output=Outputn(:,1:Train_Num); %训练数据输出
Test_Output=Train_Output; %测试数据输出
Input_Num=5; %输入节点个数
Hidd_Num=9; %中间层隐节点数量取9
Out_Num=1; %网络输出维度为1
MaxEpochs=50000; %最多训练次数为50000
lr=0.01; %学习速率为0.01
E0=0.45*10^(-2); %目标误差为0.45*10^(-2)
W1=0.5*rand(Hidd_Num,Input_Num)-0.1; %初始化输入层与隐含层之间的权值
B1=0.5*rand(Hidd_Num,1)-0.1; %初始化输入层与隐含层之间的阈值
W2=0.5*rand(Out_Num,Hidd_Num)-0.1; %初始化输出层与隐含层之间的权值
B2=0.5*rand(Out_Num,1)-0.1; %初始化输出层与隐含层之间的阈值
ErrHistory=[]; %给中间变量预先占据内存
for i=1:MaxEpochs
HiddenOut=logsig(W1*Train_Input+repmat(B1,1,Train_Num)); % 隐含层网络输出 9x5x5x20+9x20=9x20
NetworkOut=W2*HiddenOut+repmat(B2,1,Train_Num); % 输出层网络输出
Error=Train_Output-NetworkOut; % 实际输出与网络输出之差
SSE=sumsqr(Error) %能量函数(误差平方和)
ErrHistory=[ErrHistory SSE];
if SSE<E0,break, end %如果达到误差要求则跳出学习循环
% 以下是BP网络最核心的程序
% 它们是权值(阈值)依据能量函数负梯度下降原理所作的每一步动态调整量
Delta2=Error;
Delta1=W2'*Delta2.*HiddenOut.*(1-HiddenOut);
dW2=Delta2*HiddenOut';
dB2=Delta2*ones(Train_Num,1);
dW1=Delta1*Train_Input';
dB1=Delta1*ones(Train_Num,1);
%对输出层与隐含层之间的权值和阈值进行修正
W2=W2+lr*dW2;
B2=B2+lr*dB2;
%对输入层与隐含层之间的权值和阈值进行修正
W1=W1+lr*dW1;
B1=B1+lr*dB1;
end
HiddenOut=logsig(W1*Test_Input+repmat(B1,1,Test_Num)); % 隐含层输出最终结果
NetworkOut=W2*HiddenOut+repmat(B2,1,Test_Num); % 输出层输出最终结果
Test_Out=mapminmax('reverse',NetworkOut',Out_ps); % 还原网络输出层的结果,得到测试数据网络实际输出
Error=Test_Out-Output'; % 网络实际输出Test_Out与期望输出Output之间的误差
Error_bi=Error./Output'; % 网络实际输出与期望输出之间的误差比
%%%BP神经网络预测 输入为2010年和2011年主要因素
Sim_Input=[xdata(Train_Num+1:end,3) xdata(Train_Num+1:end,4) xdata(Train_Num+1:end,5) xdata(Train_Num+1:end,6) xdata(Train_Num+1:end,7)]';
Sim_Output=xdata(Train_Num+1:end,2)';
Sim_Input=mapminmax('apply',Sim_Input,In_ps);
HiddenOut=logsig(W1*Sim_Input+repmat(B1,1,Sim_Num)); % 隐含层输出最终结果
NetworkOut=W2*HiddenOut+repmat(B2,1,Sim_Num); % 输出层输出最终结果
Sim_Out=mapminmax('reverse',NetworkOut',Out_ps); % 还原网络输出层的结果
Error=Sim_Out-Sim_Output'; % 网络预测输出Sim_Out与期望输出Sim_Output之间的误差
baifenbi=Error./Sim_Output'; % 网络预测输出与期望输出之间的误差比
figure(1)
time1=1:Train_Num;
plot(time1+1989,Test_Out,'r-o',time1+1989,Output(1:Train_Num),'b--+')
legend('网络测试输出货运量','实际货运总量');
xlabel('年份');ylabel('货运总量/万吨');
% figure(2)
% time2=Train_Num+1:22;
% plot(time2+1989,Sim_Out,'r-o',time2+1989,Sim_Output,'b--+')
最佳训练性能是第 775 轮的 0.00099919 如图5
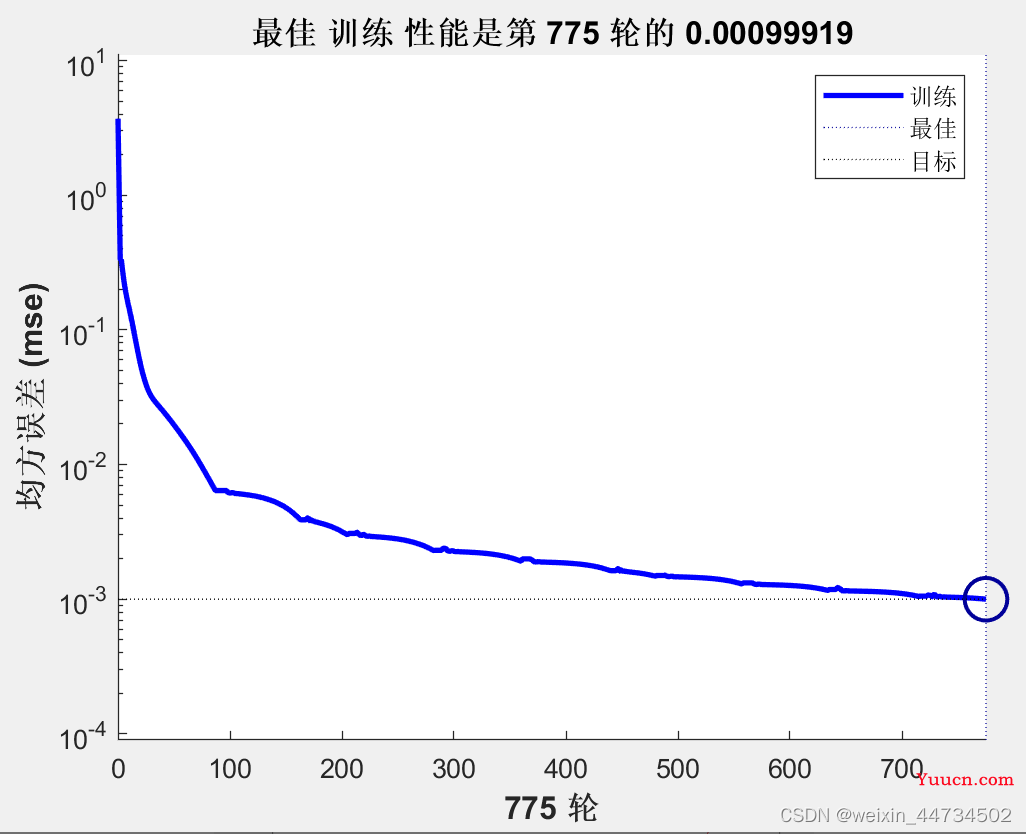
图5
BP神经网络测试结果如图6
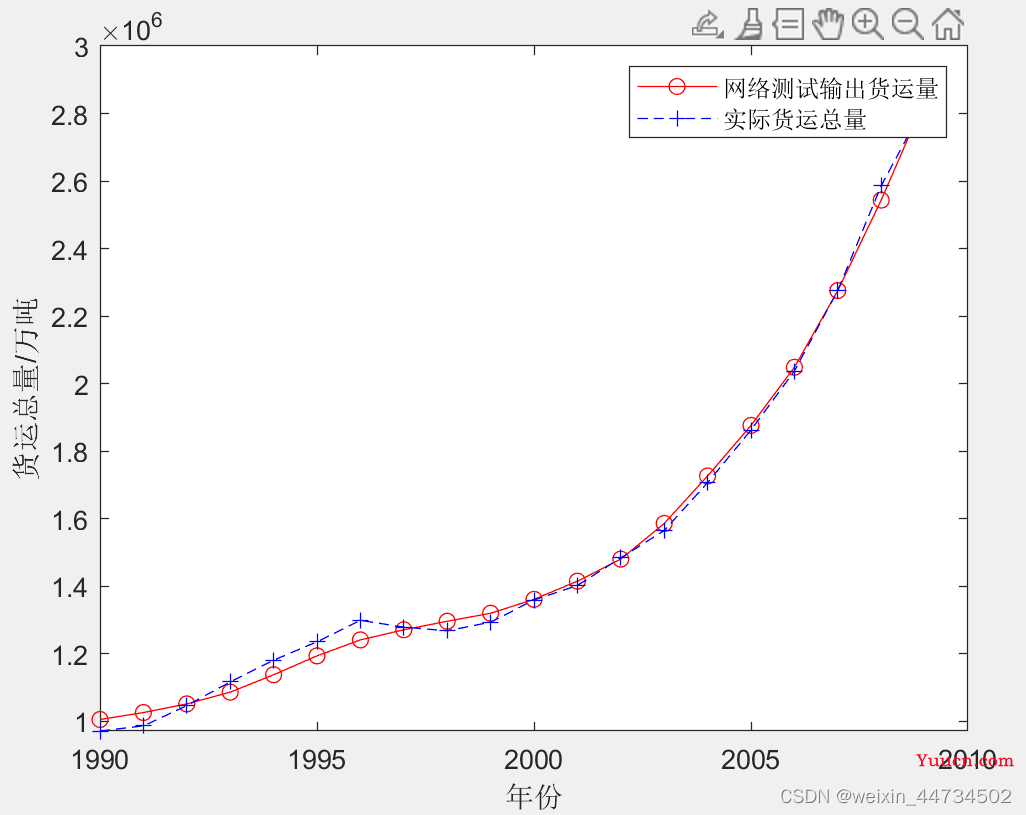
图6
预测得到的2010年和2011年货运总量数据如图7,红色线表示预测值
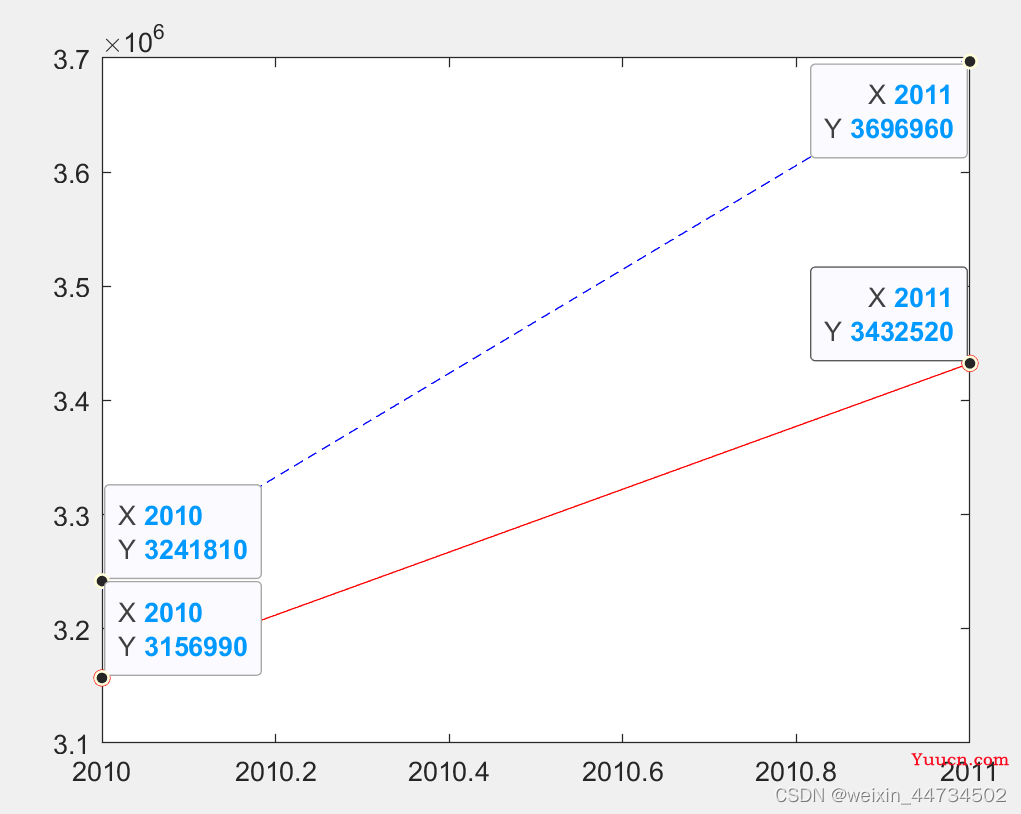
图7
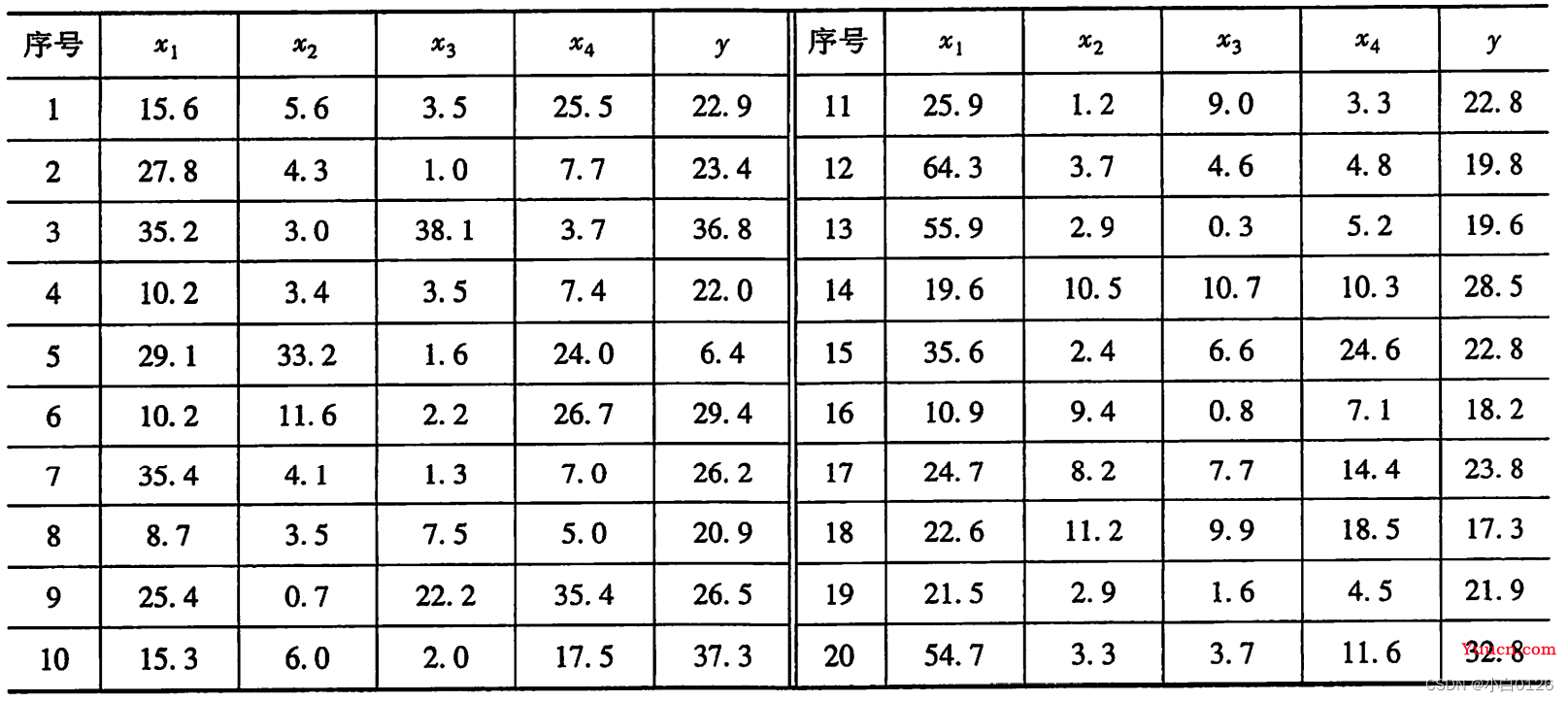
例4 现有某水库径流资料和相应前期四个预报因子实测数据见下表,其中4个预报因子分别为水库上一年11月和12月的总降雨量x1,当年1,2,3月的降雨量x2,x3,x4。本例将这四个预报因子作为输入,年径流量作为输出,构成四个输入一个输出的网络,将前19个实测数据作为训练样本集,后一个实测数据作为预测检验样本。
网络的训练
利用Matlab提供的神经网络工具箱实现人工神经网络功能十分方便。由于年径流预报中自变量有四个,因变量有1个,输入神经元个数取为4,输出神经元个数取为1,中间隐含层神经元个数,BP神经网络需要根据经验取定,RBF神经网络会在训练过程中自适应取定。
BP神经网络存在一些缺点,如收敛速度慢,网络易陷入局部最小值,学习过程常常发生振荡。对于本案例的预测,BP神经网络隐含层个数取为4时计算结果相对稳定,隐含层个数取为其他值时,运行结果特别不稳定,每一次的运行结果相差很大。
利用Matlab工具箱,求得第20个样本点,RBF神经网络的预测值为26.7693,相对误差为18.39%,BP神经网络的运行结果每次都有很大的不同,通过计算结果可以看出,RBF神经网络模型的预测结果要好于BP神经网络模型的预测结果。
Matlab代码如下
clc, clear
a=load('l_4.txt'); %把表中的数据保存到文本文件l_4.txt
a=a'; %注意神经网络的数据格式,不要将转置关系搞错
P=a([1:4],[1:end-1]); [PN,PS1]=mapminmax(P); %自变量数据规格化到[-1,1]
T=a(5,[1:end-1]); [TN,PS2]=mapminmax(T); %因变量数据规格化到[-1,1]
net1=newrb(PN,TN) %训练RBF网络
x=a([1:4],end); xn=mapminmax('apply',x,PS1); %预测样本点自变量规格化
yn1=sim(net1,xn); y1=mapminmax('reverse',yn1,PS2) %求预测值,并把数据还原
delta1=abs(a(5,20)-y1)/a(5,20) %计算RBF网络预测的相对误差
net2=feedforwardnet(4); %初始化BP网络,隐含层的神经元取为4个(多次试验)
net2 = train(net2,PN,TN); %训练BP网络
yn2= net2(xn); y2=mapminmax('reverse',yn2,PS2) %求预测值,并把数据还原
l_4.txt
15.6 5.6 3.5 25.5 22.9
27.8 4.3 1.0 7.7 23.4
35.2 3.0 38.1 3.7 36.8
10.2 3.4 3.5 7.4 22.0
29.1 33.2 1.6 24.0 6.4
10.2 11.6 2.2 26.7 29.4
35.4 4.1 1.3 7.0 26.2
8.7 3.5 7.5 5.0 20.9
25.4 0.7 22.2 35.4 26.5
15.3 6.0 2.0 17.5 37.3
25.9 1.2 9.0 3.3 22.8
64.3 3.7 4.6 4.8 19.8
55.9 2.9 0.3 5.2 19.6
19.6 10.5 10.7 10.3 28.5
35.6 2.4 6.6 24.6 22.8
10.9 9.4 0.8 7.1 18.2
24.7 8.2 7.7 14.4 23.8
22.6 11.2 9.9 18.5 17.3
21.5 2.9 1.6 4.5 21.9
54.7 3.3 3.7 11.6 32.8
五、神经网络模型优劣势
BP神经网络无论在网络理论还是在性能方面已比较成熟。其突出优点就是具有很强的非线性映射能力和柔性的网络结构。网络的中间层数、各层的神经元个数可根据具体情况任意设定,并且随着结构的差异其性能也有所不同。但是BP神经网络也存在以下的一些主要缺陷。
①学习速度慢,即使是一个简单的问题,一般也需要几百次甚至上千次的学习才能收敛。
②容易陷入局部极小值。
③网络层数、神经元个数的选择没有相应的理论指导。
④网络推广能力有限。