前言
脑电图作为目前研究最为广泛的认知大脑的方式之一,其无创性、便携性、廉价等优点都表明该方式具有巨大的发展空间。但是由于颅骨和头皮对于电信号的传输影响,从头皮采集的电信号往往混杂着非常多的噪声,并且有效信息又非常少,所以对于去处噪声的算法的要求非常高。本文将对EEG降噪的算法做作一些介绍。
EEG信号采集及噪声来源分析
EEG信号是极其微弱的电压信号(0.5~100
μ
\mu
μV),EEG信号采集指将采集电极按照国际规定点放置于头皮表面,通过探测各点电位差达到采集脑电信号的目的。
目前采集信号的电极有两种,分别是湿电极、干电极,通过是否使用导电膏来区分。
EEG记录的是不同电极之间的电位差,因此根据参考电极的不同还可以分为单导联和双导联采集,如下图。
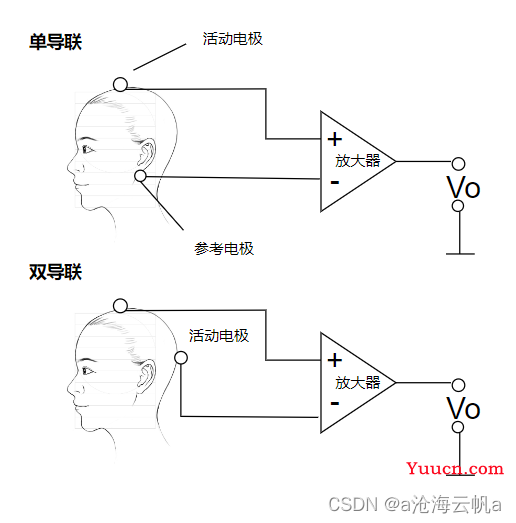
EEG是一种复杂的生物电信号,他反映了大脑的工作状态,并且可以被读取识别。其频率范围从0.01Hz到100Hz左右,可以划分为五个频带。
| 频带名称 | 频带范围(Hz) | 介绍 |
|---|---|---|
| delta | <4 | 通常出现于成人的深度睡眠时期 |
| theta | 4-8 | 通常出现于放松状态或者冥想状态 |
| alpha | 8-13 | 当清醒的人处于放松状态时会出现 |
| beta | 13-30 | 通常出现于注意力集中的状态 |
| gamma | 30-50 | 通常出现于人体十分亢奋的状态 |
EEG信号的噪声主要来自于仪器和人体,仪器造成的噪声可以通过严格记录和提升设备记录精确度去除。真正较为复杂的是对来自于人体的生理伪影,如眼球运动、眨眼、心跳活动、肌肉活动等。下图是EEG信号中的生理伪影。
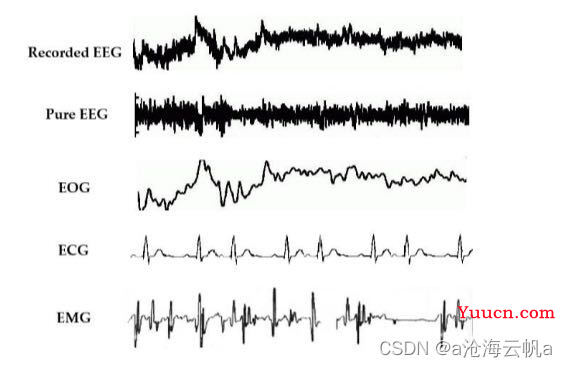
眼部伪影(EOG)是对EEG影响最为显著的信号,源于眼球运动和眨眼的信号在头皮上的传播,其频率和EEG频率类似但振幅较大。
心脏活动会导致血管的收缩与扩张,对位于头部血管附近的电极产生污染信号,污染与EEG信号类似,较难去除,但可以同时记录ECG信号作为参考波形去除此类影响。
肌肉活动对EEG的影响源于不同类型的肌肉群产生的电信号,受试者的任何肌肉活动都会对信号造成污染,包括说话、嗅、吞咽等,这是不可避免的。肌肉活动产生的伪影分布的频带范围也十分广泛从0Hz到200Hz均有分布,好在该污染信号与EEG在时间和空间上具有独立性,所以独立成分分析或许是去除该污染的合适方法。
单一EEG降噪算法
回归方法
回归方法是EEG去除伪影的传统方法,该方法假设每个通道的EEG都是干净的EEG数据和一定比例的伪影的累积和,如下,下标H和V表示噪声水平通道和垂直通道的记录。
E
E
G
r
e
c
o
r
d
=
E
E
G
p
u
r
e
+
{
γ
1
F
(
n
o
i
s
e
1
H
)
+
δ
1
F
(
n
o
i
s
e
1
V
)
}
+
{
γ
2
F
(
n
o
i
s
e
2
H
)
+
δ
2
F
(
n
o
i
s
e
2
V
)
}
+
…
EEG_{record}=EEG_{pure}+\{\gamma_1F(noise1_H)+\delta_1F(noise1_V)\}+\{\gamma_2F(noise2_H)+\delta_2F(noise2_V)\}+\dots
EEGrecord=EEGpure+{γ1F(noise1H)+δ1F(noise1V)}+{γ2F(noise2H)+δ2F(noise2V)}+…
γ
\gamma
γ和
δ
\delta
δ取决于噪声与EEG之间的传输系数,回归方法的降噪过程就是获得最优的
γ
\gamma
γ和
δ
\delta
δ。这种方法可以在时域上实现使用,也可以在频域上使用。
回归方法简化了模型而且降低了计算要求,不过,这个方法需要较好的获得噪声源信号如EOG和EMG信号,这往往是比较困难的。但是,回归方法依旧是评估新方法的金标准。
小波变换
小波变换可以把原信号从时域转换到时频域,相对于傅立叶变换它具有良好的时频特性,在分析弱信号和非平稳信号时具有天然的优势。小波变换通过选择恰当的母小波
ψ
(
t
)
\psi(t)
ψ(t)的尺度
j
j
j和
k
k
k将原始信号进行分解。分解后的信号不仅具有代表尺度变化的信息
(
j
)
(j)
(j),还具有位置变化的信息
(
k
)
(k)
(k)。
ψ
j
,
k
(
t
)
=
2
j
2
ψ
(
2
j
t
−
k
)
\psi_{j,k}(t)=2^{j \over2}\psi(2^jt-k)
ψj,k(t)=22jψ(2jt−k)
小波变换用数学表示为:
W
ψ
=
<
f
,
ψ
j
,
k
>
W_\psi=<f,\psi_{j,k}>
Wψ=<f,ψj,k>
<
>
<>
<>表示点积,
f
f
f为原始信号。
当然,上述知识连续信号的小波变换,离散信号的小波变换也是类似的,这里仅作小波变换的简单介绍。实际上,要是想真正的理解小波变换还是有一定的难度的,这里只是简述了基本思想,完整的小波变换至少还有尺度函数需要去理解,这也是小波分析的重点。
盲源分离(BSS)
盲源分离技术是在未知系统传递函数、源信号混合系数及概率分布的情况下,仅利用源信号之间相互独立这一条件,从采集的信号中分离出各独立源信号的技术。
盲源分离任务来自于Colin Cherry提出的鸡尾酒会问题———“为什么人类在多个人同时说话时能够选择性的聆听,而机器不行?”,每个人说话产生的都是相互独立的源信号,我们的大脑具有强大的盲源分离能力和注意机制帮助我们选择性的聆听某人在说的话。
BSS方法包括多种无监督机器学习算法,其一般描述如下:设
X
X
X为从头皮获得的观察信号,
S
S
S为原始信号和噪声源信号,这些信号通过未知矩阵
A
A
A线性混合得到:
X
=
A
S
X=AS
X=AS
BSS算法则是如下表示:
U
=
W
X
U=WX
U=WX
U
U
U是对源信号的估计,
W
W
W是
X
X
X的解混矩阵。得到U后去除代表伪影的分量并重构脑电数据就可以得到降噪后的脑电信号了,下面是一些代表性的算法。
主成分分析
主成分分析(PCA)是最简单的且应用最为广泛的盲源分离技术之一,算法基于协方差矩阵的特征值实现。算法流程如下:
- 将原始数据按列组成
n
n
n行
m
m
m列的矩阵
X
X
X,然后
X
X
X中每一维的数据减去该维均值得到矩阵
X
′
X'
X′。(样本“中心化”) - 计算样本的协方差矩阵
C
=
1
m
X
′
X
′
T
C={1\over m}X'X'^T
C=m1X′X′T - 使用奇异值分解求出协方差矩阵的特征值和对应的特征向量。
- 按特征值大小将对影特征向量排列成矩阵,取
k
k
k行组成矩阵
P
P
P。 - 最后计算
Y
=
P
X
Y=PX
Y=PX得到降维后的数据。
PCA方法的计算效率是高于线性线性方法的,而且不需要额外信息,但是伪影和EEG不相关的要求往往是难以满足的,而且当漂移电位与EEG数据相似时,PCA几乎无法分离干扰,所以后续的研究更倾向于独立成分分析(ICA)等算法。
独立成分分析
独立成分分析假设信号源是大脑信号和伪影信号的瞬时线性混合,并且可以将观察到的信号分解为独立分量。ICA可以说是PCA的扩展,在源信号彼此统计独立且瞬时混合、观测维数大于等于源信号维数、各源中至多有一个是高斯的的条件下表现更加出色。对于观测的EEG数据来说,EEG与眼动、眨眼、心跳活动等信号显然是统计独立的,容积容积传导也是线性的,只是数据采集通常不是瞬时线性混合的。
典型相关分析
不同于ICA使用高阶统计量,典型相关分析(CCA)使用二阶统计量,大幅度缩短了计算时间。CCA通过最大化两个数据之间的相关性来发现两个多维随机变量之间的线性关系,CCA还考虑了源信号的自相关性,这与ICA考虑相同样本值的统计分布相类似但计算复杂度更小。
该算法常用于去除肌肉活动伪影,效果优于ICA。
源成像方法
#没太看懂这个方法,采用论文里的解释进行介绍。
EEG源成像(ESI)是一种基于模型的成像技术,结合EEG数据的时间和空间分量,查找头皮记录到的点位的来源。ESI中有两个基本问题:正向和反向问题,头皮记录的等效分布偶极子层反演是一种线性反演,可以用最小范数法求解,但实践中使用了各种正则或加权最小范数法求解。其目的是从脑电图中重建出等效分布源,随后使用主成分分析去除第一分量,使用剩余分量重建无伪影EEG数据。
经验模态分解
经验模态分解(EMD)是一种非平稳和非线性信号处理的启发式技术。EMD算法将信号分解为一组振幅-频率调制的分量,称为本征模函数(IMF)。IMF需要满足极值个数与过零点个数相等或相差至多一个,且由极值和极值定义的包络线的均值必须为零。该算法无需预先设定任何基函数,仅依据自身的时间尺度特征进行信号分解。分解过程如下:
设原始数据为
x
[
n
]
x[n]
x[n]
- 找到信号所有的极大值与极小值,并分别使用三次采样插值连接它们,获得上包络
u
[
n
]
u[n]
u[n]和下包络
l
[
n
]
l[n]
l[n]。 - 计算平均值
μ
[
n
]
=
(
u
[
n
]
+
l
[
n
]
)
/
2
\mu[n]=(u[n]+l[n])/2
μ[n]=(u[n]+l[n])/2,并从原始值中减去
b
[
n
]
=
x
[
n
]
−
μ
[
n
]
b[n]=x[n]-\mu[n]
b[n]=x[n]−μ[n]。 - 根据预设条件判断
b
[
n
]
b[n]
b[n]是否为IMF。 - 如果不是,用
b
[
n
]
b[n]
b[n]代替
x
[
n
]
x[n]
x[n],直到
b
[
n
]
b[n]
b[n]满足判据,则
b
[
n
]
b[n]
b[n]就是需要提取的IMF,记
b
k
[
n
]
b_k[n]
bk[n]。 - 每获得一阶IMF就从原信号中减去它,直到剩余部分
r
[
n
]
r[n]
r[n]为单调序列或常值序列。
原始信号就可以被分解为:
x
[
n
]
=
∑
k
=
1
m
b
k
[
n
]
+
r
[
n
]
x[n]=\sum_{k=1}^mb_k[n]+r[n]
x[n]=k=1∑mbk[n]+r[n]
确定分解后的信号后就可以选择并去除伪影分量,然后使用新的IMF重构出纯净的EEG数据。
滤波方法
在消除噪声的过程中也使用了很多的滤波方法,如自适应滤波、维纳滤波、贝叶斯滤波等,不同的滤波方式采用的优化原理也不同。
自适应滤波
自适应滤波的基本原理是根据优化算法迭代调整权重,量化主要输入中的噪声,并将其滤除,如下图。
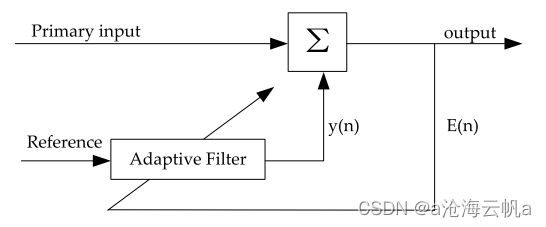
为了获得纯净的信号,通常会使用最小均方、递归最小二成算法等优化算法来帮助自适应滤波器更新其权重。其缺点是需要一个额外的参考输入。
维纳滤波
维纳滤波同样也是一种最佳滤波方法,不同的是,维纳滤波是一种线性统计滤波技术,用于估计真实的EEG数据。维纳滤波目的是构造一个线性时不变滤波器最小化真实EEG数据与估计信号的均方误差,该滤波器通过估计测量信号和伪影信号的功率谱密度构造。维纳滤波摆脱了参考信号的束缚,但也同时增加了计算复杂度。
拓扑数据分析方法
拓扑数据分析(TDA)是一种新兴的EEG数据分析方法,它有非常多的优点,研究发现人类大脑处理外界信号的方式也有诸多的拓扑变换方法。拓扑特征是鲁棒的,它不会改变原始数据的特征。TDA可以捕捉全局甚至更高维度的特征。在分析网络结构时,不会因为节点之间的距离而忽视两节点的连接。
目前在EEG分析中使用TDA的方式有三种,一是直接应用于EEG信号,二是应用于连接网络,三是应用于相空间。
遗憾的是TDA在理论和应用都与上述方法存在很大差距,我也只能做简单介绍。
混合去噪方法
单一的去噪方法在使用时通常都是有缺陷的,因此尝试组合一些单一降噪方法可以获得充分利用每种方法的优势。下面列举一些混合方法,不做详细展开介绍。
-
经验模态分解—盲源分离

-
小波变换—盲源分离

-
盲源分离—支持向量机
