这是一篇ICLR2023 top 5%论文

论文链接：https://openreview.net/pdf?id=vSVLM2j9eie
代码：https://github.com/Thinklab-SJTU/Crossformer

1. Multivariate Time Series Forecasting

MTS，多变量时序数据预测。利用MTS的历史值可以预测其未来的趋势，例如心电图（ECG），脑电图（EEG）脑磁图(MEG)的诊断以及系统监测等等都是固有的多变量问题。该任务数据每个实例序列拥有多个维度，是一个d维向量和m个观测值(时间序列)的列表，如下所示数据（借鉴自综述论文：《The great multivariate time series classification bake off: a review and experimental evaluation of recent algorithmic advances》）

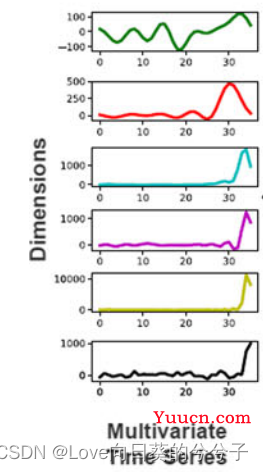
2. 动机

MTS的核心额外复杂性在于，区别性特征可能存在于维度之间的相互作用中，而不仅仅存在于单个序列中的自相关性中。标准的Transformer中核心self-attention可能仅仅建模了单个序列的自相关性，忽略了跨维度的依赖关系。

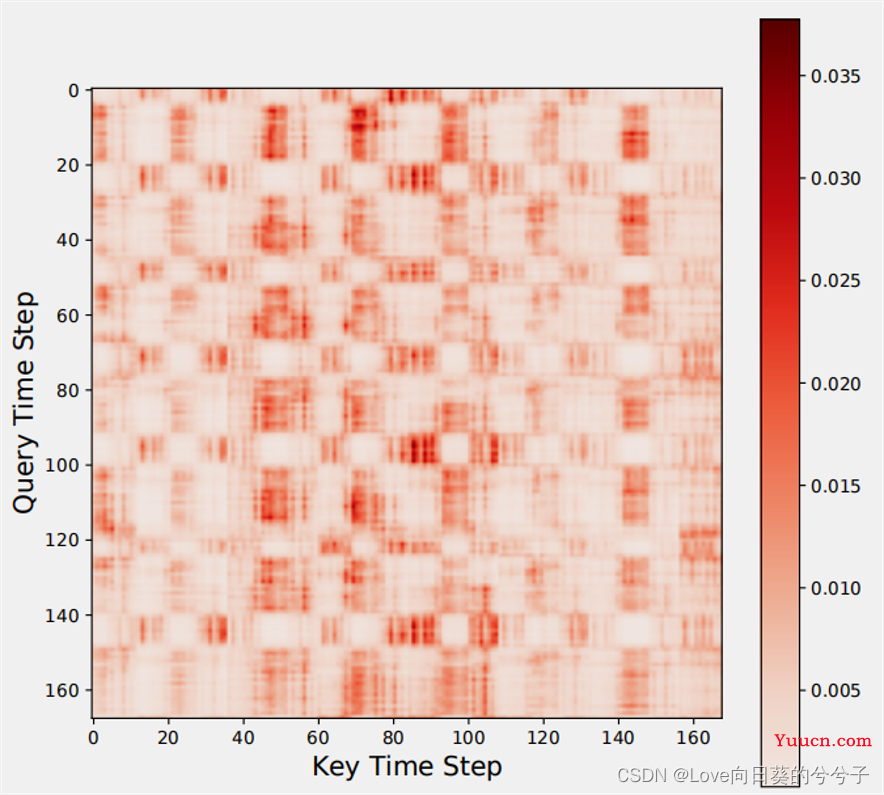
此外，如下图所示，当数据序列很长时，计算复杂性高，但是可以观察到，接近的数据点具有相似的注意权重！

基于此，作者提出一个分层encoder-decoder框架Crossformer.

3. Crossformer

目标：输入一段历史序列
x
1
:
T
∈
R
T
×
D
x_{1:T} \in \mathbb{R}^{T\times D}
x1:T​∈RT×D，预测未来的一段序列
x
T
+
1
:
T
+
τ
∈
R
τ
×
D
x_{T+1:T+\tau} \in \mathbb{R}^{\tau \times D}
xT+1:T+τ​∈Rτ×D.

3.1 Hierarchical Encoder-Decoder

作者提出一个新的层次Encoder-Decoder的架构，如下所示，由左边encoder（灰色）和右边decoder（浅橘色）组成。其主要包含Dimension-Segment-Wise (DSW) embedding，Two-Stage Attention (TSA)层和Linear Projection。

• Dimension-Segment-Wise (DSW) embedding：为了将输入
  x
  1
  :
  T
  ∈
  R
  T
  ×
  D
  x_{1:T} \in \mathbb{R}^{T\times D}
  x1:T​∈RT×D进行分segment，从而减少计算复杂性。如果最后每个序列要分成$L$个segment，每个序列
  d
  m
  o
  d
  e
  l
  d_{model}
  dmodel​的通道数，则最后的输入记为：
  Z
  ∈
  R
  L
  ×
  D
  ×
  d
  m
  o
  d
  e
  l
  Z \in \mathbb{R}^{L \times D \times d_{model}}
  Z∈RL×D×dmodel​.
• Two-Stage Attention (TSA)层：捕获cross-time和cross-dimension依赖关系。替待原来的self-attention在encoder和decoder中的位置。
• Linear Projection：应用于每一个decoder层的输出，以产生该层的预测。对各层预测结果进行求和，得到最终预测结果
  x
  T
  +
  1
  ：
  T
  +
  τ
  p
  r
  e
  d
  x^{pred}_{T+1：T+\tau}
  xT+1：T+τpred​.
  
  下面主要讲解DSW和TSA如何实现的！

3.2 Dimension-Segment-Wise embedding (DSW)

输入
x
1
:
T
∈
R
T
×
D
x_{1:T} \in \mathbb{R}^{T\times D}
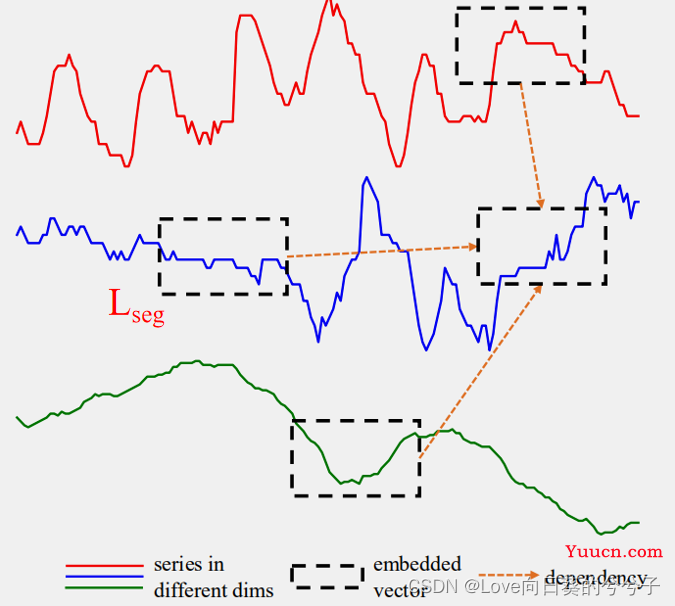
x1:T​∈RT×D，表明输入包含$T$个序列，每个序列有$D$个维度。如下所示，如果我们分的每个segment的长度为
L
s
e
g
L_{seg}
Lseg​，则每个序列中可以划分出
T
L
s
e
g
\frac{T}{L_{seg}}
Lseg​T​个segment，每个序列有$D$个维度，则整个输入共包含
T
L
s
e
g
×
D
\frac{T}{L_{seg}} \times D
Lseg​T​×D个segment，故
x
1
:
T
x_{1:T}
x1:T​可以记为：
x
1
:
T
=
{
x
i
,
d
(
s
)
∣
1
≤
i
≤
T
L
s
e
g
,
1
≤
d
≤
D
}
x_{1:T}=\{x^{(s)}_{i,d}|1\le i \le \frac{T}{L_{seg}}, 1 \le d \le D \}
x1:T​={xi,d(s)​∣1≤i≤Lseg​T​,1≤d≤D}。在$d$维度中的第$i$个segment的size记为
x
i
,
d
(
s
)
∈
R
1
×
L
s
e
g
x^{(s)}_{i,d} \in \mathbb{R}^{1 \times L_{seg}}
xi,d(s)​∈R1×Lseg​，然后使用线性投影和位置嵌入将每个段嵌入到一个向量中：

其中
h
i
,
d
∈
R
d
m
o
d
e
l
h_{i,d} \in \mathbb{R}^{d_{model}}
hi,d​∈Rdmodel​，
E
∈
R
d
m
o
d
e
l
×
L
s
e
g
E \in \mathbb{R}^{d_{model} \times L_{seg}}
E∈Rdmodel​×Lseg​表示可学习的映射矩阵。
E
i
,
d
(
p
o
s
)
∈
R
d
m
o
d
e
l
E^{(pos)}_{i,d} \in \mathbb{R}^{d_{model}}
Ei,d(pos)​∈Rdmodel​表示在$(i,d)$位置的可学习位置嵌入。

最后，可以获得一个2D的向量数组
H
=
{
h
i
,
d
∣
1
≤
i
≤
T
L
s
e
g
,
1
≤
d
≤
D
}
∈
R
T
L
s
e
g
×
D
×
d
m
o
d
e
l
H=\{ h_{i,d}|1 \le i \le \frac{T}{L_{seg}},1 \le d \le D \} \in \mathbb{R}^{\frac{T}{L_{seg}} \times D \times d_{model}}
H={hi,d​∣1≤i≤Lseg​T​,1≤d≤D}∈RLseg​T​×D×dmodel​.

3.3 Two-Stage Attention (TSA)

由上可得输入现在为：
H
∈
R
T
L
s
e
g
×
D
×
d
m
o
d
e
l
H \in \mathbb{R}^{\frac{T}{L_{seg}} \times D \times d_{model}}
H∈RLseg​T​×D×dmodel​，为了方便，记
L
=
T
L
s
e
g
L=\frac{T}{L_{seg}}
L=Lseg​T​，则输入为
H
∈
R
L
×
D
×
d
m
o
d
e
l
H \in \mathbb{R}^{L \times D \times d_{model}}
H∈RL×D×dmodel​。TSA主要由cross-time stage和
cross-dimension stage组成，如下图所示。

• Cross-Time Stage
  对于每个维度，包含所有时间序列。因此，对于$d$维度
  Z
  :
  ,
  d
  ∈
  R
  L
  ×
  d
  m
  o
  d
  e
  l
  Z_{:,d} \in \mathbb{R}^{L \times d_{model}}
  Z:,d​∈RL×dmodel​上，cross-time依赖关系可记为：
  
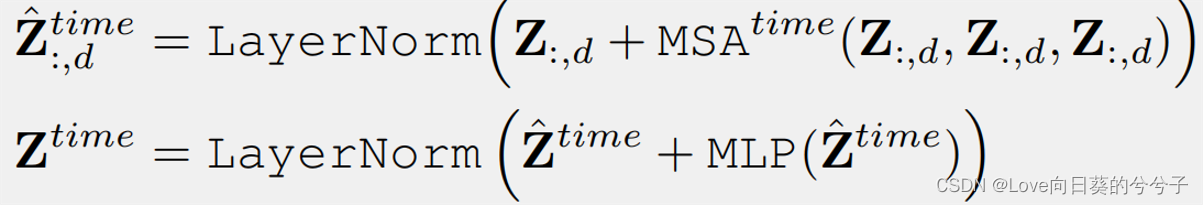
  其中$1\le d\le D$，所有维度共享MSA（multi-head self-attention）.
• Cross-Dimension Stage
  对于每个时间点，包含所有维度。因此，对于第$i$时间点
  Z
  i
  ,
  :
  t
  i
  m
  e
  ∈
  R
  D
  ×
  d
  m
  o
  d
  e
  l
  Z^{time}_{i,:} \in \mathbb{R}^{D \times d_{model}}
  Zi,:time​∈RD×dmodel​
  1）如果使用标准Transformer进行，如下图所示，可以很容易得到复杂性为
  O
  (
  D
  2
  )
  \mathcal{O}(D^2)
  O(D2)！总共有$L$个时间segment，因此总复杂性为
  O
  (
  D
  2
  L
  )
  \mathcal{O}(D^2L)
  O(D2L).
  
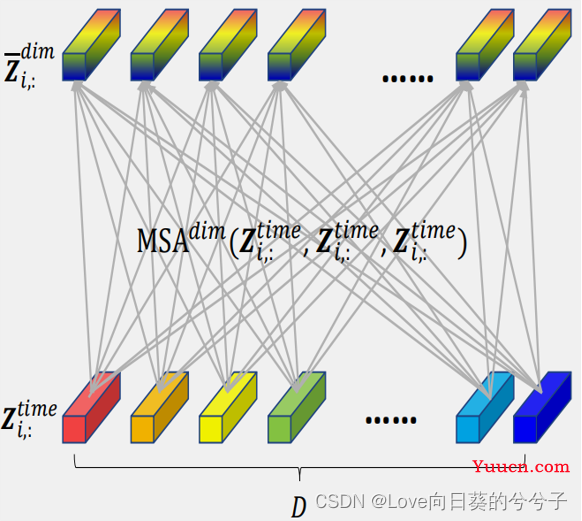
  2）作者引入router机制，每个时间点共享。如下图所示，
  R
  i
  ,
  :
  ∈
  R
  c
  ×
  d
  m
  o
  d
  e
  l
  R_{i,:} \in \mathbb{R}^{c×d_{model}}
  Ri,:​∈Rc×dmodel​ ($c$是常数)是作为路由器的可学习向量，作为第一个MSA的query.
  
  
  B
  i
  ,
  :
  ∈
  R
  c
  ×
  d
  m
  o
  d
  e
  l
  B_{i,:} \in \mathbb{R}^{c×d_{model}}
  Bi,:​∈Rc×dmodel​，作为第二个MSA的key和value.
  
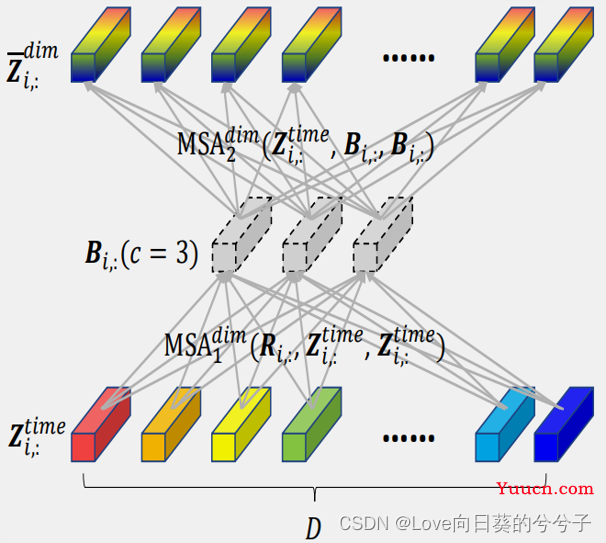
  由上可知，第一个MSA复杂性为$\mathcal{O}(cDL)$，第二个MSA也是如此，因此，最终复杂性为$\mathcal{O}(2cDL)$，其中$2c$为常量，记复杂性变为$\mathcal{O}(DL)$!!

4 实验

• SOTA方法对比
  
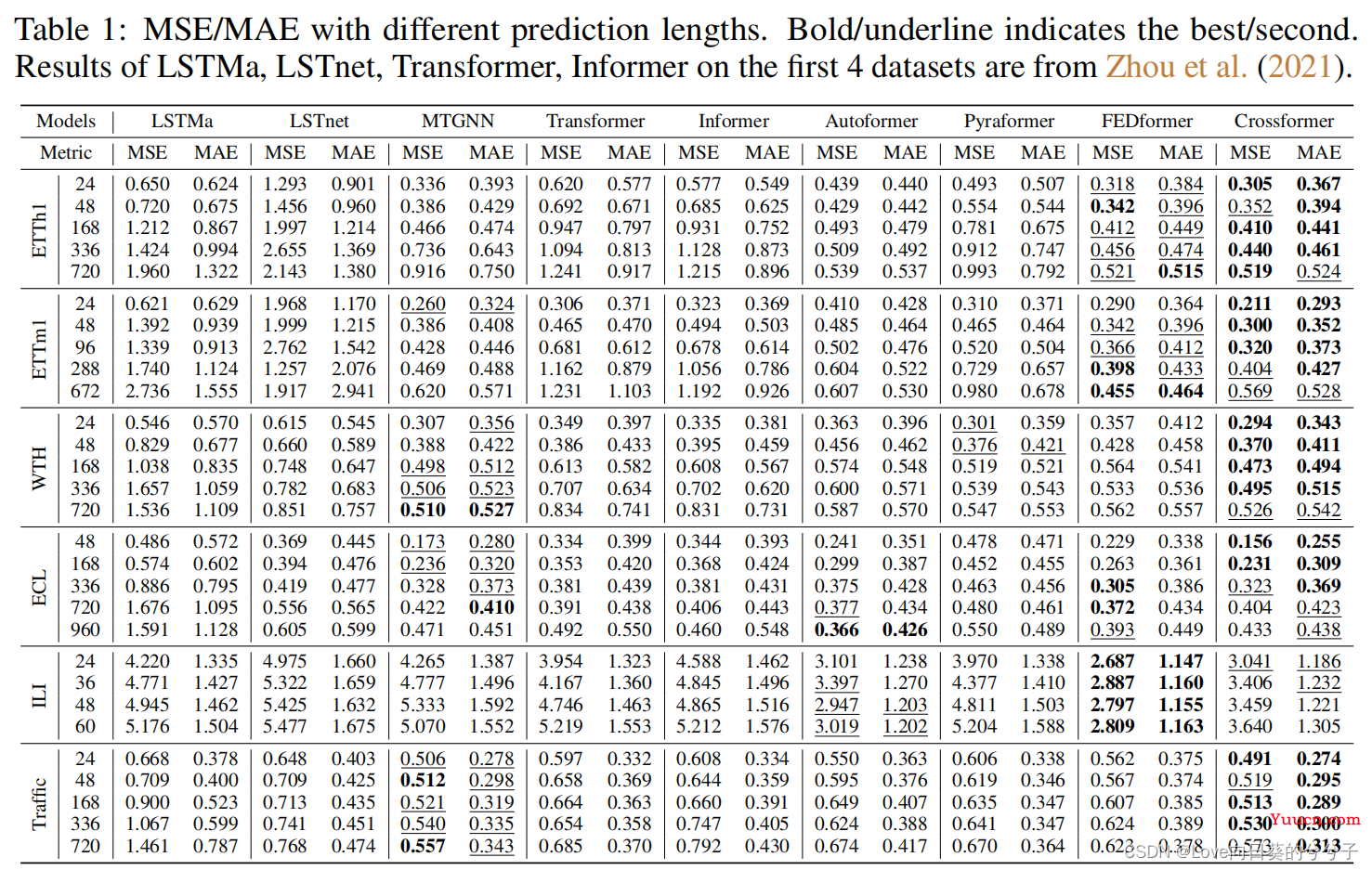
  更多对比方法：
  

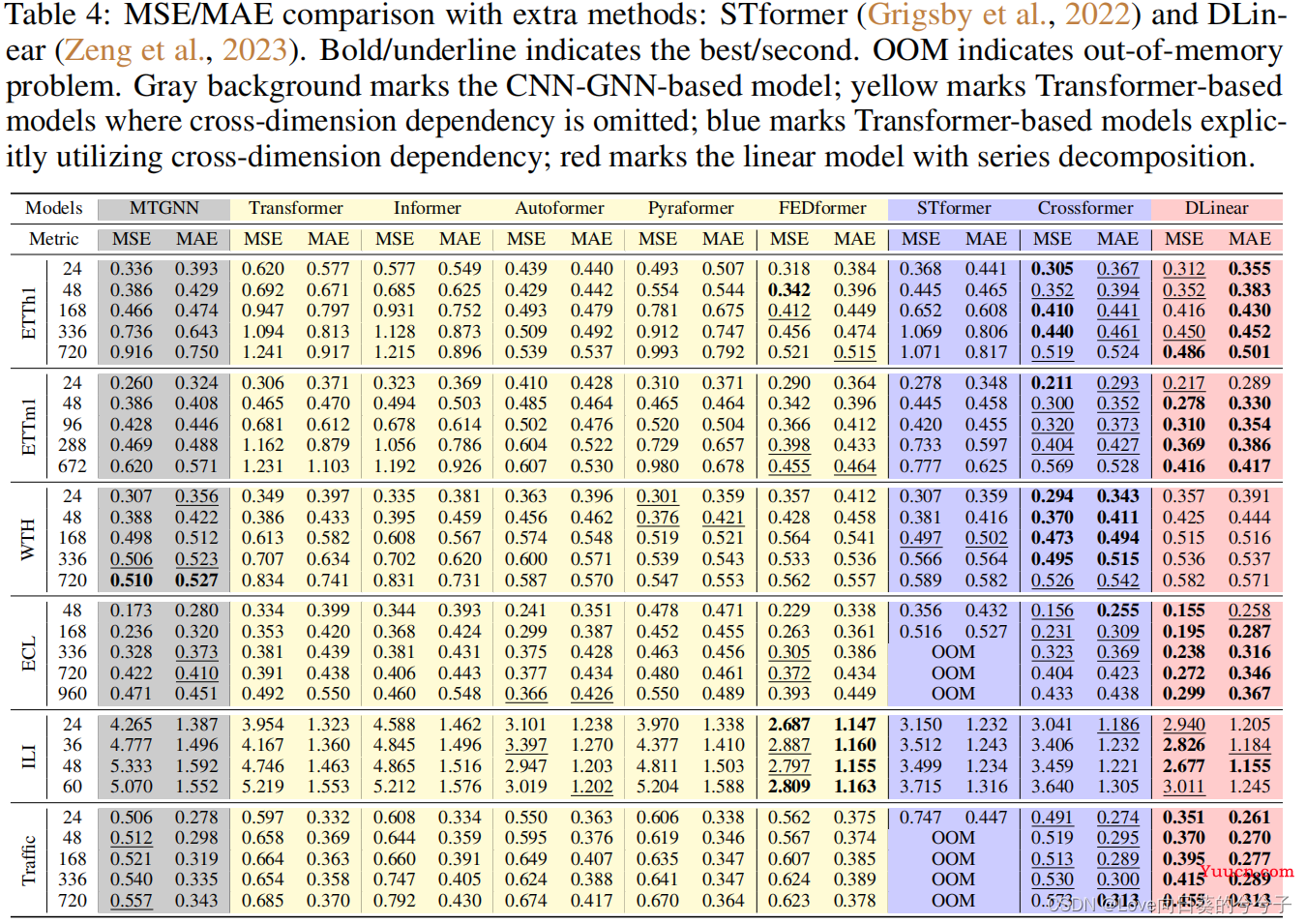
• 消融实验
  
  

• 参数分析
  

• 复杂性分析

• 可视化
  

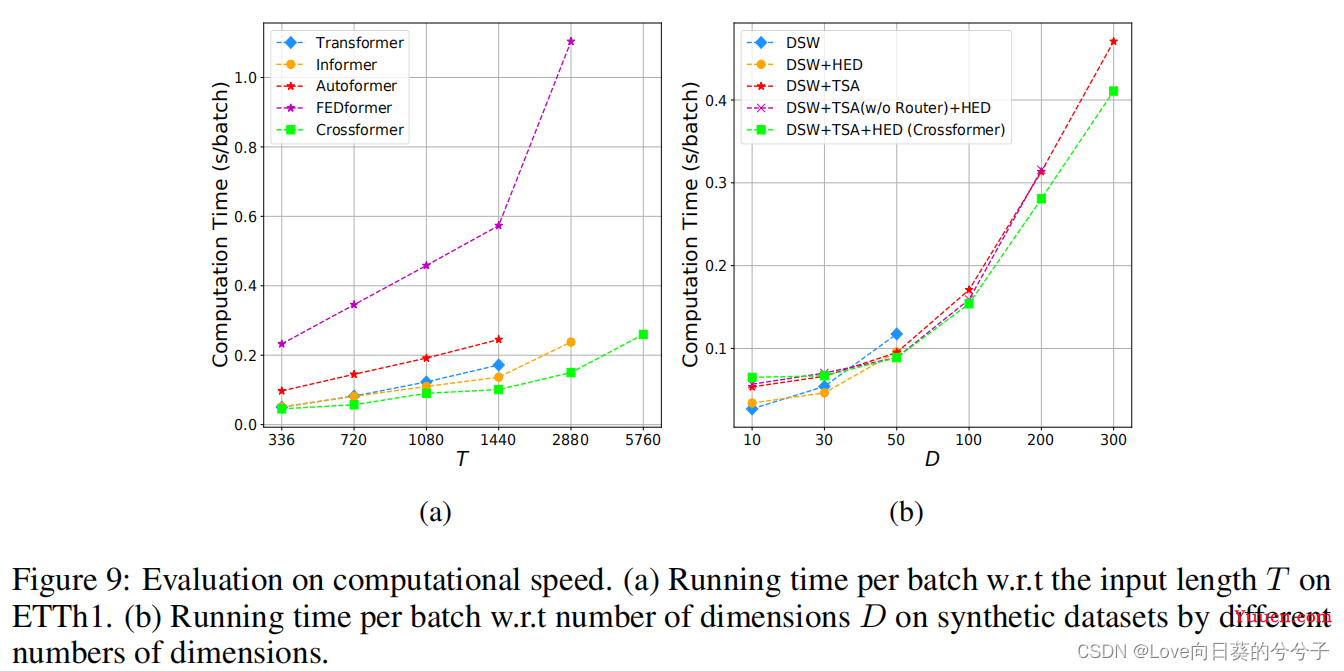
• 运行速度对比
  

5. 结论

• 提出了Crossformer，一种基于transformer的模型，利用跨维度依赖进行多元时间序列(MTS)预测。
• DSW (dimension - segment - wise)嵌入：将输入数据嵌入到二维矢量数组中，以保留时间和维度信息。
• 为了捕获嵌入式阵列的跨时间和跨维度依赖关系，设计两阶段注意(TSA)层。
• 利用DSW嵌入和TSA层，设计了一种分层编码器(HED)来利用不同尺度的信息。

在6个数据集上的实验结果展示了该方法优于之前的先进技术。

以上仅为本人小记，有问题欢迎指出(●ˇ∀ˇ●)