之前给大家写过一个临床预测模型：R数据分析：跟随top期刊手把手教你做一个临床预测模型，里面其实都是比较基础的模型判别能力discrimination的一些指标，那么今天就再进一步，给大家分享一些和临床决策实际相关的指标，主要是校准calibration和决策曲线Decision curve analysis。

校准曲线

做预测模型都应该报告校准曲线的：

Reporting on calibration performance is recommended by the TRIPOD (Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis) guidelines for prediction modeling studies

先给大家解释，预测模型为什么除了需要discrimination的一些指标外（比如tp,tn,fp,fn,roc，LR+,LR-等等）还需要做校准曲线：

Clinical predictive model performance is commonly published based on discrimination measures, but use of models for individualized predictions requires adequate model calibration

是因为：这些指标仅仅针对现有样本，很容易在过拟合的情况下，表现得很好。那么这种预测模型有没有用，敢不敢用？得打个问号。

in contrast to discrimination, which refers to the ability of a model to rank patients according to risk, calibration refers to the agreement between the estimated and the “true” risk of an outcome

依然是给大家举例子说明：一个区分度很好的预测模型，AUC很高，这个模型是以美国某个社区样本做的预测痴呆的模型，现在有人用这个模型预测全体社区老年人，发现按照模型的预测结果，美国将会有40%的老年人得痴呆，但是普查结果告诉我们美国痴呆患病率只有10%。这个就是一个过拟合的模型高估结局风险的例子（但这并不妨碍其在训练样本中表现的很好），但是这个模型不能用。

When predictive models are built based on a population that differs from the population in which they will be used, blind application of these models could result in large “residuals” (ie, a large difference between a model’s estimate and the true outcome) because of factors that are difficult to account for.

如何表示模型的上面的情况（预测值与实际值偏离）的严重程度，或者说如何评价模型能不能用，能不能换个样本也预测得准，就要评估模型的校准度，所以我们需要报告模型的校准曲线。

矫正曲线要做的就是对比模型预测概率和观测概率的一致性。因为我们是凭模型的预测概率判断具体病人阴阳性的，如果我的模型表现好，比如我依照0.5的预测概率划分阴阳，如果模型表现好，是不是应该100个预测概率是0.5的人会有50阳性？再来一个例子，比如我依照0.3的预测概率划分阴阳，如果模型表现好，是不是应该100个预测概率是0.3的人会有30阳性？

就是如果我的模型的校准度好，是不是就不会发生我刚刚据的痴呆预测的例子了，所以说：

Calibration plot is a visual tool to assess the agreement between predictions and observations in different percentiles (mostly deciles) of the predicted values.

校准曲线可以说明模型表现的另一个方面：Performance can further be quantified in terms of calibration (do close to x of 100 patients with a risk prediction of x% have the outcome?)

上面就是模型的矫正曲线来评估模型表现的理由，我们理想的情况就是我们的预测模型预测出来的Y和数据真实的Y之间的距离越小越好，如果我们的结局变量是连续变量，那么距离就是预测的y值和实际y值的差，如果结局是二分类变量那么距离就是阳性概率p和实际p的差：

The distance between the predicted outcome and actual outcome is central to quantify overall model performance from a statistical modeler’s perspective 32. The distance is Y −Ŷ for continuous outcomes. For binary outcomes, with Y defined 0 – 1, Ŷ is equal to the predicted probability p, and for survival outcomes it is the predicted event probability at a given time (or as a function of time)

在坐标系中，如果我们将模型预测概率放在横轴，实际概率放在纵轴，一个完美的预测模型的矫正曲线应该是一个45°向上过0的直线（Ideal），意味着模型预测概率和实际概率完全吻合。但是我们在论文中看到的矫正曲线一般是下图样子的：

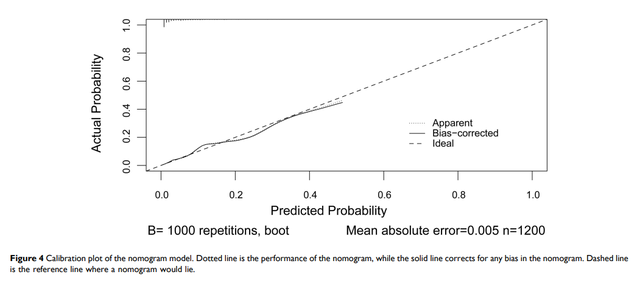
图中的Ideal线刚刚已经解释了（就是理想情况下模型预测和实际完全一致），图中还会有Apparent线和Bais-corrected线，这两个线就表示自己的模型的表现，Apparent线其中的意思是自己的训练的表现而Bais-corrected线表示样本经反复自助抽样后训练出的模型表现，其矫正了过拟合情况（另外一种理解：Apparent线为内部矫正，Bais-corrected线为模型的外部矫正曲线，外部数据怎么来的，自助抽样得来的）。此处不用纠结，发表的论文的中对矫正曲线的描述通常也就是一句话：

所以大家只要把握住，打眼一看，两条线都在Ideal线的周围没有偏离的太离谱就可以。

以上就是模型校准的基础知识，内容大部分参见文献：

Yingxiang Huang, Wentao Li, Fima Macheret, Rodney A Gabriel, Lucila Ohno-Machado, A tutorial on calibration measurements and calibration models for clinical prediction models, Journal of the American Medical Informatics Association, Volume 27, Issue 4, April 2020, Pages 621–633, https://doi.org/10.1093/jamia/ocz228

DCA曲线原理介绍

评价一种诊断方法是否好用，一般是作ROC曲线，计算AUC。但是，ROC只是从该方法的特异性和敏感性考虑，追求的是准确。而临床上我要用预测结果决定是不是需要采取干预，准确就足够了吗？准确度较高的情况下就一定要依照模型预测结果进行干预吗？干预后患者就一定受益吗？也得打个问号。

就是模型预测再准确，也不能百分百准确，始终有假阳性和假阴性存在，我们却要根据模型的预测结果去干预病人，这里面就有一个干预划不划得来的问题：说的再具体点，比如我通过某个生物标志物预测患者是否患了某病，无论选取哪个值为临界值，都会遇到假阳性的可能，假阳性的病人也会接受干预（但其实是亏损的），我们希望自己做出来的预测模型在临床使用中，在任何时候依照模型结果进行干预净受益都比默认的好（最常见的默认情况就是全干预和全不干预）。

那么决策曲线要干的事情是啥？就是将依照模型干预的净受益和默认方法（全干预和不干预）干预的净受益进行比较：

In brief, decision curve analysis calculates a clinical “net benefit” for one or more prediction models or diagnostic tests in comparison to default strategies of treating all or no patients.

有点抽象哈，什么是净受益？

用干预来举例，在预测模型中，我们在全干预的情况下（全部人群无差别干预），我们使用这种策略时真的受益应该是true positives和false negatives，我们的代价就是false positives和true negatives，此时受益减去代价就叫做净受益：

In the case of diagnosis, the income is true positives (e.g., finding a cancer) and the expenditure is false positives (e.g., unnecessary biopsies), with the “exchange rate” being the number of false positives that are worth one true positive. The exchange rate will depend on the relative seriousness of the intervention and outcome. For instance, we will be willing to conduct more unnecessary biopsies to find one cancer if the biopsy procedure is safe vs. dangerous or the cancer is aggressive vs. more indolent. The exchange rate is calculated, as explained above, from the threshold probability. Another analogy is with net health benefit or net monetary benefit, which both depend on the willingness to pay threshold in their exchange of benefits in terms of health and costs

其实上面的描述还是不严谨，临床决策考虑是不是施加干预，肯定还要考虑干预本身的危害性，比如如果干预完全是对病人无害的，那么想都不用想，管它三七二十一，就算病人只有0.1的概率患病，我也要把干预直接搞起来，因为干预没损害的嘛。

但是干预存在副作用的时候，我们可以有这么一个换算关系：多少个真阳性的干预获益能抵得上一个假阳性的干预损失？

回到我们的实际情形：如果现在模型告诉我，病人患病的概率是100%，我一定会给病人施加干预，毫无疑问！如果模型告诉我病人患病的概率是98%，我估摸着也给个干预看看（尽管这个干预有一定危害），那么如果模型告诉我病人患病的概率是90%，干预还是不干预呢？这个时候我就不知道了，有点懵。

有人说还是应该干预，那么请继续往下读：

但是过往的经验告诉我（或者我本身就知道）：一个副作用很强的干预，对于阳性病人干预的获益是对阴性病人干预损失的1/9（干预错的损失是干预一个真阳性获益的9倍），另一种理解就是我干预阳性病人9个人的获益和干预了1个阴性病人的损失可以抵消。此时如果模型告诉你，某病人阳性的概率是90%，请问你对不对它进行干预？

回答我！

聪明的你估计又想了想，好像这个时候不干预也行，因为这种时候干预在理论上其实是没有受益的（尽管模型告诉我它的病的概率达到90%，0.9*1/9=（1-0.9）*1）。

上面的‘阳性的概率是90%’中的90%就叫做阈概率（Threshold Probability），表示的是只有病人的预测概率超过这个阈概率，干预才有受益，才值得干预：

threshold probabilities, defined as the minimum probability of disease at which further intervention would be warranted, as net benefit = sensitivity × prevalence – (1 – specificity) × (1 – prevalence) × w where w is the odds at the threshold probability

这个阈概率本身我们是不知道的，但是我们关心的是是不是我们的训练出来的模型在任何阈概率情况下都是有收益的，都是值得应用的，这就是DCA曲线要帮助我们回答的问题。

所以请大家记住：决策曲线要描述的对象是整个预测模型或者是某个测验，就是要看按照模型结果进行干预的净受益。

我们还是再看一眼DCA曲线：

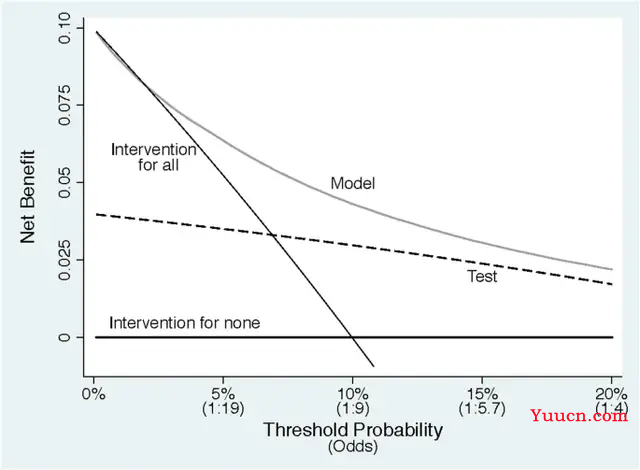
DCA曲线的横轴是阈概率，纵轴是净获益，可以看到阈概率在DCA曲线上展示的都是比较小的，刚刚给大家举的例子着实有点极端了。再回顾一下净获益，刚刚写了获益的意思是正确识别阳性，但是模型其实还有损失的嘛（就是错误的识别了阳性），因为对于阳性我们就得进行干预，但是干预有没有益处，得比较两个东西------就是真阳性的获益和假阳性的损失，两个做差就叫做净获益。

这样DCA曲线就可以描述随着阈概率变化，按照模型预测值进行干预的情况下净获益的变化。

注意曲线中有一条叫做“intervention for all”，就是极端情况，所有人都进行干预，这个时候只有真阳性才获益，如果阈概率从小到大变化（就是干预错的损失/干预的获益的值从小到大变化，比如看图中横轴的1：19到1：9）那么所有人都进行干预整体净获益肯定会从大到小变，就是随着阈概率的增大（干预的损失增大/干预获益的比值的增大）那么对所有人都进行干预的净获益也会逐渐减小（这就是为什么intervention for all的斜率是负的）。

注意曲线中有一条叫做“intervention for none”,就是极端情况，所有人都不进行干预，这个时候无论阈概率如何变化净获益肯定为0，很好理解，因为你都不干预嘛，哪里有干预获益的道理？。所以这条线一直是平的。

“intervention for all”这条线和“intervention for none”这条线还有一个交点，就是说在某个阈概率水平下，对于阳性病人采取全干预和全不干预的净获益都是一样的，就像刚刚给大家写的例子反过来：如果干预一个真阳性病人的获益是9，干预一个假阳性病人的损失是1，此时阈概率应该为1/（9+1）=0.1，就是说在这种情况下阈概率为0.1的时候两条线就会相交。

在换个思维再给大家举个例子，现在假设我知道我预测的人群的某病患病率为0.2，某干预方法的干预真阳性的受益是8，干预假阳性的损失是2，那么此时对应的阈概率为2/（2+8）=0.2，此时采用全干预策略的净获益为0.2*8-2*0.8=0，此时两条线相交。

通过上面两个例子，应该大家就可以理解了：在阈概率等于研究人群患病率的这个点，两条线会相交，也就是全干预策略的净受益为0。

上面的部分行文思路来源于文献，感兴趣的同学建议还是去阅读原文哦：

Vickers, A.J., van Calster, B. & Steyerberg, E.W. A simple, step-by-step guide to interpreting decision curve analysis. Diagn Progn Res 3, 18 (2019). https://doi.org/10.1186/s41512-019-0064-7

如何读DCA曲线

再回到下图就是一个DCA曲线的常见样子，不过这个曲线将预测模型和另外一个检测技术test，画在了一个图上，那么怎么读图呢？

首先图中两条实线是两个最极端的情况，一个叫做“intervention for all”，另一个叫做"intervention for none"，刚刚解释过它们的意思了。

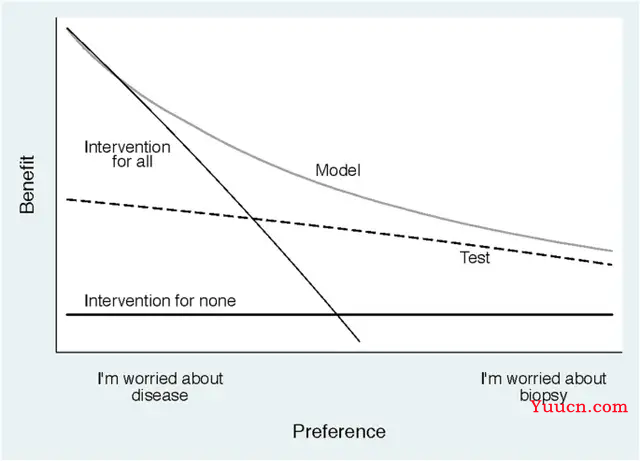
可以从图中看出，随着阈概率的增加，模型的净受益会下降（更精确的说法是根据模型结果进行干预的净受益会下降），但是对于我们训练的Model来讲，按照Model的预测结果进行干预的话，除了阈概率很小的情况下，在其余的阈概率情形下模型的表现都是比较好的，并且模型表现始终比test好。

做好预测模型之后，咱们把这个图给亮出来，就相当于给编辑说明了我做的这个预测模型确实好，确实比现有的检测技术管用，赶紧发表出来吧，这个就是DCA曲线。

Hence, we can conclude that, except for a small range of low preferences, intervening on (i.e., biopsying) patients on the basis of the prediction model leads to higher benefit than the alternative strategies of biopsying all patients, biopsying no patients, or only biopsy those patients who are positive on the diagnostic test. For the prostate biopsy study, the conclusion is that using the model to determine whether patients should have a biopsy would lead to improved clinical outcome.

小结

今天给大家介绍了临床预测模型中矫正曲线和决策曲线的意义（仅以2分类结局为例），本来想的是将做法一起写的，无奈写的太罗嗦，字符限制了，那就分为2期吧，下期就出实操，希望对大家有启发。