系列文章目录

一、Python二手房价格预测（一）——数据获取

二、Python二手房价格预测（二）——数据处理及数据可视化

前言

        在上次分享中我们对数据进行了部分预处理和数据可视化，接下来将对数据完全处理，并且使用几种基线模型对二手房的价格进行预测。

一、数据处理

        上次分享中我们将部分数据处理成了数值型数据，还有部分Object类型数据没有进行处理，先对这些数据进行一个处理。

def xiaoquInfo(df, flag):
    xiaoqu = json.loads(df['小区简介'].replace("'", '"'))
    if flag == 1:
        return int(xiaoqu['小区建造年份'][:-1])
    elif flag == 2:
        return int(xiaoqu['楼栋总数'][:-1])
    else:
        return xiaoqu['小区均价']
data['小区建造年份'] = data.apply(lambda x:xiaoquInfo(x, 1), axis=1)
data['楼栋总数'] = data.apply(lambda x:xiaoquInfo(x, 2), axis=1)
data['小区均价'] = data.apply(lambda x:xiaoquInfo(x, 3), axis=1)
# 剔除一些无用列，其中“户型分间”列还可以提取一些东西，这里为了节约时间我就没做，有能力的同学可以试着提取一些有效数据
data = data[['总价', '单位价格', '楼房信息', '所属区县', '所在楼层', '建筑面积', '户型结构', '套内面积', '建筑类型', '房屋朝向', '建筑结构', '装修情况', '供暖方式', '配备电梯', '挂牌时间', '交易权属', '上次交易', '房屋用途', '房屋年限', '产权所属', '抵押信息', '房屋户型_室', '房屋户型_厅', '房屋户型_厨', '房屋户型_卫', '梯户比例_梯', '梯户比例_户', '梯户比例_比例', '小区建造年份', '楼栋总数', '小区均价']]
# 将列中只含两种类型的列进行0-1转换，“抵押信息”列中，可以理解为只含“无抵押”和“有抵押”
def diyaInfo(df):
    if df['抵押信息'] == '无抵押':
        return 0
    else:
        return 1
data['抵押信息_01'] = data.apply(lambda x:diyaInfo(x), axis=1)
data['产权所属'] = data['产权所属'].replace("非共有", 0).replace("共有", 1)
# 将数据获取时间定义
data['数据获取日期'] = '2022-04-24'
# 定义一下处理日期型数据的函数，将日期转化为时间差值，天为单位
import datetime
def calDate(df, c):
    if df[c] == '暂无数据':
        return np.nan
    d1=datetime.datetime.strptime('2022-04-24',"%Y-%m-%d")
    d2=datetime.datetime.strptime(df[c],"%Y-%m-%d")
    diff_days=d1-d2
    return diff_days.days
for c in ['挂牌时间', '上次交易']:
    data[c+'差（天）'] = data.apply(lambda x:calDate(x, c), axis=1)
# 有空缺值按均值填充了
for c in ['挂牌时间差（天）', '上次交易差（天）']:
    data[c].fillna(data[c].mean(), inplace=True)
# 生成房龄数据
data['房龄'] = 2022 - data['楼房信息']
# 将某些列做独热编码处理，房屋朝向这一列含有的类别过多，做独热编码时会使数据稀疏，因此，将一些少量类别的数据进行合并为“其他朝向”
def calChaoxiang(df):
    chaoxiangCol = ['南 北', '南', '东南', '西南', '北 南', '东 南 北', '西北', '西', '东', '南 西 北', '东北', '北', '东 西', '南 北 西', '东 北', '南 北 东']
    if df['房屋朝向'] not in chaoxiangCol:
        return "其他朝向"
    else:
        return df['房屋朝向']
data['房屋朝向'] = data.apply(lambda x:calChaoxiang(x), axis=1)
one_hot_col_names = ['所属区县',
 '所在楼层',
 '户型结构',
 '建筑类型',
 '房屋朝向',
 '建筑结构',
 '装修情况',
 '供暖方式',
 '配备电梯',
 '交易权属',
 '房屋用途',
 '房屋年限']
# 删除已处理过的时间列
data.drop(['挂牌时间', '上次交易', '数据获取日期'], axis=1, inplace=True)
one_hot_data = pd.get_dummies(data[one_hot_col_names])
data = pd.concat([data,one_hot_data],axis = 1)
data.drop(one_hot_col_names, axis=1, inplace=True)
# 将处理过的数据导出（注意，这一部分代码要续上之前分享过的代码，上次数据处理不完全）
data.to_excel("二手房数据（处理后）.xlsx", index=False)

二、模型训练

1.引入库

代码如下：

# 写在前面，大家可以关注一下微信公众号：吉吉的机器学习乐园
# 可以通过后台获取数据，不定期分享Python，Java、机器学习等相关内容
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator
import sys
import seaborn as sns
import warnings
import math
warnings.filterwarnings("ignore")
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
pd.set_option('display.max_rows', 100,'display.max_columns', 1000,"display.max_colwidth",1000,'display.width',1000)
from sklearn.metrics import *
from sklearn.linear_model import *
from sklearn.neighbors import *
from sklearn.svm import *
from sklearn.neural_network import *
from sklearn.tree import *
from sklearn.ensemble import *
from xgboost import *
import lightgbm as lgb
import tensorflow as tf
from tensorflow.keras import layers
from sklearn.preprocessing import *
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.model_selection import *

2.读入数据

代码如下：

data = pd.read_excel("二手房数据（处理后）.xlsx", na_values=np.nan)
# 将数据划分输入和结果集
X = data[ data.columns[1:] ]
y_reg = data[ data.columns[0] ]
# 切分训练集和测试集， random_state是切分数据集的随机种子，要想复现本文的结果，随机种子应该一致
x_train, x_test, y_train, y_test = train_test_split(X, y_reg, test_size=0.3, random_state=42)

3.评价指标

1. 平均绝对误差（MAE）

        平均绝对误差的英文全称为 Mean Absolute Error，也称之为 L1 范数损失。是通过计算预测值和真实值之间的距离的绝对值的均值，来衡量预测值与真实值之间的距离。计算公式如下：

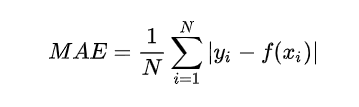
2. 均方误差（MSE）

        均方误差英文全称为 Mean Squared Error，也称之为 L2 范数损失。通过计算真实值与预测值的差值的平方和的均值来衡量距离。计算公式如下：

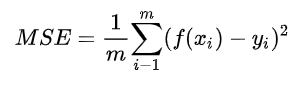
3. 均方根误差（RMSE）

        均方根误差的英文全称为 Root Mean Squared Error，代表的是预测值与真实值差值的样本标准差。计算公式如下：

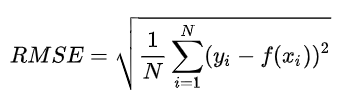
4. 决定系数（R2）

        决定系数评估的是预测模型相对于基准模型（真实值的平均值作为预测值）的好坏程度。计算公式如下：

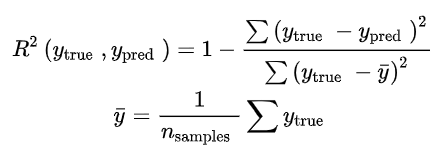
• 最好的模型预测的 R2 的值为 1，表示预测值与真实值之间是没有偏差的；

• 但是最差的模型，得到的 R2 的值并不是 0，而是会得到负值；

• 当模型的 R2 值为负值，表示模型预测结果比基准模型（均值模型）表现要差；

• 当模型的 R2 值大于 0，表示模型的预测结果比使用均值预测得到的结果要好。

定义评价指标函数：

# 评价指标函数定义，其中R2的指标可以由模型自身得出，后面的score即为R2
def evaluation(model):
    ypred = model.predict(x_test)
    mae = mean_absolute_error(y_test, ypred)
    mse = mean_squared_error(y_test, ypred)
    rmse = math.sqrt(mse)
    print("MAE: %.2f" % mae)
    print("MSE: %.2f" % mse)
    print("RMSE: %.2f" % rmse)
    return ypred

4.线性回归

代码如下：

model_LR = LinearRegression()
model_LR.fit(x_train, y_train)
print("params: ", model_LR.get_params())
print("train score: ", model_LR.score(x_train, y_train))
print("test score: ", model_LR.score(x_test, y_test))
predict_y = evaluation(model_LR)

输出结果：

params:  {'copy_X': True, 'fit_intercept': True, 'n_jobs': None, 'normalize': False}
train score:  0.9393799595620992
test score:  0.9369392050137573
MAE: 12.11
MSE: 370.69
RMSE: 19.25

我们可以将 y_test 转换为 numpy 的 array 形式，方便后面的绘图。

test_y = np.array(y_test)

由于数据量较多，我们取预测结果和真实结果的前50个数据进行绘图。

plt.figure(figsize=(10,10))
plt.title('线性回归-真实值预测值对比')
plt.plot(predict_y[:50], 'ro-', label='预测值')
plt.plot(test_y[:50], 'go-', label='真实值')
plt.legend()
plt.show()

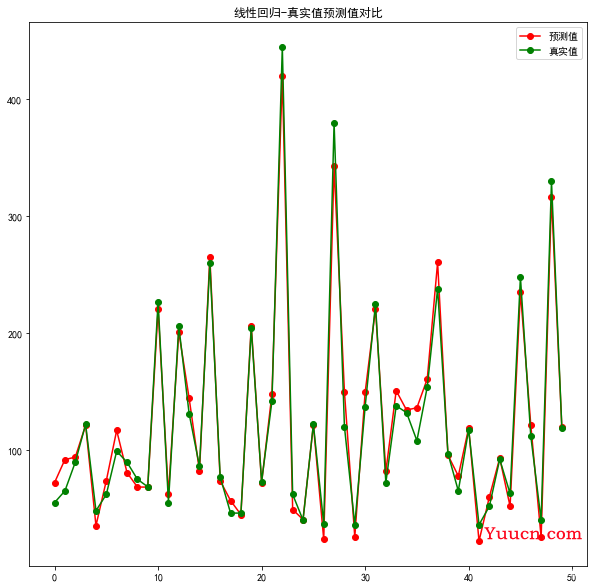
上图中，绿色点为真实值，红色点为预测值，当两点几乎重合时，说明模型的预测结果十分接近。

5.K近邻

代码如下：

model_knn = KNeighborsRegressor()
model_knn.fit(x_train, y_train)
print("params: ", model_knn.get_params())
print("train score: ", model_knn.score(x_train, y_train))
print("test score: ", model_knn.score(x_test, y_test))
predict_y = evaluation(model_knn)

输出结果：

params:  {'algorithm': 'auto', 'leaf_size': 30, 'metric': 'minkowski', 'metric_params': None, 'n_jobs': None, 'n_neighbors': 5, 'p': 2, 'weights': 'uniform'}
train score:  0.8055745690649098
test score:  0.7144393809856229
MAE: 27.67
MSE: 1678.59
RMSE: 40.97

绘图：

plt.figure(figsize=(10,10))
plt.title('KNN-真实值预测值对比')
plt.plot(predict_y[:50], 'ro-', label='预测值')
plt.plot(test_y[:50], 'go-', label='真实值')
plt.legend()
plt.show()

6.决策树回归

代码如下：

model_dtr = DecisionTreeRegressor(max_depth = 5, random_state=30)
model_dtr.fit(x_train, y_train)
print("params: ", model_dtr.get_params())
print("train score: ", model_dtr.score(x_train, y_train))
print("test score: ", model_dtr.score(x_test, y_test))
predict_y = evaluation(model_dtr)

        在这里，决策树学习器加入了一个 max_depth 的参数，这个参数限定了树的最大深度，设置这个参数的主要原因是为了防止模型过拟合

输出结果：

params:  {'criterion': 'mse', 'max_depth': 5, 'max_features': None, 'max_leaf_nodes': None, 'min_impurity_decrease': 0.0, 'min_impurity_split': None, 'min_samples_leaf': 1, 'min_samples_split': 2, 'min_weight_fraction_leaf': 0.0, 'presort': False, 'random_state': 30, 'splitter': 'best'}
train score:  0.9624891829996234
test score:  0.9457849042838976
MAE: 12.19
MSE: 318.69
RMSE: 17.85

如果不限定树的最大深度会发生什么呢？

model_dtr = DecisionTreeRegressor(random_state=30)
model_dtr.fit(x_train, y_train)
print("params: ", model_dtr.get_params())
print("train score: ", model_dtr.score(x_train, y_train))
print("test score: ", model_dtr.score(x_test, y_test))
predict_y = evaluation(model_dtr)

输出结果：

params:  {'criterion': 'mse', 'max_depth': None, 'max_features': None, 'max_leaf_nodes': None, 'min_impurity_decrease': 0.0, 'min_impurity_split': None, 'min_samples_leaf': 1, 'min_samples_split': 2, 'min_weight_fraction_leaf': 0.0, 'presort': False, 'random_state': 30, 'splitter': 'best'}
train score:  1.0
test score:  0.9819886071850025
MAE: 4.36
MSE: 105.88
RMSE: 10.29

获得树的最大深度：

model_dtr.get_depth()

输出结果：

17

        我们发现，在不限定树的最大深度时，决策树模型的训练得分（R2）为：1.0，但测试得分为：0.9819886071850025。
        这就是模型过拟合，在训练数据上的表现非常良好，当用未训练过的测试数据进行预测时，模型的泛化能力不足，导致测试结果不理想。
        感兴趣的同学可以自行查阅关于决策树剪枝的过程。

绘图：

plt.figure(figsize=(10,10))
plt.title('决策树回归-真实值预测值对比')
plt.plot(predict_y[:50], 'ro-', label='预测值')
plt.plot(test_y[:50], 'go-', label='真实值')
plt.legend()
plt.show()

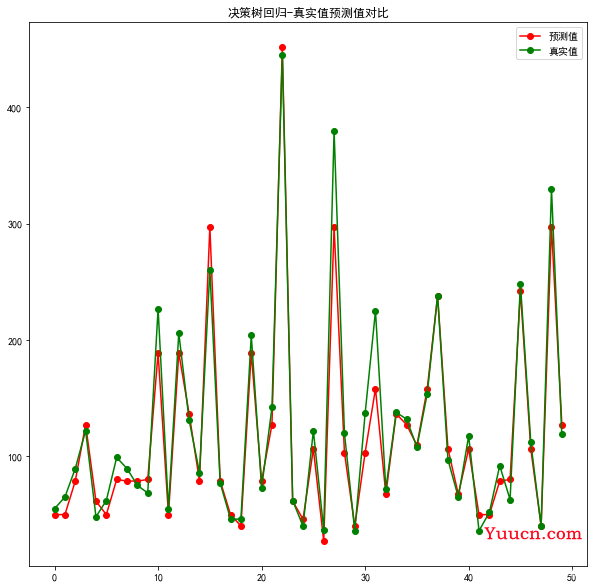
7.随机森林

代码如下：

model_rfr = RandomForestRegressor(random_state=30)
model_rfr.fit(x_train, y_train)
print("params: ", model_rfr.get_params())
print("train score: ", model_rfr.score(x_train, y_train))
print("test score: ", model_rfr.score(x_test, y_test))
predict_y = evaluation(model_rfr)

输出结果：

params:  {'bootstrap': True, 'criterion': 'mse', 'max_depth': None, 'max_features': 'auto', 'max_leaf_nodes': None, 'min_impurity_decrease': 0.0, 'min_impurity_split': None, 'min_samples_leaf': 1, 'min_samples_split': 2, 'min_weight_fraction_leaf': 0.0, 'n_estimators': 10, 'n_jobs': None, 'oob_score': False, 'random_state': 30, 'verbose': 0, 'warm_start': False}
train score:  0.9950702190060036
test score:  0.9891553887607397
MAE: 3.07
MSE: 63.75
RMSE: 7.98

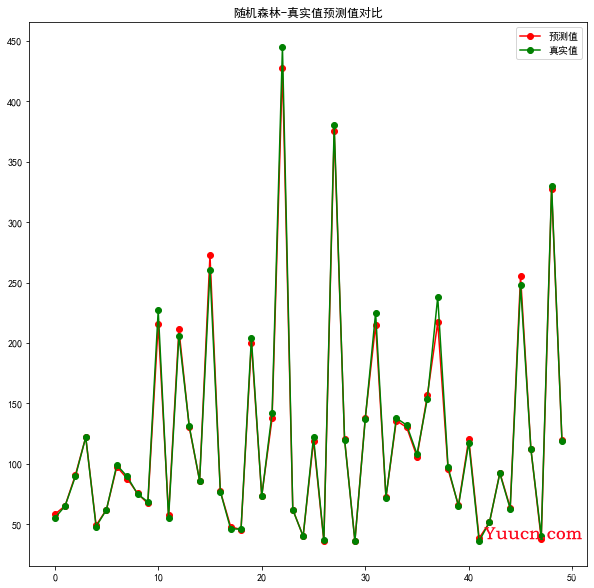
绘图：

plt.figure(figsize=(10,10))
plt.title('随机森林-真实值预测值对比')
plt.plot(predict_y[:50], 'ro-', label='预测值')
plt.plot(test_y[:50], 'go-', label='真实值')
plt.legend()
plt.show()

8.各模型结果

重新定义一个评估函数

def evaluation2(model):
    ypred = model.predict(x_test)
    mae = mean_absolute_error(y_test, ypred)
    mse = mean_squared_error(y_test, ypred)
    rmse = math.sqrt(mse)
    return ypred, mae, mse, rmse
# 记录各个模型的误差及R2得分
maeList = []
mseList = []
rmseList = []
trainr2List = []
testr2List = []
for model in [model_LR, model_knn , model_dtr, model_rfr]:
    ypred, mae, mse, rmse = evaluation2(model)
    trainr2 = model.score(x_train, y_train)
    testr2 = model.score(x_test, y_test)
    maeList.append(mae)
    mseList.append(mse)
    rmseList.append(rmse)
    trainr2List.append(trainr2)
    testr2List.append(testr2)
# 用折线图可视化一下
plt.figure(figsize=(8,6))
# plt.subplot(1,3,1)
plt.plot(['线性回归', 'KNN', '决策树', '随机森林'], maeList, '--^', label="MAE")
plt.plot(['线性回归', 'KNN', '决策树', '随机森林'], rmseList, '--*', label="RMSE")
plt.legend()
plt.show()
plt.figure(figsize=(8,6))
# plt.subplot(1,3,2)
plt.plot(['线性回归', 'KNN', '决策树', '随机森林'], mseList, '--o', label="MAE")
plt.legend()
plt.show()
plt.figure(figsize=(8,6))
# plt.subplot(1,3,3)
plt.plot(['线性回归', 'KNN', '决策树', '随机森林'], trainr2List, '--x', label="Train R2")
plt.plot(['线性回归', 'KNN', '决策树', '随机森林'], testr2List, '--v', label="Test R2")
plt.legend()
plt.show()

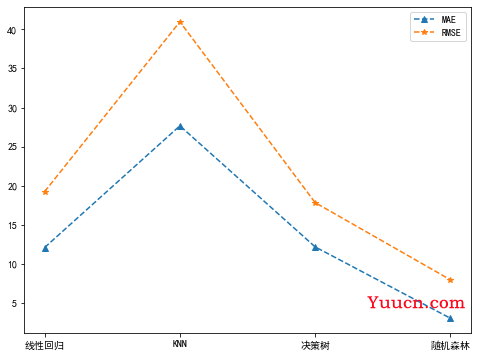
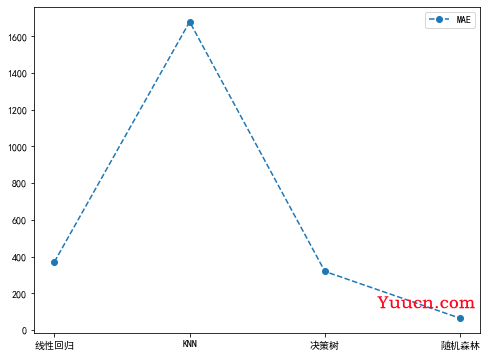
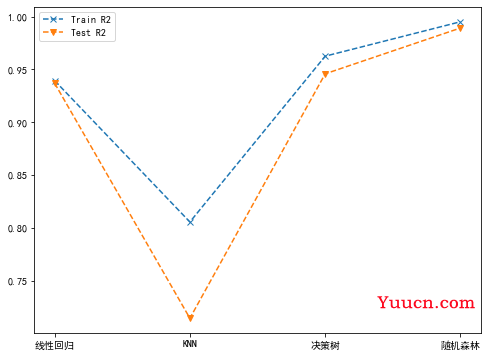
        从上面的图中可以看出，随机森林模型的整体表现最好（随机森林yyds）。当然，这不代表最优结果，因为上述几种模型都没有进行调参优化，经过调参后的各个模型效果还有可能提升。

三、重要特征筛选

        为了提升模型效果也可以对数据做特征筛选，这里可以通过相关系数分析法，将影响二手房售价的特征与售价做相关系数计算，pandas包很方便的集成了算法，并且可以通过seaborn、matplotlib等绘图包将相关系数用热力图的方式可视化。

# 这里的列取data中，除0-1和独热编码形式的数据
corr_cols = list(data.columns[:20])
test_data = data[corr_cols]
test_data_corr = test_data.corr()
price_corr = dict(test_data_corr.iloc[0])
price_corr = sorted(price_corr.items(), key=lambda x: abs(x[1]), reverse=True)
# 输出按绝对值排序后的相关系数
price_corr

输出结果，除"总价"外，共有19个特征：

[('总价', 1.0),
 ('单位价格', 0.8222981290702119),
 ('小区均价', 0.7687546742386121),
 ('建筑面积', 0.7251709920087407),
 ('套内面积', 0.7204559353359032),
 ('房屋户型_卫', 0.6312862646749),
 ('房屋户型_室', 0.5902144343661491),
 ('房屋户型_厅', 0.39760899920810316),
 ('梯户比例_比例', -0.3133978158118177),
 ('小区建造年份', 0.2796377353906572),
 ('梯户比例_户', -0.27384128491689264),
 ('房龄', -0.22880814058196702),
 ('楼房信息', 0.2288081405819666),
 ('上次交易差（天）', -0.1499606404095348),
 ('抵押信息_01', 0.0854414739678885),
 ('挂牌时间差（天）', 0.07980048870698007),
 ('梯户比例_梯', -0.06639533403491238),
 ('产权所属', 0.05344184918071662),
 ('房屋户型_厨', 0.04939490040354267),
 ('楼栋总数', -0.04560798084636813)]

绘制热力图：

price_corr_cols = [ r[0] for r in price_corr ]
price_data = test_data_corr[price_corr_cols].loc[price_corr_cols]
plt.figure(figsize=(15, 10))
plt.title("相关系数热力图")
ax = sns.heatmap(price_data, linewidths=0.5, cmap='OrRd', cbar=True)
plt.show()

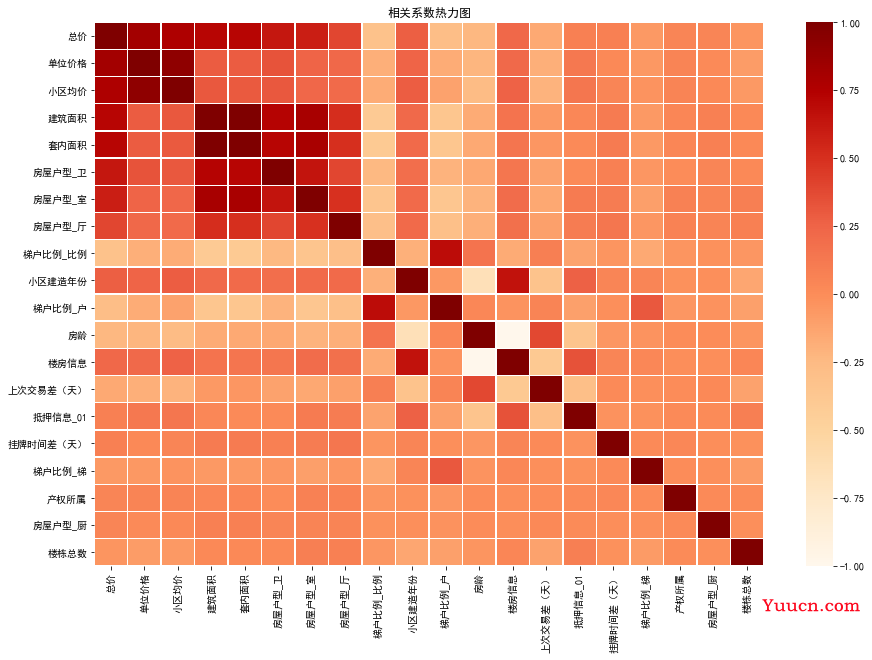
        为了验证相关系数分析出来的重要特征是否对模型有效，我们将模型效果最好的随机森林模型的前19个重要特征输出。

feature_important = sorted(
    zip(x_train.columns, map(lambda x:round(x,4), model_rfr.feature_importances_)),
    key=lambda x: x[1],reverse=True)
for i in range(19):
    print(feature_important[i])

输出结果：

('单位价格', 0.6123)
('建筑面积', 0.2775)
('套内面积', 0.0853)
('小区均价', 0.0121)
('挂牌时间差（天）', 0.0025)
('所属区县_和平', 0.0022)
('房屋户型_卫', 0.001)
('楼栋总数', 0.001)
('楼房信息', 0.0008)
('梯户比例_梯', 0.0008)
('小区建造年份', 0.0006)
('房龄', 0.0006)
('上次交易差（天）', 0.0005)
('户型结构_暂无数据', 0.0004)
('房屋户型_室', 0.0002)
('梯户比例_比例', 0.0002)
('抵押信息_01', 0.0002)
('配备电梯_有', 0.0002)
('房屋用途_别墅', 0.0002)

        将相关系数分析出来的重要特征集合与随机森林的前19个重要特征取交集，并输出有多少个重复的特征。

f1_list = []
f2_list = []
for i in range(19):
    f1_list.append(feature_important[i][0])
for i in range(1, 20):
    f2_list.append(price_corr[i][0])
cnt = 0
for i in range(19):
    if f1_list[i] in f2_list:
        print(f1_list[i])
        cnt += 1
print("共有"+str(cnt)+"个重复特征！")

输出结果：

单位价格
建筑面积
套内面积
小区均价
挂牌时间差（天）
房屋户型_卫
楼栋总数
楼房信息
梯户比例_梯
小区建造年份
房龄
上次交易差（天）
房屋户型_室
梯户比例_比例
抵押信息_01
共有15个重复特征！

结语

        回归预测模型的baseline总是相似的，掌握好套路就可以轻松得到一个baseline结果，一般都是先将数据进行清洗，将非数值型数据通过一些规则转化成数值型数据，再进行多特征的模型训练，一通百通。希望能给大家抛砖引玉，同学们可以根据自己的需求处理数据，不同的处理方法，模型的效果可能也不相同。回归问题的预测写了有两个系列的博客了，接下来应该不会再更新这方面的内容了，尝试一些新的知识，比如NLP、图像识别、推荐系统等等。我喜欢根据问题提出实际的解决方法，从0到1的去实现（掉包除外，hhh，有机会再从头好好学学原理，写各个模型的源码才有意思），因此可能就某些问题写一些实战。即将毕业，马上步入工作岗位了，希望能坚持下来写博客分享的习惯~