前言

随着我们了解到机器人如何建立运动学模型和动力学模型之后,我们可以使用Matlab中的仿真工具箱内来对模型的准确性进行验证,并且可以通过内置的函数进行简单的轨迹规划和可视化观察,本节涉及到的工具箱是MATLAB自带的Robotics Toolbox工具箱。
一、工具箱介绍及安装
1. 功能介绍
- Robotics Toolbox:MATLAB自带的工具箱,常用于实现有关于机械臂的仿真,包含齐次变换求解、正逆运动学求解、雅可比矩阵、动力学仿真以及轨迹规划等功能。
- 作用:由于高自由度机器人的运动学和动力学模型较为复杂,容易产生计算错误,通过使用相应的封装函数可以极大的提高计算效率,验证模型正确性,并通过MATLAB强大的可视化功能,对机器人的实际机理有更加清晰的认识。
- 常用函数:Link、SerialLink、display、fkine和Jtraj函数,分别对应机器人的连杆配置、机器人连接、可视化演示、运动学正解和给定位置的轨迹规划
2. 安装教程
-
下载工具箱文件夹:下载地址:Robotics Toolbox

-
解压文件并放置于指定文件夹
-
将该文件夹路径添加到MATALB路径中:
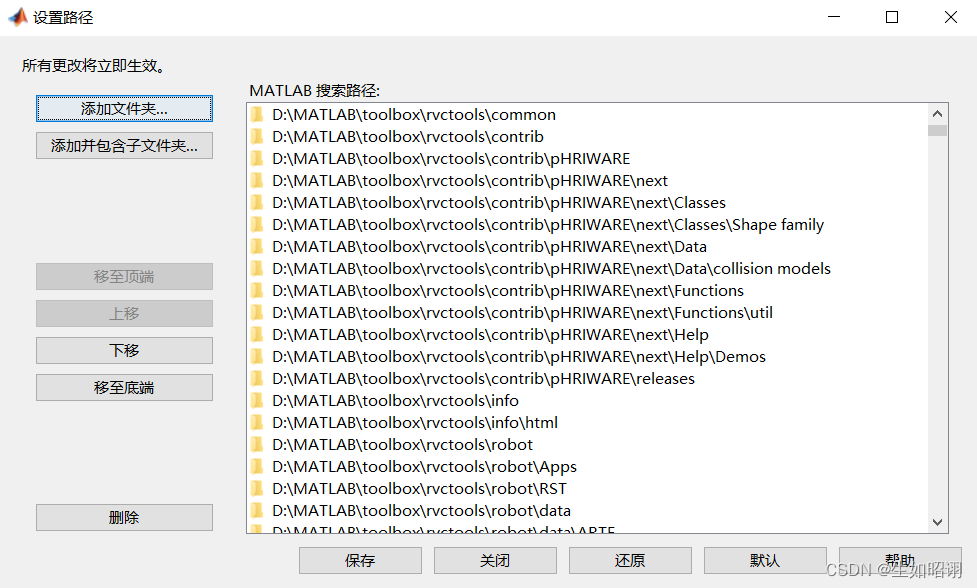
-
打开MATLAB命令行:窗口输入指令
startup_rvc
二、运动学常用函数
1. 设置机器人连杆:Link函数
1)参数介绍:
alpha A theta D sigma convention 关节扭角 连杆长度 关节角度 关节偏置 区分转动关节(0)和移动关节(1) 区分modified和standard两种DH模型
2)代码示例:
% 各连杆参数(虚拟)
l1= 0.08;
l2= 0.2;
l3= 0.2;
% 基本偏置参数
thetaVal = zeROS(4,1);
% 定义各个连杆以及关节类型,默认为转动关节
% theta d a alpha
% 连杆偏距d 连杆长度 关节偏角alpha
L1=Link([ 0 0 0 0], 'modified'); % [四个DH参数], options
L2=Link([ 0 0 l1 -pi/2], 'modified');
L3=Link([ 0 0 l2 0], 'modified');
L4=Link([ 0 ,0 l3 0], 'modified');
2. 连接连杆构成机械臂:SerialLink函数
1)参数介绍:
name offset 机器人名称 各连杆偏置参数
2)代码示例:
% 将连杆组成机械臂
robot=SerialLink([L1,L2,L3,L4]);
robot.name='singleLeg';
robot.offset=thetaVal;
3)输出窗口:

3. 3D演示与示教:display和teach函数
1)代码示例:
% 基本演示
robot.display();
view(3);
% 解决robot.teach()和plot的索引超出报错
robot.teach();
2)可视化界面:
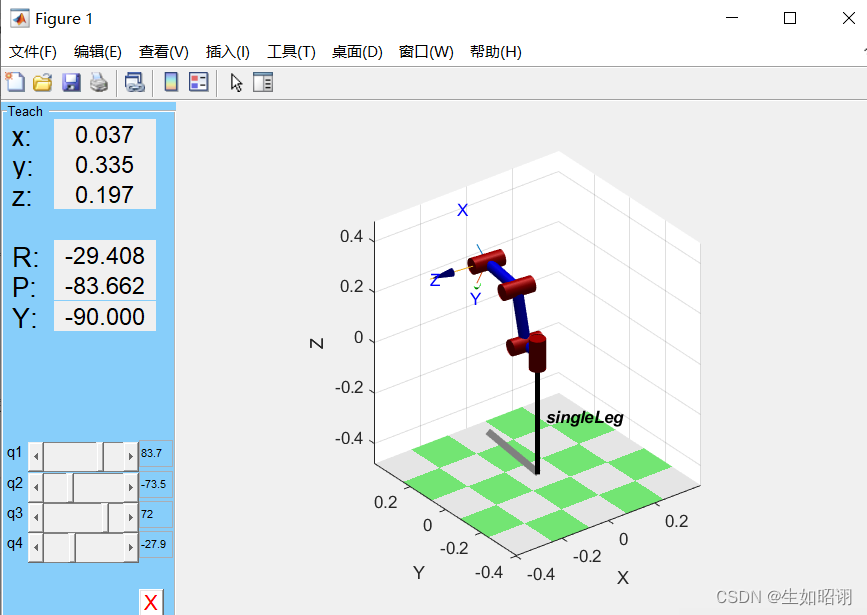
4. 正逆运动学求解:fkine和ikine函数
1)使用方法:
函数 输入 输出 备注 fkine 各关节变量值 齐次变换矩阵 默认弧度,输入为1*N矩阵 ikine 齐次变换矩阵、初始值 各关节变量值 默认计算6自由度以上的机械臂,需要mask通知
注:在实际过程中较少使用ikine函数,可自行编写运动学反解函数;
2)代码示例:
% 运动学正解验证
q1 = 30*pi/180;
q2 = 30*pi/180;
q3 = -60*pi/180;
qn = [q1 q2 q3 0];
T = robot.fkine(qn)
% 运动学逆解验证
% theta d a alpha sigma
L(1) = Link([ 0 0 10 0 0 ]);
L(2) = Link([ 0 0 20 0 0 ]);
% 正运动学解算,得到机器人末端的齐次变换矩阵
init = [0 pi/4];
targ = [pi/2 pi];
T0=robot.fkine(init);
TF=robot.fkine(targ);
% 得到机器人在变换过程中每一步(step)的齐次变换矩阵
step = 200;
TC=ctraj(T0,TF,step);
% 逆运动学计算
qq=robot.ikine(TC,'mask',[1 1 1 0 0 0]);
5. 轨迹规划:Jtraj函数
1)参数分析:
输入 始终点位姿、采样点个数 位姿:1*N弧度值 输出 各关节角度、角速度、角加速度 单位:弧度
2)代码示例:
% 五项式轨迹规划动态
% 设定位姿为(0.4,0.1,-0.1 -- 0.4,0.1,0.1)
%根据起始点位姿,得到起始点关节角
q1=[-14.036*pi/180 46.76*pi/180 -60*pi/180 0];
%根据终止点位姿,得到终止点关节角
q2=[-14.036*pi/180 13.24*pi/180 -60*pi/180 0];
%五次多项式轨迹,得到关节角度,角速度,角加速度,50为采样点个数
[q ,qd, qdd]=jtraj(q1,q2,50);
grid on
%根据插值,得到末端执行器位姿
T=robot.fkine(q);
nT=T.T;
plot3(squeeze(nT(1,4,:)),squeeze(nT(2,4,:)),squeeze(nT(3,4,:)));
6. 实时运动动画:plot函数
- 输入参数:关节角度和设置参数,下面简要介绍参数
名称 值 说明 实例 workplace W W为1×6的行向量,用来表示视野的xyz轴范围 w=[-20 20 -20 20 -20 20] floorlevel L 楼板的z坐标值(目前咱不了解) delay D 动画帧之间的延迟(单位:s),用这个可以用来控制动画中机器人动作的快慢 D=0.01 [no]loop 是否永远在轨道上循环 fps fps 每秒钟帧率,使用fps时候delay不起作用 fps=60 trail L 绘制机器人末端的轨迹,L的值表示轨迹颜色 L=‘r’ movie M 保存成动画到当前文件夹,M是文件名 M=‘test.gif’ scale S 关节大小的比例因子 S=0.5 view V V=[az el],通过方位角az和el来调整视角 L=[45,25]
robot.plot(q,'workspace',[-40 40 -40 40 -40 40],'delay',0.001,'fps',120,'trail','b','view',[30,50]);
% 注:在实际的简单操作中可以直接使用默认options,故只输入关节角度即可
2)代码示例:
[q ,qd, qdd]=jtraj(q1,q2,50);
grid on
%根据插值,得到末端执行器位姿
T=robot.fkine(q);
nT=T.T;
plot3(squeeze(nT(1,4,:)),squeeze(nT(2,4,:)),squeeze(nT(3,4,:)));
%输出末端轨迹
hold on
%动画演示
robot.plot(q);
3)动画界面:
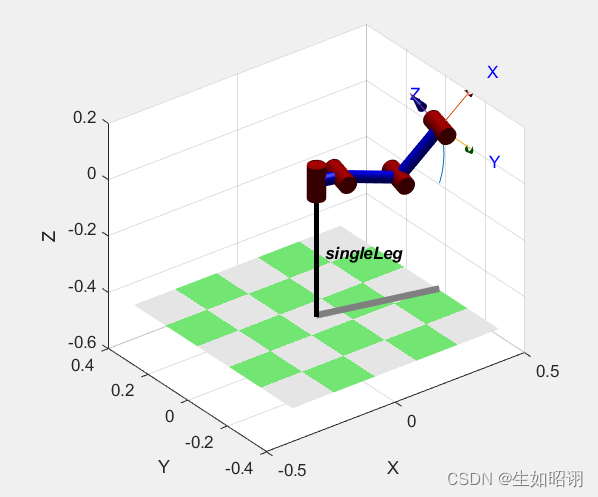
7. 其余函数介绍
-
jacob函数:求解雅克比矩阵

-
ctraj函数:计算在每一步(step)变换时的末端相对于首端的齐次变换矩阵;
-
transl函数:将齐次变换矩阵转换为坐标值;
-
isrevolute函数:测试关节是否可以转动
直线规划、圆规划测试代码:
clear ALL
close ALL
% startup_rvc
% theta表示关节角,d为偏置距离,a为杆长,alpha为杆扭角,sigma为0表示旋转关节
% theta d a alpha sigma 连杆的DH参数
L1 = Link([0 84.72 41.04 pi/2 0]);
L2 = Link([0 0 200 0 0]);
L3 = Link([0 0 214.8 0 0]);
% 限制转动角度
L1.qlim = [deg2rad(-170) deg2rad(170)];
L2.qlim = [deg2rad(-60) deg2rad(85)];
L3.qlim = [deg2rad(-90) deg2rad(10)];
mrbt = SerialLink([L1 L2 L3], 'name', '机械臂仿真');
% 模式1,控制关节角拖动变化
view(3);
mrbt.teach() %调出figure界面模拟控制关节角
% % 模式2,直线规划测试
% T1 = transl(300,220,40); %起点
% T2 = transl(320,-50,220); %终点
% %ctraj 利用匀加速匀减速规划轨迹
% T = ctraj(T1,T2,50);
% Tj = transl(T);
% %输出末端轨迹
% plot3(Tj(:,1),Tj(:,2),Tj(:,3));
% grid on;
%
% %当反解的机器人对象的自由度少于6时,要用mask vector减少自由度
% %无法直接调用ikine作为运动学反解函数
% q = mrbt.ikine(T,'mask',[1 1 1 0 0 0]);
%
% %调整了一下角度,方便观察
% view(113,23);
% mrbt.plot(q,'tilesize',500);
% % 模式3,定义圆
% N = (0:0.5:100)';
% center = [275 150 50];
% radius = 50;
% theta = ( N/N(end) )*2*pi;
% points = (center + radius*[cos(theta) sin(theta) zeros(size(theta))])';
% plot3(points(1,:),points(2,:),points(3,:),'r');
% %
% % pionts矩阵是“横着”的,取其转置矩阵,进一步得到其齐次变换矩阵
% T = transl(points');
% %
% % 当反解的机器人对象的自由度少于6时,要用mask vector进行忽略某个关节自由度
% q = mrbt.ikine(T,'mask',[1 1 1 0 0 0]);
% hold on;
% % 调整了一下角度,方便观察
% view(153,23)
% mrbt.plot(q,'tilesize',500);