机械臂的运动学是研究机械臂各连杆坐标系之间的运动关系，是对机械臂进行运动控制的基础。通过D-H 表示法建立机械臂的运动学数学模型，求得机械臂末端的运动学方程，利用指数积进行实验验证，使用 Matlab Robotics Toolbox 对该机械臂进行运动学仿真建模，并进行实例仿真。通过仿真结果，分析机械臂的运动情况，验证运动学算法的正确性。并采用蒙特卡洛法在 Matlab 环境中求出机械臂的工作空间点云图，为机械臂轨迹规划和控制的研究提供可靠的依据。
机械臂的运动学是研究机械臂各连杆坐标系之间的运动关系，是对机械臂进行运动控制的基础。通过D-H 表示法建立机械臂的运动学数学模型，求得机械臂末端的运动学方程，利用指数积进行实验验证，使用 Matlab Robotics Toolbox 对该机械臂进行运动学仿真建模，并进行实例仿真。通过仿真结果，分析机械臂的运动情况，验证运动学算法的正确性。并采用蒙特卡洛法在 Matlab 环境中求出机械臂的工作空间点云图，为机械臂轨迹规划和控制的研究提供可靠的依据。
D-H 表示法是由 、 、、 四个参数来描述连杆和相连连杆间的关系，其中连杆长度和连杆转角用于描述连杆本身，连杆偏距和关节用于描述相邻连杆间的连接关系。在相邻两个关节坐标系之间，通过以下两个旋转变换和两个平移变换可以建立这两个关节坐标系之间的关系：
(1)绕着 轴旋转，使得轴和轴平行；
(2)沿着轴平移 ，使得轴和轴共线；
(3)绕着 轴旋转，使得 轴和 轴平行；
(4)沿着轴平移，使得 轴和 轴共线。
依据改进 D-H 表示法建立机械臂的连杆坐标系，如图所示。
该机械臂6个关节都是转动关节，前3个关节确定手腕参考点的位置，后3个关节确定手腕的方位。和大多数工业机器人一样，后3个关节轴线交于一点，因此将该点作为手腕的参考点，也选作为连杆坐标系{4},{5}和{6}的原点。在改进D-H坐标系中，{0}和{1}一般重合，O1为轴1和轴2公法线在轴1上的交点，此时关节1和关节2在z方向上的偏置没有体现出来，对于整个机械臂各关节的相对运动来说并没有影响。先建立改进D-H坐标系如下：
表 5.1 机械臂的 D-H 参数表
|
连杆 i |
关节变量 |
扭转角 |
连杆长度mm |
连杆偏置mm |
变量范围 |
|
1 |
0h |
0° |
0 |
0 |
-160°~+160° |
|
2 |
02 |
-90° |
0 |
390 |
-225°~+45° |
|
3 |
03 |
0° |
350 |
0 |
-45°~225° |
|
4 |
04 |
-90° |
130 |
393 |
-350°~+350° |
|
5 |
05 |
90° |
0 |
0 |
-122.5°~122.5° |
|
6 |
06 |
-90° |
0 |
0 |
-350°~350° |
|
相邻两个连杆之间的齐次变换矩阵 是以上 4 个运动变化矩阵的乘积，由于所有变换都在相对的坐标系进行的，因此这 4 个变化矩阵都是右乘的，由连杆的齐次变换矩阵式(5.1)和表 5.1 的连杆参数，运用 D-H 表示法求得各连杆的变换矩阵如下：
，
机械臂末端对基座的总变换矩阵为
机械臂运动学仿真Matlab Robotics Toolbox 是一个功能强大的机器人工具箱，可以对机械臂运动学、动力学和轨迹规划等方面进行模拟仿真。通过 Matlab Robotics Toolbox 中的程序命令可以生成六自由度机械臂的运动学仿真模型以及控制各关节角度的控制面板，在控制面板中可以通过调节机械臂各关节的角度参数，使机械臂达到指定的位姿。机械臂的运动学仿真模型和控制面板如图 5.3 所示。
可以通过MATLAB Robotics Toolbox生成六自由度机器人的三维模型， 同时生成机器人控制面板， 控制面板可以调节各关节的角度， 从而使关节产生转动。控制面板和生成模型如图所示
指数积公式求解位移
利用PoE公式对机器人进行正运动学的求解，建立基坐标系{S}和{T}，并取机器人完全展开时的位形为初始位形，初始位形时基座坐标系与工具坐标系的坐标系，
各关节的单位运动旋量为
，，
，，，
对于旋转关节，有
，，
这与用DH参数法求解的结果是一致的，也证明了结果的正确性。
-
- 机械臂工作空间分析
机械臂的工作空间是反映机械臂灵活性的一个重要指标。理论上六自由度机械臂的工作空间是一个近似球形区域，能够覆盖机械臂所在的位置，但由于机械臂关节的运动范围受到限制，机械臂末端会存在一些不能到达的工作死区，使得机械臂的工作范围和灵活性受到限制。所以对机械臂的工作空间进行分析，对合理安排机械臂的安装位置和工作任务是十分重要的。将机械臂的工作空间记作。则关节变量和工作空间的关系可以用下式表示：
其中：表示关节变量， 表示空间约束，Q 不能随意取值，需要考虑实际情况确定约束空间：和分别表示关节转动范围的下限和上限。因此，机械臂的工作空间区域可以表示
蒙特卡罗法是一种广泛应用的数值计算方法，通过借助重复随机抽样的方法求解数学问题。蒙特卡罗法计算速度快、工作量少，可以避免复杂的数学推导和计算过程， 而且能够方便的使用计算机实现图形的精确绘制，在 Matlab 环境下，基于蒙特卡罗法求解机械臂工作空间的步骤如下：
1、对机械臂进行正运动学分析，计算出机械臂末端相对于基坐标的位置向量
2、利用rand( 1)函数，生成各个关节变量定义区间内的随机值，即
3、将步骤(2)中生成的关节变量代入正运动学方程，求出机械臂末端的位置坐标点。位置坐标点数越多，越能精确反映出机械臂的实际工作空间。
本章分析了所设计的六自由度机械臂的运动学。首先利用改进的 D-H 表示法建立了机械臂的连杆坐标系，求得了连杆的变换矩阵，进而推导出机械臂的运动学正解， 在此基础上利用代数解法对运动学逆问题进行求解。然后利用 Matlab Robotics Toolbox 工具箱对机械臂进行了运动学的仿真验证，得到了机械臂的仿真模型以及机械臂末端的运动情况。最后基于蒙特卡洛法得到了机械臂的工作空间云图，确定了机械臂的工作空间范围。
D-H 表示法是由 、 、、 四个参数来描述连杆和相连连杆间的关系，其中连杆长度和连杆转角用于描述连杆本身，连杆偏距和关节用于描述相邻连杆间的连接关系。在相邻两个关节坐标系之间，通过以下两个旋转变换和两个平移变换可以建立这两个关节坐标系之间的关系：
(1)绕着 轴旋转，使得轴和轴平行；
(2)沿着轴平移 ，使得轴和轴共线；
(3)绕着 轴旋转，使得 轴和 轴平行；
(4)沿着轴平移，使得 轴和 轴共线。
依据改进 D-H 表示法建立机械臂的连杆坐标系，如图所示。
该机械臂6个关节都是转动关节，前3个关节确定手腕参考点的位置，后3个关节确定手腕的方位。和大多数工业机器人一样，后3个关节轴线交于一点，因此将该点作为手腕的参考点，也选作为连杆坐标系{4},{5}和{6}的原点。在改进D-H坐标系中，{0}和{1}一般重合，O1为轴1和轴2公法线在轴1上的交点，此时关节1和关节2在z方向上的偏置没有体现出来，对于整个机械臂各关节的相对运动来说并没有影响。先建立改进D-H坐标系如下：
表 5.1 机械臂的 D-H 参数表
|
连杆 i |
关节变量 |
扭转角 |
连杆长度mm |
连杆偏置mm |
变量范围 |
|
1 |
0h |
0° |
0 |
0 |
-160°~+160° |
|
2 |
02 |
-90° |
0 |
390 |
-225°~+45° |
|
3 |
03 |
0° |
350 |
0 |
-45°~225° |
|
4 |
04 |
-90° |
130 |
393 |
-350°~+350° |
|
5 |
05 |
90° |
0 |
0 |
-122.5°~122.5° |
|
6 |
06 |
-90° |
0 |
0 |
-350°~350° |
|
相邻两个连杆之间的齐次变换矩阵 是以上 4 个运动变化矩阵的乘积，由于所有变换都在相对的坐标系进行的，因此这 4 个变化矩阵都是右乘的，由连杆的齐次变换矩阵式(5.1)和表 5.1 的连杆参数，运用 D-H 表示法求得各连杆的变换矩阵如下：
，
机械臂末端对基座的总变换矩阵为
机械臂运动学仿真Matlab Robotics Toolbox 是一个功能强大的机器人工具箱，可以对机械臂运动学、动力学和轨迹规划等方面进行模拟仿真。通过 Matlab Robotics Toolbox 中的程序命令可以生成六自由度机械臂的运动学仿真模型以及控制各关节角度的控制面板，在控制面板中可以通过调节机械臂各关节的角度参数，使机械臂达到指定的位姿。机械臂的运动学仿真模型和控制面板如图 5.3 所示。
可以通过MATLAB Robotics Toolbox生成六自由度机器人的三维模型， 同时生成机器人控制面板， 控制面板可以调节各关节的角度， 从而使关节产生转动。控制面板和生成模型如图所示
指数积公式求解位移正解
利用PoE公式对机器人进行正运动学的求解，建立基坐标系{S}和{T}，并取机器人完全展开时的位形为初始位形，初始位形时基座坐标系与工具坐标系的坐标系，
各关节的单位运动旋量为
，，
，，，
对于旋转关节，有
，，
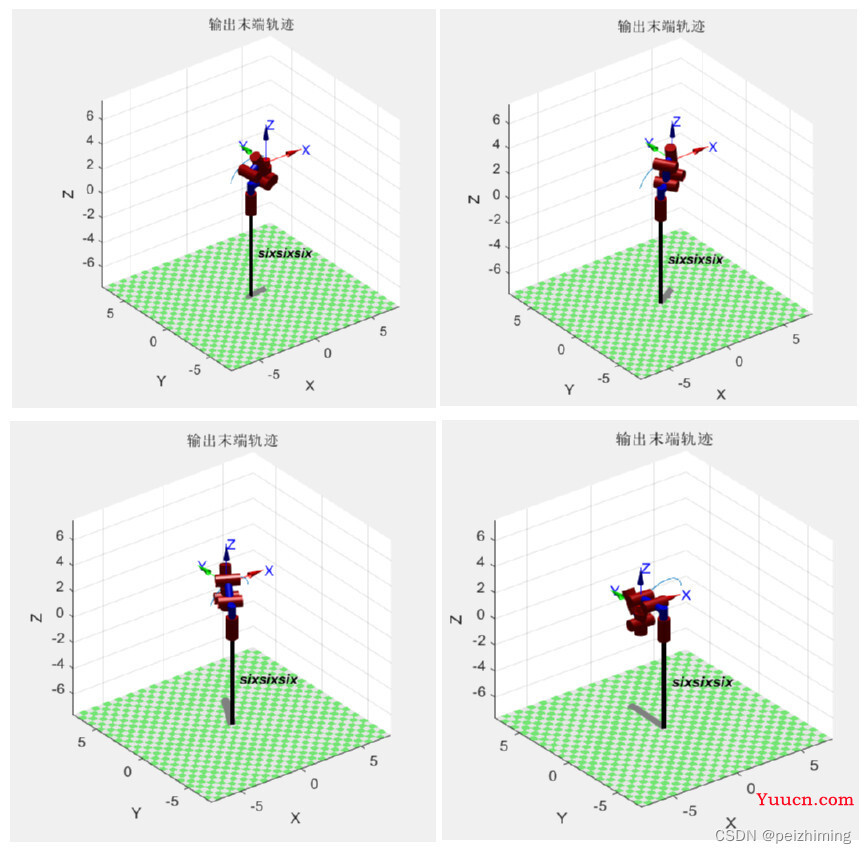
这与用DH参数法求解的结果是一致的，也证明了结果的正确性。
-
- 机械臂工作空间分析
机械臂的工作空间是反映机械臂灵活性的一个重要指标。理论上六自由度机械臂的工作空间是一个近似球形区域，能够覆盖机械臂所在的位置，但由于机械臂关节的运动范围受到限制，机械臂末端会存在一些不能到达的工作死区，使得机械臂的工作范围和灵活性受到限制。所以对机械臂的工作空间进行分析，对合理安排机械臂的安装位置和工作任务是十分重要的。将机械臂的工作空间记作。则关节变量和工作空间的关系可以用下式表示：
其中：表示关节变量， 表示空间约束，Q 不能随意取值，需要考虑实际情况确定约束空间：和分别表示关节转动范围的下限和上限。因此，机械臂的工作空间区域可以表示
蒙特卡罗法是一种广泛应用的数值计算方法，通过借助重复随机抽样的方法求解数学问题。蒙特卡罗法计算速度快、工作量少，可以避免复杂的数学推导和计算过程， 而且能够方便的使用计算机实现图形的精确绘制，在 Matlab 环境下，基于蒙特卡罗法求解机械臂工作空间的步骤如下：
1、对机械臂进行正运动学分析，计算出机械臂末端相对于基坐标的位置向量
2、利用rand( 1)函数，生成各个关节变量定义区间内的随机值，即
3、将步骤(2)中生成的关节变量代入正运动学方程，求出机械臂末端的位置坐标点。位置坐标点数越多，越能精确反映出机械臂的实际工作空间。
本章分析了所设计的六自由度机械臂的运动学。首先利用改进的 D-H 表示法建立了机械臂的连杆坐标系，求得了连杆的变换矩阵，进而推导出机械臂的运动学正解， 在此基础上利用代数解法对运动学逆问题进行求解。然后利用 Matlab Robotics Toolbox 工具箱对机械臂进行了运动学的仿真验证，得到了机械臂的仿真模型以及机械臂末端的运动情况。最后基于蒙特卡洛法得到了机械臂的工作空间云图，确定了机械臂的工作空间范围。