一、混淆矩阵

对于二分类的模型，预测结果与实际结果分别可以取0和1。我们用N和P代替0和1，T和F表示预测正确和错误。将他们两两组合，就形成了下图所示的混淆矩阵（注意：组合结果都是针对预测结果而言的）。

由于1和0是数字，阅读性不好，所以我们分别用P和N表示1和0两种结果。变换之后为PP，PN，NP，NN，阅读性也很差，我并不能轻易地看出来预测的正确性与否。因此，为了能够更清楚地分辨各种预测情况是否正确，我们将其中一个符号修改为T和F，以便于分辨出结果。

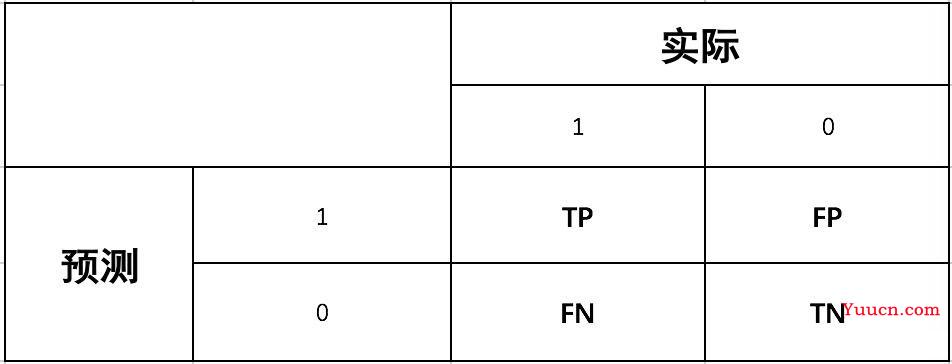
• P（Positive）：代表 1
• N（Negative）：代表 0
• T（True）：代表预测正确
• F（False）：代表预测错误

二、准确率、精确率、召回率、F1-Measure

• 准确率(Accuracy)：对于给定的测试数据集，分类器正确分类的样本数与总样本数之比。
  
  A
  c
  c
  u
  r
  a
  c
  y
  =
  T
  P
  +
  T
  N
  T
  P
  +
  T
  N
  +
  F
  P
  +
  F
  N
  =
  T
  P
  +
  T
  N
  总
  样
  本
  数
  量
  Accuracy=\cfrac{TP+TN}{TP+TN+FP+FN}=\cfrac{TP+TN}{总样本数量}
  Accuracy=TP+TN+FP+FNTP+TN​=总样本数量TP+TN​
• 精确率(Precision)**：精指分类正确的正样本个数（TP）占分类器判定为正样本的样本个数（TP+FP）的比例。
  
  P
  r
  e
  c
  i
  s
  i
  o
  n
  =
  T
  P
  T
  P
  +
  F
  P
  =
  分
  类
  正
  确
  的
  正
  样
  本
  个
  数
  判
  定
  为
  正
  样
  本
  的
  样
  本
  个
  数
  Precision=\cfrac{TP}{TP+FP}=\cfrac{分类正确的正样本个数}{判定为正样本的样本个数}
  Precision=TP+FPTP​=判定为正样本的样本个数分类正确的正样本个数​
• 召回率(Recall)：召回率是指分类正确的正样本个数（TP）占真正的正样本个数（TP+FN）的比例。
  
  R
  e
  c
  a
  l
  l
  =
  T
  P
  T
  P
  +
  F
  N
  =
  分
  类
  正
  确
  的
  正
  样
  本
  个
  数
  全
  部
  真
  正
  的
  正
  样
  本
  个
  数
  Recall=\cfrac{TP}{TP+FN}=\cfrac{分类正确的正样本个数}{全部真正的正样本个数}
  Recall=TP+FNTP​=全部真正的正样本个数分类正确的正样本个数​
• F1-Measure值：就是精确率和召回率的调和平均值。
  
  F
  1
  −
  M
  e
  a
  s
  u
  r
  e
  =
  2
  1
  P
  r
  e
  c
  i
  s
  i
  o
  n
  +
  1
  R
  e
  c
  a
  l
  l
  =
  2
  ×
  P
  r
  e
  c
  i
  s
  i
  o
  n
  ×
  R
  e
  c
  a
  l
  l
  P
  r
  e
  c
  i
  s
  i
  o
  n
  +
  R
  e
  c
  a
  l
  l
  \begin{aligned}F1-Measure=\cfrac{2}{\cfrac{1}{Precision}+\cfrac{1}{Recall}}=\cfrac{2×Precision×Recall}{Precision+Recall}\end{aligned}
  F1−Measure=Precision1​+Recall1​2​=Precision+Recall2×Precision×Recall​​

每个评估指标都有其价值，但如果只从单一的评估指标出发去评估模型，往往会得出片面甚至错误的结论；只有通过一组互补的指标去评估模型，才能更好地发现并解决模型存在的问题，从而更好地解决实际业务场景中遇到的问题。

三、多分类评价指标-案例

假设有如下的数据

预测	真实
A	A
A	A
B	A
C	A
B	B
B	B
C	B
B	C
C	C

可以看出，上表为一份样本量为9，类别数为3的含标注结果的三分类预测样本。TN对于准召的计算而言是不需要的，因此下面的表格中未统计该值。

1、按照定义计算Precision、Recall

1.1 对于类别A

TP = 2	FP = 0
FN = 2	TN = ~

P
r
e
c
i
s
i
o
n
=
T
P
T
P
+
F
P
=
分
类
正
确
的
正
样
本
个
数
判
定
为
正
样
本
的
样
本
个
数
=
2
2
+
=
100
%
=
1.0
Precision=\cfrac{TP}{TP+FP}=\cfrac{分类正确的正样本个数}{判定为正样本的样本个数}=\cfrac{2}{2+0}=100\%=1.0
Precision=TP+FPTP​=判定为正样本的样本个数分类正确的正样本个数​=2+02​=100%=1.0

R
e
c
a
l
l
=
T
P
T
P
+
F
N
=
分
类
正
确
的
正
样
本
个
数
真
正
的
正
样
本
个
数
=
2
2
+
2
=
50
%
=
0.5
Recall=\cfrac{TP}{TP+FN}=\cfrac{分类正确的正样本个数}{真正的正样本个数}=\cfrac{2}{2+2}=50\%=0.5
Recall=TP+FNTP​=真正的正样本个数分类正确的正样本个数​=2+22​=50%=0.5

1.2 对于类别B

TP = 2	FP = 2
FN = 1	TN = ~

P
r
e
c
i
s
i
o
n
=
T
P
T
P
+
F
P
=
分
类
正
确
的
正
样
本
个
数
判
定
为
正
样
本
的
样
本
个
数
=
2
2
+
2
=
50
%
=
0.5
Precision=\cfrac{TP}{TP+FP}=\cfrac{分类正确的正样本个数}{判定为正样本的样本个数}=\cfrac{2}{2+2}=50\%=0.5
Precision=TP+FPTP​=判定为正样本的样本个数分类正确的正样本个数​=2+22​=50%=0.5

R
e
c
a
l
l
=
T
P
T
P
+
F
N
=
分
类
正
确
的
正
样
本
个
数
真
正
的
正
样
本
个
数
=
2
2
+
1
=
67
%
=
0.67
Recall=\cfrac{TP}{TP+FN}=\cfrac{分类正确的正样本个数}{真正的正样本个数}=\cfrac{2}{2+1}=67\%=0.67
Recall=TP+FNTP​=真正的正样本个数分类正确的正样本个数​=2+12​=67%=0.67

1.3 对于类别C

TP = 1	FP = 2
FN = 1	TN = ~

P
r
e
c
i
s
i
o
n
=
T
P
T
P
+
F
P
=
分
类
正
确
的
正
样
本
个
数
判
定
为
正
样
本
的
样
本
个
数
=
1
1
+
2
=
33
%
=
0.33
Precision=\cfrac{TP}{TP+FP}=\cfrac{分类正确的正样本个数}{判定为正样本的样本个数}=\cfrac{1}{1+2}=33\%=0.33
Precision=TP+FPTP​=判定为正样本的样本个数分类正确的正样本个数​=1+21​=33%=0.33

R
e
c
a
l
l
=
T
P
T
P
+
F
N
=
分
类
正
确
的
正
样
本
个
数
真
正
的
正
样
本
个
数
=
1
1
+
1
=
50
%
=
0.5
Recall=\cfrac{TP}{TP+FN}=\cfrac{分类正确的正样本个数}{真正的正样本个数}=\cfrac{1}{1+1}=50\%=0.5
Recall=TP+FNTP​=真正的正样本个数分类正确的正样本个数​=1+11​=50%=0.5

2、调用sklearn的api进行验证

from sklearn.metrics import classification_report
from sklearn.metrics import precision_score, recall_score, f1_score
true_lable = [0, 0, 0, 0, 1, 1, 1, 2, 2]
prediction = [0, 0, 1, 2, 1, 1, 2, 1, 2]
measure_result = classification_report(true_lable, prediction)
print('measure_result = \n', measure_result)

打印结果：

measure_result =
               precision    recall  f1-score   support
           0       1.00      0.50      0.67         4
           1       0.50      0.67      0.57         3
           2       0.33      0.50      0.40         2
    accuracy                           0.56         9
   macro avg       0.61      0.56      0.55         9
weighted avg       0.69      0.56      0.58         9

四、Micro-F1、Macro-F1、weighted-F1

总的来说，微观F1(micro-F1)和宏观F1(macro-F1)都是F1合并后的结果，这两个F1都是用在多分类任务中的评价指标，是两种不一样的求F1均值的方式；micro-F1和macro-F1的计算方法有差异，得出来的结果也略有差异；

1、Micro-F1

Micro-F1 不需要区分类别，直接使用总体样本的准召计算f1 score。

• 计算方法：先计算所有类别的总的Precision和Recall，然后计算出来的F1值即为micro-F1；

• 使用场景：在计算公式中考虑到了每个类别的数量，所以适用于数据分布不平衡的情况；但同时因为考虑到数据的数量，所以在数据极度不平衡的情况下，数量较多数量的类会较大的影响到F1的值；

该样本的混淆矩阵如下：

TP = 5	FP = 4
FN = 2	TN = ~

P
r
e
c
i
s
i
o
n
=
T
P
T
P
+
F
P
=
分
类
正
确
的
正
样
本
个
数
判
定
为
正
样
本
的
样
本
个
数
=
5
5
+
4
=
55.56
%
=
0.5556
Precision=\cfrac{TP}{TP+FP}=\cfrac{分类正确的正样本个数}{判定为正样本的样本个数}=\cfrac{5}{5+4}=55.56\%=0.5556
Precision=TP+FPTP​=判定为正样本的样本个数分类正确的正样本个数​=5+45​=55.56%=0.5556

R
e
c
a
l
l
=
T
P
T
P
+
F
N
=
分
类
正
确
的
正
样
本
个
数
真
正
的
正
样
本
个
数
=
5
5
+
4
=
55.56
%
=
0.5556
Recall=\cfrac{TP}{TP+FN}=\cfrac{分类正确的正样本个数}{真正的正样本个数}=\cfrac{5}{5+4}=55.56\%=0.5556
Recall=TP+FNTP​=真正的正样本个数分类正确的正样本个数​=5+45​=55.56%=0.5556

F
1
−
M
e
a
s
u
r
e
=
2
1
P
r
e
c
i
s
i
o
n
+
1
R
e
c
a
l
l
=
2
×
P
r
e
c
i
s
i
o
n
×
R
e
c
a
l
l
P
r
e
c
i
s
i
o
n
+
R
e
c
a
l
l
=
2
×
0.5556
×
0.5556
0.5556
+
0.5556
=
0.5556
\begin{aligned}F1-Measure=\cfrac{2}{\cfrac{1}{Precision}+\cfrac{1}{Recall}}=\cfrac{2×Precision×Recall}{Precision+Recall}=\cfrac{2×0.5556×0.5556}{0.5556+0.5556}=0.5556\end{aligned}
F1−Measure=Precision1​+Recall1​2​=Precision+Recall2×Precision×Recall​=0.5556+0.55562×0.5556×0.5556​=0.5556​

2、Macro-F1

不同于micro f1，macro f1需要先计算出每一个类别的准召及其f1 score，然后通过求均值得到在整个样本上的f1 score。

• 计算方法：将所有类别的Precision和Recall求平均，然后计算F1值作为macro-F1；
• 使用场景：没有考虑到数据的数量，所以会平等的看待每一类（因为每一类的precision和recall都在0-1之间），会相对受高precision和高recall类的影响较大；

类别A的​：

F
1
−
A
=
2
×
P
r
e
c
i
s
i
o
n
×
R
e
c
a
l
l
P
r
e
c
i
s
i
o
n
+
R
e
c
a
l
l
=
2
×
1
×
0.5
1
+
0.5
=
0.6667
\begin{aligned}F1-A=\cfrac{2×Precision×Recall}{Precision+Recall}=\cfrac{2×1×0.5}{1+0.5}=0.6667\end{aligned}
F1−A=Precision+Recall2×Precision×Recall​=1+0.52×1×0.5​=0.6667​

类别B的​：

F
1
−
B
=
2
×
P
r
e
c
i
s
i
o
n
×
R
e
c
a
l
l
P
r
e
c
i
s
i
o
n
+
R
e
c
a
l
l
=
2
×
0.5
×
0.67
0.5
+
0.67
=
0.57265
\begin{aligned}F1-B=\cfrac{2×Precision×Recall}{Precision+Recall}=\cfrac{2×0.5×0.67}{0.5+0.67}=0.57265\end{aligned}
F1−B=Precision+Recall2×Precision×Recall​=0.5+0.672×0.5×0.67​=0.57265​

类别C的​：

F
1
−
C
=
2
×
P
r
e
c
i
s
i
o
n
×
R
e
c
a
l
l
P
r
e
c
i
s
i
o
n
+
R
e
c
a
l
l
=
2
×
0.33
×
0.5
0.33
+
0.5
=
0.39759
\begin{aligned}F1-C=\cfrac{2×Precision×Recall}{Precision+Recall}=\cfrac{2×0.33×0.5}{0.33+0.5}=0.39759\end{aligned}
F1−C=Precision+Recall2×Precision×Recall​=0.33+0.52×0.33×0.5​=0.39759​

Macro-F1为上面三者的平均值：

M
a
c
r
o
−
F
1
=
F
1
−
A
+
F
1
−
B
+
F
1
−
C
3
=
0.6667
+
0.57265
+
0.39759
3
=
0.546
\begin{aligned}Macro-F1=\cfrac{F1-A + F1-B + F1-C}{3}=\cfrac{0.6667 + 0.57265 + 0.39759}{3}=0.546\end{aligned}
Macro−F1=3F1−A+F1−B+F1−C​=30.6667+0.57265+0.39759​=0.546​

3、weighted-F1

除了micro-F1和macro-F1，还有weighted-F1，是一个将F1-score乘以该类的比例之后相加的结果，也可以看做是macro-F1的变体吧。

weighted-F1和macro-F1的区别在于：macro-F1对每一类都赋予了相同的权重，而weighted-F1则根据每一类的比例分别赋予不同的权重。

五、指标的选择问题

“我们看到，对于 Macro 来说， 小类别相当程度上拉高了 Precision 的值，而实际上， 并没有那么多样本被正确分类，考虑到实际的环境中，真实样本分布和训练样本分布相同的情况下，这种指标明显是有问题的， 小类别起到的作用太大，以至于大样本的分类情况不佳。 而对于 Micro 来说，其考虑到了这种样本不均衡的问题， 因此在这种情况下相对较佳。

总的来说， 如果你的类别比较均衡，则随便； 如果你认为大样本的类别应该占据更重要的位置， 使用Micro； 如果你认为小样本也应该占据重要的位置，则使用 Macro； 如果 Micro << Macro ， 则意味着在大样本类别中出现了严重的分类错误； 如果 Macro << Micro ， 则意味着小样本类别中出现了严重的分类错误。

为了解决 Macro 无法衡量样本均衡问题，一个很好的方法是求加权的 Macro， 因此 Weighed F1 出现了。”

六、代码

1、数据01

true_lable = [0, 0, 0, 0, 1, 1, 1, 2, 2]
prediction = [0, 0, 1, 2, 1, 1, 2, 1, 2]

from sklearn.metrics import classification_report
from sklearn.metrics import precision_score, recall_score, f1_score
true_lable = [0, 0, 0, 0, 1, 1, 1, 2, 2]
prediction = [0, 0, 1, 2, 1, 1, 2, 1, 2]
measure_result = classification_report(true_lable, prediction)
print('measure_result = \n', measure_result)
print("----------------------------- precision（精确率）-----------------------------")
precision_score_average_None = precision_score(true_lable, prediction, average=None)
precision_score_average_micro = precision_score(true_lable, prediction, average='micro')
precision_score_average_macro = precision_score(true_lable, prediction, average='macro')
precision_score_average_weighted = precision_score(true_lable, prediction, average='weighted')
print('precision_score_average_None = ', precision_score_average_None)
print('precision_score_average_micro = ', precision_score_average_micro)
print('precision_score_average_macro = ', precision_score_average_macro)
print('precision_score_average_weighted = ', precision_score_average_weighted)
print("\n\n----------------------------- recall（召回率）-----------------------------")
recall_score_average_None = recall_score(true_lable, prediction, average=None)
recall_score_average_micro = recall_score(true_lable, prediction, average='micro')
recall_score_average_macro = recall_score(true_lable, prediction, average='macro')
recall_score_average_weighted = recall_score(true_lable, prediction, average='weighted')
print('recall_score_average_None = ', recall_score_average_None)
print('recall_score_average_micro = ', recall_score_average_micro)
print('recall_score_average_macro = ', recall_score_average_macro)
print('recall_score_average_weighted = ', recall_score_average_weighted)
print("\n\n----------------------------- F1-value-----------------------------")
f1_score_average_None = f1_score(true_lable, prediction, average=None)
f1_score_average_micro = f1_score(true_lable, prediction, average='micro')
f1_score_average_macro = f1_score(true_lable, prediction, average='macro')
f1_score_average_weighted = f1_score(true_lable, prediction, average='weighted')
print('f1_score_average_None = ', f1_score_average_None)
print('f1_score_average_micro = ', f1_score_average_micro)
print('f1_score_average_macro = ', f1_score_average_macro)
print('f1_score_average_weighted = ', f1_score_average_weighted)

打印结果：

measure_result =
               precision    recall  f1-score   support
           0       1.00      0.50      0.67         4
           1       0.50      0.67      0.57         3
           2       0.33      0.50      0.40         2
    accuracy                           0.56         9
   macro avg       0.61      0.56      0.55         9
weighted avg       0.69      0.56      0.58         9
----------------------------- precision（精确率）-----------------------------
precision_score_average_None =  [1.         0.5        0.33333333]
precision_score_average_micro =  0.5555555555555556
precision_score_average_macro =  0.611111111111111
precision_score_average_weighted =  0.6851851851851852
----------------------------- recall（召回率）-----------------------------
recall_score_average_None =  [0.5        0.66666667 0.5       ]
recall_score_average_micro =  0.5555555555555556
recall_score_average_macro =  0.5555555555555555
recall_score_average_weighted =  0.5555555555555556
----------------------------- F1-value-----------------------------
f1_score_average_None =  [0.66666667 0.57142857 0.4       ]
f1_score_average_micro =  0.5555555555555556
f1_score_average_macro =  0.546031746031746
f1_score_average_weighted =  0.5756613756613757
Process finished with exit code 0

2、数据02

true_lable = [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3]
prediction = [3, 0, 0, 0, 0, 0, 0, 0, 2, 3, 3, 1, 1, 1, 1, 1, 1, 3, 1, 2, 2, 2, 2, 2, 3, 0, 3, 3, 3, 3]

from sklearn.metrics import classification_report
from sklearn.metrics import precision_score, recall_score, f1_score
true_lable = [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3]
prediction = [3, 0, 0, 0, 0, 0, 0, 0, 2, 3, 3, 1, 1, 1, 1, 1, 1, 3, 1, 2, 2, 2, 2, 2, 3, 0, 3, 3, 3, 3]
measure_result = classification_report(true_lable, prediction)
print('measure_result = \n', measure_result)
print("----------------------------- precision（精确率）-----------------------------")
precision_score_average_None = precision_score(true_lable, prediction, average=None)
precision_score_average_micro = precision_score(true_lable, prediction, average='micro')
precision_score_average_macro = precision_score(true_lable, prediction, average='macro')
precision_score_average_weighted = precision_score(true_lable, prediction, average='weighted')
print('precision_score_average_None = ', precision_score_average_None)
print('precision_score_average_micro = ', precision_score_average_micro)
print('precision_score_average_macro = ', precision_score_average_macro)
print('precision_score_average_weighted = ', precision_score_average_weighted)
print("\n\n----------------------------- recall（召回率）-----------------------------")
recall_score_average_None = recall_score(true_lable, prediction, average=None)
recall_score_average_micro = recall_score(true_lable, prediction, average='micro')
recall_score_average_macro = recall_score(true_lable, prediction, average='macro')
recall_score_average_weighted = recall_score(true_lable, prediction, average='weighted')
print('recall_score_average_None = ', recall_score_average_None)
print('recall_score_average_micro = ', recall_score_average_micro)
print('recall_score_average_macro = ', recall_score_average_macro)
print('recall_score_average_weighted = ', recall_score_average_weighted)
print("\n\n----------------------------- F1-value-----------------------------")
f1_score_average_None = f1_score(true_lable, prediction, average=None)
f1_score_average_micro = f1_score(true_lable, prediction, average='micro')
f1_score_average_macro = f1_score(true_lable, prediction, average='macro')
f1_score_average_weighted = f1_score(true_lable, prediction, average='weighted')
print('f1_score_average_None = ', f1_score_average_None)
print('f1_score_average_micro = ', f1_score_average_micro)
print('f1_score_average_macro = ', f1_score_average_macro)
print('f1_score_average_weighted = ', f1_score_average_weighted)

打印结果：

measure_result =
               precision    recall  f1-score   support
           0       0.88      0.78      0.82         9
           1       0.86      0.75      0.80         8
           2       0.83      0.71      0.77         7
           3       0.56      0.83      0.67         6
    accuracy                           0.77        30
   macro avg       0.78      0.77      0.76        30
weighted avg       0.80      0.77      0.77        30
----------------------------- precision（精确率）-----------------------------
precision_score_average_None =  [0.875      0.85714286 0.83333333 0.55555556]
precision_score_average_micro =  0.7666666666666667
precision_score_average_macro =  0.7802579365079365
precision_score_average_weighted =  0.7966269841269841
----------------------------- recall（召回率）-----------------------------
recall_score_average_None =  [0.77777778 0.75       0.71428571 0.83333333]
recall_score_average_micro =  0.7666666666666667
recall_score_average_macro =  0.7688492063492064
recall_score_average_weighted =  0.7666666666666667
----------------------------- F1-value-----------------------------
f1_score_average_None =  [0.82352941 0.8        0.76923077 0.66666667]
f1_score_average_micro =  0.7666666666666667
f1_score_average_macro =  0.7648567119155354
f1_score_average_weighted =  0.7732126696832579
Process finished with exit code 0

参考资料：
Macro-F1 Score与Micro-F1 Score
分类问题的几个评价指标（Precision、Recall、F1-Score、Micro-F1、Macro-F1）
分类问题中的各种评价指标——precision，recall，F1-score，macro-F1，micro-F1