有限状态机
写RTL的时候,实现一个功能的时候有很多种方法
- 将系统划分为多个状态,状态之间有状态的转移,第一步,第二步,,,,形成有限状态机
- 流水线技术设计,从输入到输出有多个步骤
有限状态机,状态是有限的,比如8个状态,16个状态等,在进行设计的时候,状态机的状态不要太多,状态超过10个,就会造成设计复杂度和验证复杂度都变高.
有限状态机分类
- Moore FSM
输出只与当前的状态有关,与输入没有关系 - Mealy FSM
输出不仅与当前的状态有关,还与输入有关
Moore FSM-设计自动售货机
分析输入输出信号
- 自动售货机,输入的就是硬币,输出的是饮料和找零 (确定输入,输出)

- 假设饮料只有一种价格2.5元,输入的零钱只有一元和五角(两种状态,用1bit表示),找零的情况只有两种0元和5角(用1bit表示)(确定输出输出的状态,用几位的信号表示)
定义接口
- 状态机要存储一些状态,肯定会有一些寄存器,会有时钟和复位信号

- 在设计一个模块的时候,最先确定输入输出的端口和位宽以及时序
定义时序
- 输入的一元和五角不能同时为1(确定输入的约束)
内部实现--画出状态转移图
要存储当前已经存储了多少钱,初始状态时0,可以收到1元和5角

- IDLE就是当前系统是空闲状态,没有收到任何的投币
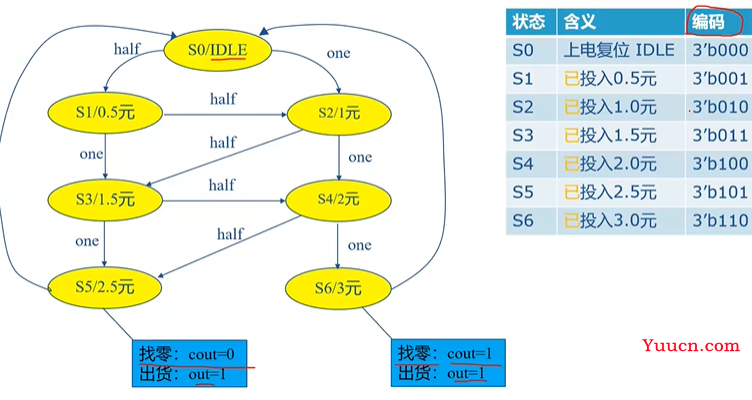
- 这是一个Moore类型的有限状态机,输出只与当前的状态有关
Moore有限状态机电路特点
- 输入与当前的状态有关,所以需要一个寄存器存储当前的状态
- 寄存器存储的状态输入给组合逻辑之后,进行输出
- 输入与当前的状态值,经过组合逻辑之后,输入给寄存器
- 时序清晰,输入和输出,没有一条直接的组合逻辑路径;如果输入经过组合逻辑,没有经过寄存器,直接输出,这样的设计不好;因为不知道周围环境的组合逻辑的时序是多少

Code
module drink_status_moore(
input clk,
input reset,
input half,
input one,
output out,
output cout
);
parameter [2:0] s0 = 3'b000,
s1 = 3'b001,
s2 = 3'b010,
s3 = 3'b011,
s4 = 3'b100,
s5 = 3'b101,
s6 = 3'b110; //定义6个状态
reg [2:0] curr_state; //当前状态 CS
reg [2:0] next_state; //下一个状态 NS reg定义的信号不一定是寄存器
//第一段:声明一个寄存器,state transfer
always @ (posedge clk ,negedge reset) begin
if(~reset)
curr_state <= s0; //这里时钟来了之后,就寄存器传输,寄存器功耗比较大,需要给寄存器传输添加条件
else
curr_state <= #1 next_state;
end
//第二段,根据条件写出中间状态转移
always @ (curr_state,half,one) begin
case(curr_state)
s0:begin
if(half) next_state = s1; //如果两个投币口,就会出现问题,一次投入可能为1.5元,所以要给输入添加约束
else of(one) next_state = s2; //文件和文件之间需要进行一些约束
else next_state = S0;
end
s1:begin
if(half) next_state = s2;
else of(one) next_state = s3;
else next_state = S1;
end
s2:begin
if(half) next_state = s3;
else of(one) next_state = s4;
else next_state = S2;
end
s3:begin
if(half) next_state = s4;
else of(one) next_state = s5;
else next_state = S3;
end
s4:begin
if(half) next_state = s5;
else of(one) next_state = s6;
else next_state = S4;
end
s5:begin
next_state = s0;
end
s6:begin
next_state = s0;
end
default: next_state = s0;
end
//第三段,写出输出
assign out = (curr_state == s5) || (curr_State = s6) ? 1:0;
assign cout = (curr_state == s6) ? 1:0;
endmodule
FSM 三段式的书写方式
mealy FSM-自动售货机
- 相当于在当前状态,考虑之后输入的状态
- 输入经过组合逻辑之后直接得到输出
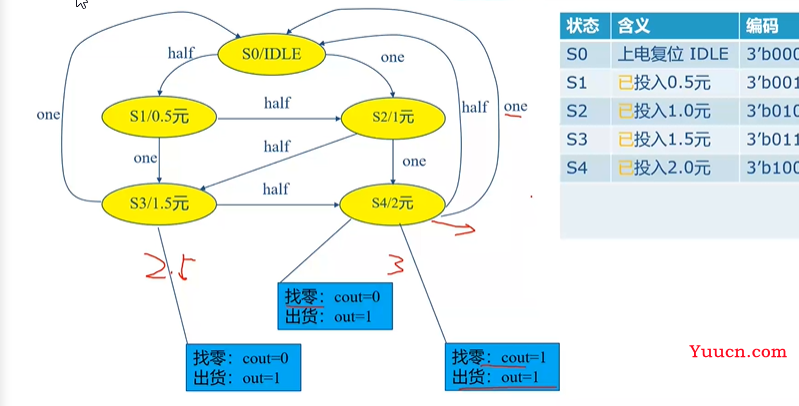
module drink_status_moore(
input clk,
input reset,
input half,
input one,
output out,
output cout
);
parameter [2:0] s0 = 3'b000,
s1 = 3'b001,
s2 = 3'b010,
s3 = 3'b011,
s4 = 3'b100; //定义6个状态,变量名需要更加具有含义
reg [2:0] curr_state; //当前状态 CS
reg [2:0] next_state; //下一个状态 NS reg定义的信号不一定是寄存器
//第一段:声明一个寄存器,state transfer
always @ (posedge clk ,negedge reset) begin
if(~reset)
curr_state <= s0; //这里时钟来了之后,就寄存器传输,寄存器功耗比较大,需要给寄存器传输添加条件
else
curr_state <= #1 next_state;
end
//第二段,根据条件写出中间状态转移
always @ (*) begin
case(curr_state)
s0:begin
if(half) next_state = s1; //如果两个投币口,就会出现问题,一次投入可能为1.5元,所以要给输入添加约束
else of(one) next_state = s2; //文件和文件之间需要进行一些约束
else next_state = S0;
end
s1:begin
if(half) next_state = s2;
else of(one) next_state = s3;
else next_state = S1;
end
s2:begin
if(half) next_state = s3;
else of(one) next_state = s4;
else next_state = S2;
end
s3:begin
if(half) next_state = s4;
else of(one) next_state = s0;
else next_state = S3;
end
s4:begin
if(half) next_state = s0;
else of(one) next_state = s0;
else next_state = S4;
end
default: next_state = s0;
endcase
end
//第三段,写出输出
assign out = ((curr_state == s4) & (half | one)) ? 1:
((curr_state == s3) & (one)) ? 1 : 0;
assign cout = (curr_state == s4) & (one) ? 1 : 0;
endmodule
FSM有限状态机的设计步骤
- 接口定义(信号\位宽\约束)
- 状态定义和编码
- 状态转换图
- 按照三段式风格实现RTL代码
- 编写Testbench
- 使用QuestaSim进行编译和仿真
- 通过波形工具查看激励\状态信号和输出信号
- Moore机输出只与当前状态有关
- Mealy输出不仅与当前的状态有关,还与当前的输入有关


状态机的电路逻辑图
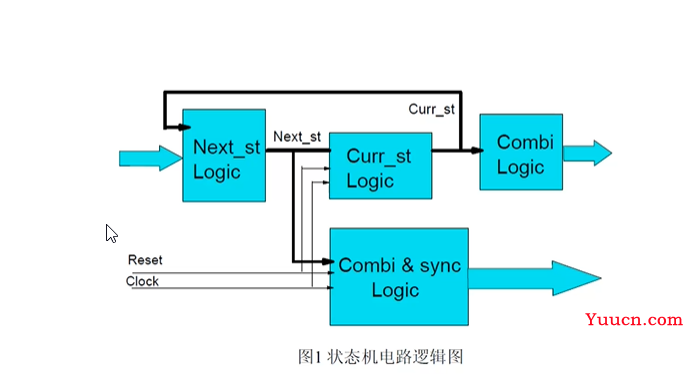
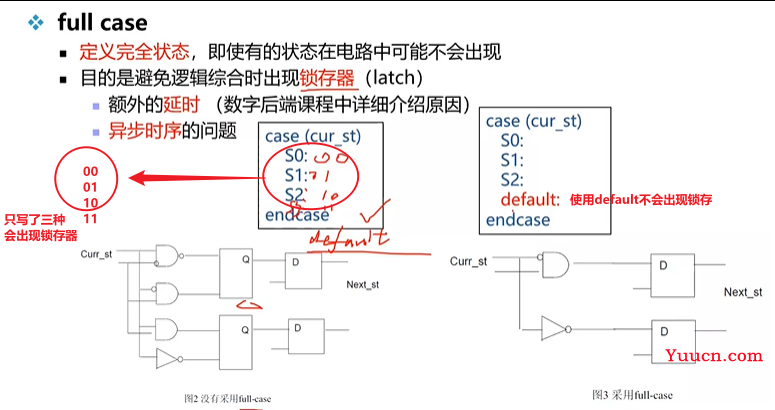
FSM要注意的问题
- case语句,要将所有的case列全
- 使用default语句还原状态;如果不写default,就需要写够所有可能
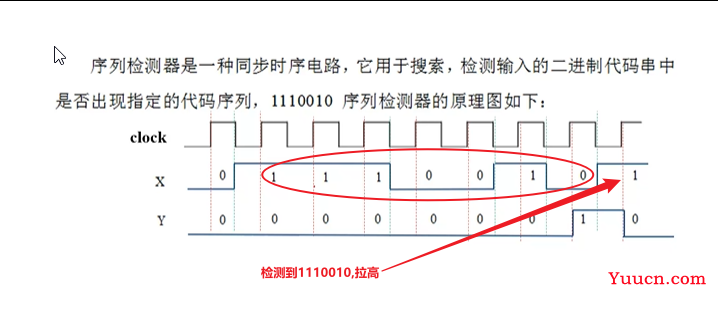
序列检测器

- 输入就是1bit的x,输出的y也是1bity
- 定义当前的状态,存储之前存储的序列是怎样的状态,初始为IDLE,中间状态可能会出现中间状态
- IDLE在定义的时候,检测的序列是从1开始的,IDLE可以直接设计为初始值为1,中间状态出现01,10等不对的状态,可以取消掉


module seq(in,out,clk,reset,state);
input in;
input clk;
input reset;
output out;
output [2:0] state;
reg [2:0] curr_state;
reg [2:0] next_state;
parameter [2:0] s0 = 3'b000,
s1 = 3'b001,
s2 = 3'b010,
s3 = 3'b011,
s4 = 3'b100,
s5 = 3'b101,
s6 = 3'b110,
s7 = 3'b111;
// 定义寄存器
always @ (posedge clk , negedge reset)
begin
if(~reset)
curr_state <= S0;
else
curr_state <= next_state;
end
// 写状态转移
always @ (in,curr_state)
begin
case(curr_state)
s0 : begin
if(in == 0) next_state <= s0;
else next_state <= s1;
end
s1 : begin
if(in == 0) next_state <= s0;
else next_state <= s2;
end
s2 : begin
if(in == 0) next_state <= s0;
else next_state <= s3;
end
s3 : begin
if(in == 0) next_state <= s4;
else next_state <= s3;
end
s4 : begin
if(in == 0) next_state <= s5;
else next_state <= s1;
end
s5 : begin
if(in == 0) next_state <= s0;
else next_state <= s6;
end
s6 : begin
if(in == 0) next_state <= s7;
else next_state <= s2;
end
s7 : begin
if(in == 0) next_state <= s0;
else next_state <= s1;
end
default: next_state <= s0;
endcase
end
// 输出
assign out = (curr_state == s7) ? 1 : 0 ;
endmodule