一、什么是深度优先遍历（DFS）
以“深度”为第一关键词，每次都沿路径到不能再前进时，才退回到最近的岔路口，然后继续按同样的逻辑搜索。
二、题目与解答
题目：
Leetcode 695.岛屿的最大面积
解答思路：
首先要遍历数组，当发现（i,j）对应为陆地时，进行如下步骤：
（1）递归解法
递归解法最重要的是首先要确定递归边界。
该题有两个递归边界：
一个是矩阵尺寸限制，
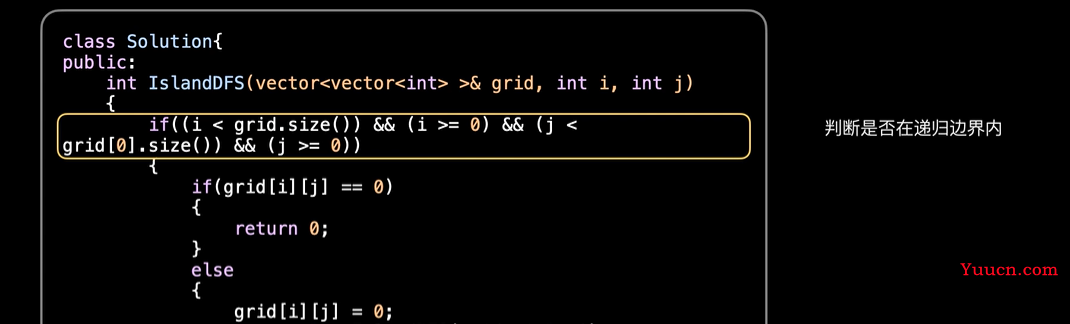
一个是碰到了水域
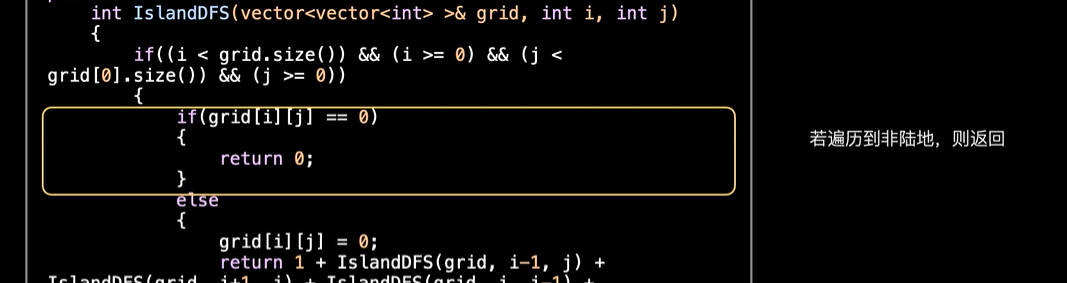
一般来说，深度优先搜索类型的题可以分为主函数和辅函数，
主函数用于遍历所有的搜索位置，判断是否可以开始搜索，如果可以即在辅函数进行搜索。
辅函数则负责深度优先搜索的递归调用
本题中主函数为：int maxAreaOfIsland(vector<vector<int>>& grid);
辅函数为：int LandDFS(vector<vector<int>>& grid, int i, int j); 其中i, j 代表当前坐标。
class Solution {
public:
// 辅函数
int LandDFS(vector<vector<int>>& grid, int i, int j)
{
// 在矩阵尺寸范围内
if((i < grid.size()) && (i >= 0) && (j < grid[0].size()) && (j >= 0)) {
if (grid[i][j] == 0) { // 碰到水
return 0;
}
else {
grid[i][j] = 0;
return 1 + LandDFS(grid, i-1, j) + LandDFS(grid, i+1, j) +
LandDFS(grid, i, j-1) + LandDFS(grid, i, j+1);
}
}
else {
return 0;
}
}
// 主函数
int maxAreaOfIsland(vector<vector<int>>& grid) {
int ans = 0;
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[0].size(); j++) {
ans = max(ans, LandDFS(grid, i, j)); // 这里LandDFS(grid, i, j)返回的是含(i,j)的岛屿的面积
}
}
return ans;
}
};
（2）栈解法
我们也可以使用栈（stack）实现深度优先搜索，但因为栈与递归的调用原理相同，而递归相对便于实现，因此刷题时推荐使用递归式写法，同时也方便进行回溯（见下节）。
不过在实际工程上，直接使用栈可能才是最好的选择，一是因为便于理解，二是更不易出现递归栈满的情况。
class Solution {
private:
vector<int> direction {-1, 0, 1, 0, -1}; // 每相邻两位即为上下左右四个方向之一
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int localArea, area = 0, x, y;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j]) { // 进入岛屿
localArea = 1;
grid[i][j] = 0; // 抹除
stack<pair<int, int>> IsLand; // 存放土地的堆栈
IsLand.push({i, j}); // 往堆中加入当前土地（该岛第一块土地）
while (!IsLand.empty()) {
auto [r, c] = IsLand.top(); // 从堆中取出元素，并访问
IsLand.pop(); // 从堆中取出元素，并访问
for (int k = 0; k < 4; k++) { // 上下左右
x = r + direction[k];
y = c + direction[k+1];
if ( x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
++localArea;
grid[x][y] = 0;
IsLand.push({x, y}); // 往堆中加入当前土地 ( (i,j)土地的领接土地节点 )
}
}
}
}
area = max(area, localArea);
}
}
return area;
}
};
参考视频：
https://leetcode.cn/problems/max-area-of-island/solution/dao-yu-de-zui-da-mian-ji-by-leetcode-solution/
声明：本站所有文章，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。
评论(0)