笔者最近用FPGA实现的64点IFFT,记录一下作为笔记也可以为各位读者提供一个思路。(输入12bit实数+12bit虚数)
IFFT算法的原理这里就不再赘述,主要讲解算法的实现过程。
如图2:我们要用FPGA实现此算法的话,利用流水线的思想,可分为如下几步:1.输入重新排序。2.对应数据与蝶形算子相乘。3.将复乘结果与对应数据相加/减得到输出。4.输出作为输入参与下一级运算直到最后一级。
1.输入排序:如下面图1和图2所示,输入序列的顺序就是自然序的二进制的倒序对应的十进制数。
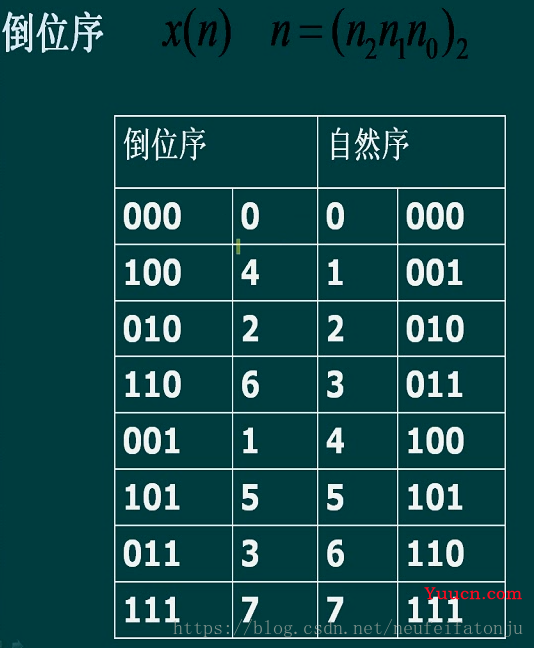
图1
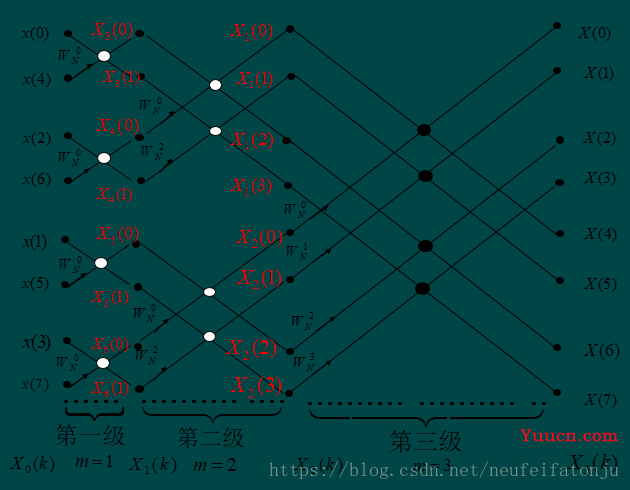
图2
2.复乘运算:复乘运算的对象是每一级的输入数据与旋转因子。旋转因子实际的值是实部虚部都不大于1的复数,如果不对旋转因子进行放大就去参与复乘运算需要浮点运算,而fpga实现浮点运算特别消耗资源,所以这里我将旋转因子×2^10后变成12bit复数与对应的每一级输入进行复乘运算。运算工具用vivado自带的Complex Multiplier IP核。
注:因为 在运算前将旋转因子×2^10,对于复乘后的结果要右移十位。此外,我们可以根据结果适当删去不需要的位数。例如这里的复乘是实虚12bit数据×实虚12bit旋转因子,本来复乘需要乘法和加法两次运算,而每次运算导致结果都会增加1bit,但在这里扩大后的旋转因子最大只有2^10,与数据相乘后的最大值并不达到要扩充位数的标准,所以这里的复乘运算的结果是实部虚部都是13bit的复数,于是我们可以对Complex Multiplier IP核输出的结果进行截位以减少资源消耗。
3.加/减法运算:将复乘后的结果与对应输入相加/减得出这一级的输出。
4.下一级重复上述操作直到最后一级。
附:对于批量编辑代码的问题,我们可以利用matlab提供的交互式操作方式去产生我们想要的结果复制后利用在文本编辑器的列模式下粘贴。