文章目录
- 参考资料
- 1. 以车辆重心为中心的单车运动学模型
-
- 1.1 参数说明
- 1.2 几何关系
-
- 1.2.1 偏航角
ψ
\psi
ψ的关系 - 1.2.1 滑移角
β
\beta
β 的关系 - 1.2.2 运动学模型
- 1.2.1 偏航角
- 1.3 python 实现
- 2. 以前轮驱动的单车运动学模型
-
- 2.1 几何关系
- 2.2 python实现
- 3. 以后轴中心为车辆中心的单车运动学模型
-
- 3.1 几何关系
- 3.2 python实现
- 4. 阿克曼转向几何
参考资料
- 自动驾驶中的车辆运动学模型
- 车辆数学模型
- 车辆运动学模型
- 车辆控制-运动学模型(Kinematic Model)
- 运动学模型及其线性化
模型的用处就是在当前状态给定某控制输入时,预测(估计) 系统未来的状态。控制领域利用模型设计合适的输入,以期控制系统到达目标状态。
1. 以车辆重心为中心的单车运动学模型
1.1 参数说明
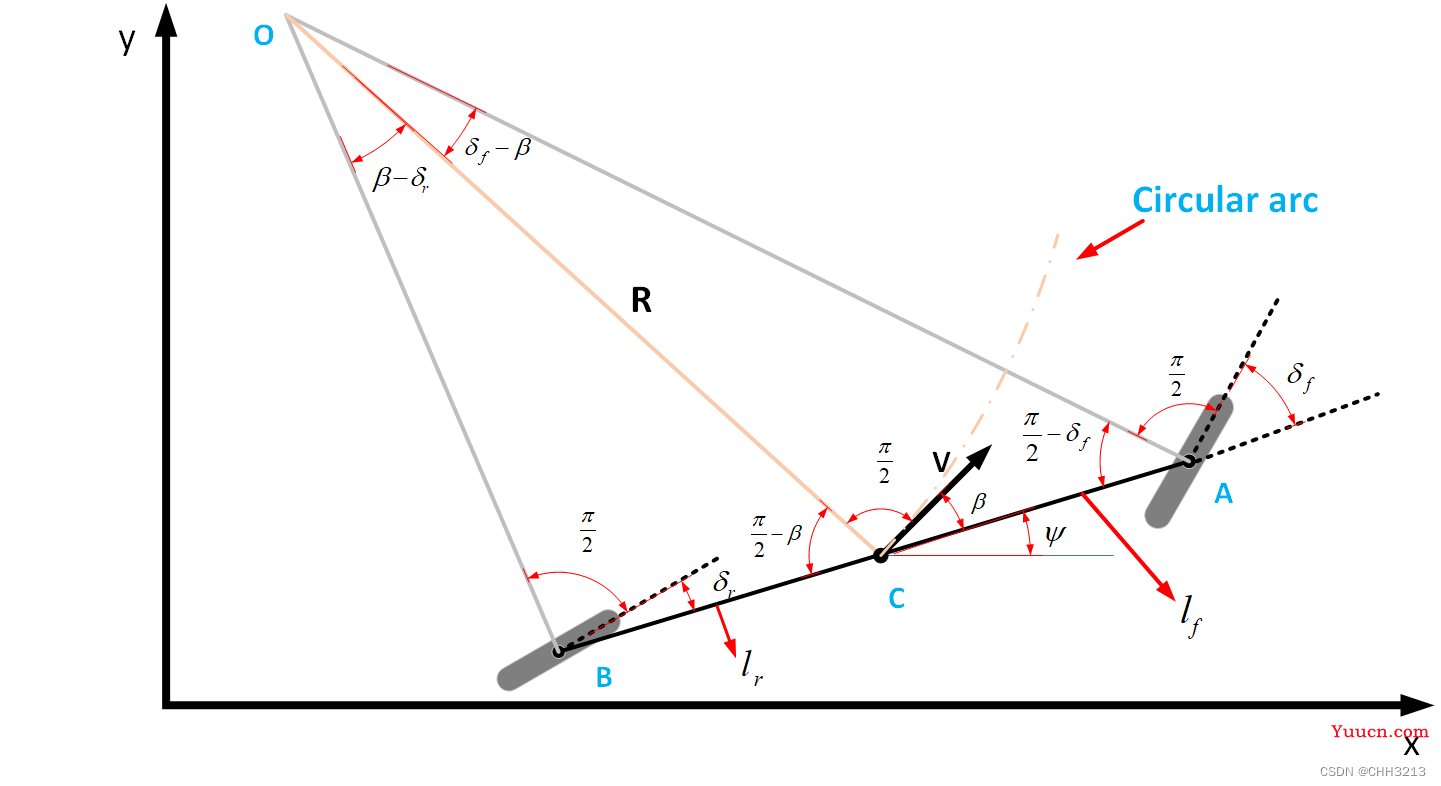
一般考虑运动学模型时,将车辆模型简化成单车模型(bicycle model)。
单车模型中:
-
左右轮等效为单个轮子
左右前轮合并为单个轮子,其中心点为A点,同样后轮等效后的中心点为 B点。 -
转向角
前后轮的转向角用
δ
f
\delta_f
δf和
δ
r
\delta_r
δr表示,模型中前后轮都可以转向,对于只有前轮转向的系统,后轮转向角
δ
r
\delta_r
δr可以设置为0. -
重心
点 C 代表车辆的重心, A 点和 B点到重心的距离分别用
l
f
l_f
lf和
l
r
l_r
lr表示,轴距表示为
L
=
l
f
+
l
r
L = l_f + l_r
L=lf+lr。 -
速度
车辆重心的速度用
V
V
V表示,与车辆纵向轴的夹角为
β
\beta
β,该角度叫做车辆的滑移角。 -
运动描述
假设车辆平动,车辆运动状态可以用三个坐标量描述:
x
x
x 、
y
y
y 和
ψ
\psi
ψ。其中
(
x
,
y
)
(x,y)
(x,y)代表车辆的位置,
ψ
\psi
ψ描述的是航向角(Heading Angle),指车身与X轴的夹角。 -
条件假设
假设速度矢量
V
V
V的方向在点
A
A
A点和
B
B
B点的方向与转向角的方向相同,换句话说,在A点的速度矢量与车辆纵轴的夹角为
δ
f
\delta_f
δf,同样
B
B
B点的速度矢量与车辆纵轴的夹角为
δ
r
\delta_r
δr。也就是说前后轮的滑移角
β
\beta
β都为0。该条件假设成立前提的是车辆速度很低(<5m/s),此时轮胎产生的横向力很小,可以忽略。 -
轨迹半径
点
O
O
O代表车辆的瞬时旋转中心,线段
A
O
AO
AO与
B
O
BO
BO与前后两个转轮方向垂直,他们的交点即为
O
O
O点,线段
O
C
OC
OC的长度代表车辆的轨迹半径
R
R
R。 -
航迹角
车辆重心处的速度垂直于
O
C
OC
OC,车辆速度矢量与车辆纵轴的夹角为
β
\beta
β,车辆的航向角为
ψ
\psi
ψ,则航迹角为
γ
=
ψ
+
β
\gamma = \psi + \beta
γ=ψ+β。
1.2 几何关系
1.2.1 偏航角
ψ
\psi
ψ的关系
如上图所示,在三角形
O
C
A
OCA
OCA中,根据正弦定理,有:
sin
(
δ
f
−
β
)
l
f
=
sin
(
π
2
−
δ
f
)
R
(1)
\tag{1} \frac{\sin \left(\delta_{f}-\beta\right)}{l_{f}}=\frac{\sin \left(\frac{\pi}{2}-\delta_{f}\right)}{R}
lfsin(δf−β)=Rsin(2π−δf)(1)
在三角形
O
B
C
OBC
OBC中,根据正弦定理,有:
sin
(
β
−
δ
r
)
l
r
=
sin
(
π
2
+
δ
r
)
R
(2)
\tag{2} \frac{\sin \left(\beta-\delta_{r}\right)}{l_{r}}=\frac{\sin \left(\frac{\pi}{2}+\delta_{r}\right)}{R}
lrsin(β−δr)=Rsin(2π+δr)(2)
展开公式(1)(2)可得:
sin
δ
f
cos
β
−
sin
β
cos
δ
f
l
f
=
cos
δ
f
R
(3)
\tag{3} \frac{\sin \delta_{f} \cos \beta-\sin \beta \cos \delta_{f}}{l_{f}}=\frac{\cos \delta_{f}}{R}
lfsinδfcosβ−sinβcosδf=Rcosδf(3)
sin
β
cos
δ
r
−
cos
β
sin
δ
r
l
r
=
cos
δ
r
R
(4)
\tag{4} \frac{\sin \beta\cos \delta_{r} -\cos \beta \sin \delta_{r}}{l_{r}}=\frac{\cos \delta_{r}}{R}
lrsinβcosδr−cosβsinδr=Rcosδr(4)
等式(3)两边同时乘
l
f
cos
(
δ
f
)
\frac{l_{f}}{\cos \left(\delta_{f}\right)}
cos(δf)lf 得
tan
(
δ
f
)
cos
(
β
)
−
sin
(
β
)
=
l
f
R
(5)
\tag{5} \tan \left(\delta_{f}\right) \cos (\beta)-\sin (\beta)=\frac{l_{f}}{R}
tan(δf)cos(β)−sin(β)=Rlf(5)
同理,等式(4)两边同时乘
l
r
cos
(
δ
r
)
\frac{l_{r}}{\cos \left(\delta_{r}\right)}
cos(δr)lr 得
sin
(
β
)
−
tan
(
δ
r
)
cos
(
β
)
=
l
r
R
(6)
\tag{6} \sin (\beta)-\tan \left(\delta_{r}\right) \cos (\beta)=\frac{l_{r}}{R}
sin(β)−tan(δr)cos(β)=Rlr(6)
联立公式(5)(6)可得:
(
tan
δ
f
−
tan
δ
r
)
cos
β
=
l
f
+
l
r
R
(7)
\tag{7} \left(\tan \delta_{f}-\tan \delta_{r}\right) \cos \beta=\frac{l_{f}+l_{r}}{R}
(tanδf−tanδr)cosβ=Rlf+lr(7)
根据条件假设,低速环境下,车辆行驶路径的转弯半径变化缓慢,此时我们可以假设车辆偏航角的变化率率
ψ
˙
\dot{\psi}
ψ˙可近似等于车辆的角速度
ω
\omega
ω。根据车辆角速度
ω
=
V
R
\omega = \frac{V}{R}
ω=RV得
ψ
˙
=
V
R
(8)
\tag{8} \dot{\psi}=\frac{V}{R}
ψ˙=RV(8)
将公式(8)带入公式(7)中,消除
R
R
R项得
ψ
˙
=
V
cos
β
l
f
+
l
r
(
tan
δ
f
−
tan
δ
r
)
(9)
\tag{9} \dot{\psi}=\frac{V \cos \beta}{l_{f}+l_{r}}\left(\tan \delta_{f}-\tan \delta_{r}\right)
ψ˙=lf+lrVcosβ(tanδf−tanδr)(9)
1.2.1 滑移角
β
\beta
β 的关系
等式(5)乘以
l
r
l_{r}
lr 得
tan
(
δ
f
)
cos
(
β
)
l
r
−
sin
(
β
)
l
r
=
l
f
⋅
l
r
R
(10)
\tag{10} \tan \left(\delta_{f}\right) \cos (\beta) l_{r}-\sin (\beta) l_{r}=\frac{l_{f} \cdot l_{r}}{R}
tan(δf)cos(β)lr−sin(β)lr=Rlf⋅lr(10)
等式(6)乘以
l
f
l_{f}
lf 得
sin
(
β
)
l
f
−
tan
(
δ
r
)
cos
(
β
)
l
f
=
l
f
⋅
l
r
R
(11)
\tag{11} \sin (\beta) l_{f}-\tan \left(\delta_{r}\right) \cos (\beta) l_{f}=\frac{l_{f} \cdot l_{r}}{R}
sin(β)lf−tan(δr)cos(β)lf=Rlf⋅lr(11)
等式(10)和(11)相减得
cos
(
β
)
(
l
f
tan
(
δ
r
)
+
l
r
tan
(
δ
f
)
)
=
sin
(
β
)
(
l
f
+
l
r
)
(12)
\tag{12} \cos (\beta)\left(l_{f} \tan \left(\delta_{r}\right)+l_{r} \tan \left(\delta_{f}\right)\right)=\sin (\beta)\left(l_{f}+l_{r}\right)
cos(β)(lftan(δr)+lrtan(δf))=sin(β)(lf+lr)(12)
等式(12)两端同时乘以
1
cos
(
β
)
\frac{1}{\cos (\beta)}
cos(β)1 得
tan
(
β
)
=
l
f
tan
(
δ
r
)
+
l
r
tan
(
δ
f
)
l
f
+
l
r
(13)
\tag{13} \tan (\beta)=\frac{l_{f} \tan \left(\delta_{r}\right)+l_{r} \tan \left(\delta_{f}\right)}{l_{f}+l_{r}}
tan(β)=lf+lrlftan(δr)+lrtan(δf)(13)
故取反三角函数得
β
=
arctan
(
l
f
tan
(
δ
r
)
+
l
r
tan
(
δ
f
)
l
f
+
l
r
)
(14)
\tag{14} \beta=\arctan \left(\frac{l_{f} \tan \left(\delta_{r}\right)+l_{r} \tan \left(\delta_{f}\right)}{l_{f}+l_{r}}\right)
β=arctan(lf+lrlftan(δr)+lrtan(δf))(14)
1.2.2 运动学模型
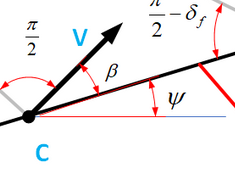
根据上图,很容易得到
x
,
y
x,y
x,y方向的速度为
x
˙
=
V
cos
(
β
+
ψ
)
y
˙
=
V
sin
(
β
+
ψ
)
(15)
\tag{15} \begin{aligned} &\dot{x}=V \cos (\beta+\psi)\\ &\dot{y}=V \sin (\beta+\psi) \end{aligned}
x˙=Vcos(β+ψ)y˙=Vsin(β+ψ)(15)
综上,以车辆重心为中心的运动学模型为
{
x
˙
=
V
cos
(
ψ
+
β
)
y
˙
=
V
sin
(
ψ
+
β
)
ψ
˙
=
V
cos
β
l
f
+
l
r
(
tan
δ
f
−
tan
δ
r
)
(16)
\tag{16} \left\{\begin{array}{l} \dot{x}=V \cos (\psi+\beta) \\ \dot{y}=V \sin (\psi+\beta) \\ \dot{\psi}=\frac{V \cos \beta}{l_{f}+l_{r}}\left(\tan \delta_{f}-\tan \delta_{r}\right)\\ \end{array}\right.
⎩⎨⎧x˙=Vcos(ψ+β)y˙=Vsin(ψ+β)ψ˙=lf+lrVcosβ(tanδf−tanδr)(16)
其中,
β
=
arctan
(
l
f
tan
(
δ
r
)
+
l
r
tan
(
δ
f
)
l
f
+
l
r
)
\beta=\arctan \left(\frac{l_{f} \tan \left(\delta_{r}\right)+l_{r} \tan \left(\delta_{f}\right)}{l_{f}+l_{r}}\right)
β=arctan(lf+lrlftan(δr)+lrtan(δf))
1.3 python 实现
class KinematicModel_1:
"""假设控制量为前后轮的转向角delta_f,delta_r和加速度a
"""
def __init__(self, x, y, psi, v, l_r, l_f, dt):
self.x = x
self.y = y
self.psi = psi
self.v = v
self.l_f = l_f
self.l_r = l_r
# 实现是离散的模型
self.dt = dt
def update_state(self, a, delta_f,delta_r):
beta = math.atan((self.l_r*math.tan(delta_f)+self.l_f*math.tan(delta_r))/(self.l_f+self.l_r))
self.x = self.x+self.v*math.cos(self.psi+beta)*self.dt
self.y = self.y+self.v*math.sin(self.psi+beta)*self.dt
self.psi = self.psi+self.v*math.cos(beta)*(math.tan(delta_f)-math.tan(delta_r))/(self.l_f+self.l_r)*self.dt
self.v = self.v+a*self.dt
def get_state(self):
return self.x, self.y, self.psi, self.v
2. 以前轮驱动的单车运动学模型
2.1 几何关系
由于绝大多数的汽车后轮都不能够偏转,所以在单车模型基础上,我们假定后轮的转角控制输入
δ
r
=
\delta_r=0
δr=0,即车辆为前轮驱动(front−wheel−only)。也就是说,方向盘上的控制输入,都反映到了前轮的转角上了,即认为方向盘的转角就等于前轮的转角
δ
f
\delta_f
δf。
注意:这里依旧以车辆重心为中心。
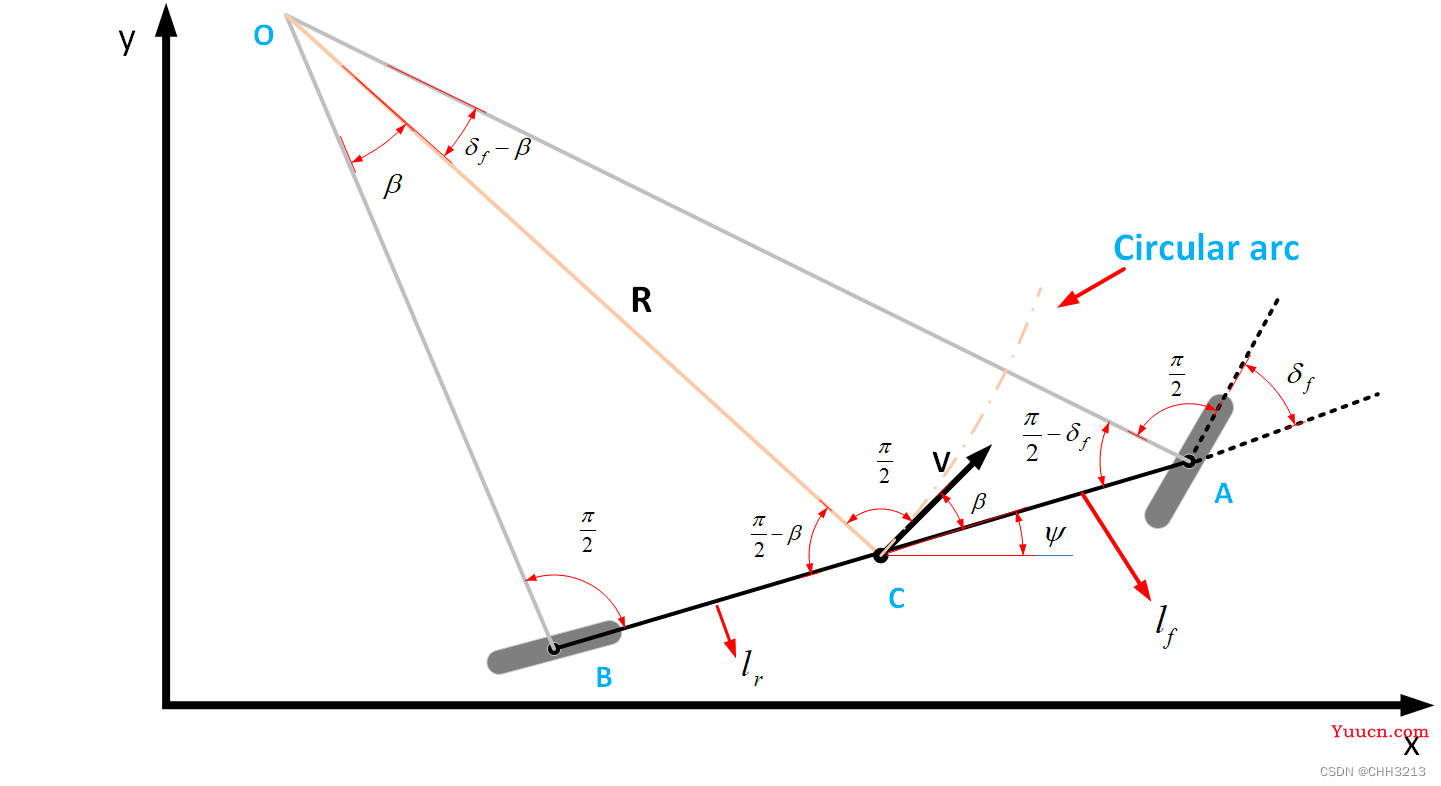
在直角三角形
O
B
C
OBC
OBC中,易得
sin
β
=
l
r
R
(17)
\tag{17} \sin{\beta}=\frac{l_r}{R}
sinβ=Rlr(17)
将公式(8)代入公式(17)得
ψ
˙
=
V
sin
β
l
r
(18)
\tag{18} \dot{\psi}=\frac{V \sin{\beta}}{l_r}
ψ˙=lrVsinβ(18)
故前轮驱动的车辆运动学模型为
{
x
˙
=
V
cos
(
ψ
+
β
)
y
˙
=
V
sin
(
ψ
+
β
)
ψ
˙
=
V
sin
β
l
r
(19)
\tag{19} \left\{\begin{array}{l} \dot{x}=V \cos (\psi+\beta) \\ \dot{y}=V \sin (\psi+\beta) \\\dot{\psi}=\frac{V \sin{\beta}}{l_r} \end{array}\right.
⎩⎨⎧x˙=Vcos(ψ+β)y˙=Vsin(ψ+β)ψ˙=lrVsinβ(19)
其中,
β
\beta
β的推导方式与前文一致(可直接令公式(14)的
δ
r
=
\delta_r=0
δr=0),可得
β
=
arctan
(
l
r
l
f
+
l
r
tan
(
δ
f
)
)
(20)
\tag{20} \beta=\arctan \left(\frac{l_{r} }{l_{f}+l_{r}}\tan \left(\delta_{f}\right)\right)
β=arctan(lf+lrlrtan(δf))(20)
2.2 python实现
class KinematicModel_2:
"""假设控制量为前轮的转向角delta_f和加速度a
"""
def __init__(self, x, y, psi,v,l_r,l_f,dt):
self.x = x
self.y = y
self.psi = psi
self.v = v
self.l_f = l_f
self.l_r = l_r
# 实现是离散的模型
self.dt=dt
def update_state(self,a,delta_f):
beta = math.atan((self.l_r)/(self.l_f+self.l_r)*math.tan(delta_f))
self.x = self.x+self.v*math.cos(self.psi+beta)*self.dt
self.y = self.y+self.v*math.sin(self.psi+beta)*self.dt
self.psi = self.psi+self.v*math.sin(beta)/self.l_r*self.dt
self.v = self.v+a*self.dt
def get_state(self):
return self.x, self.y, self.psi, self.v
3. 以后轴中心为车辆中心的单车运动学模型
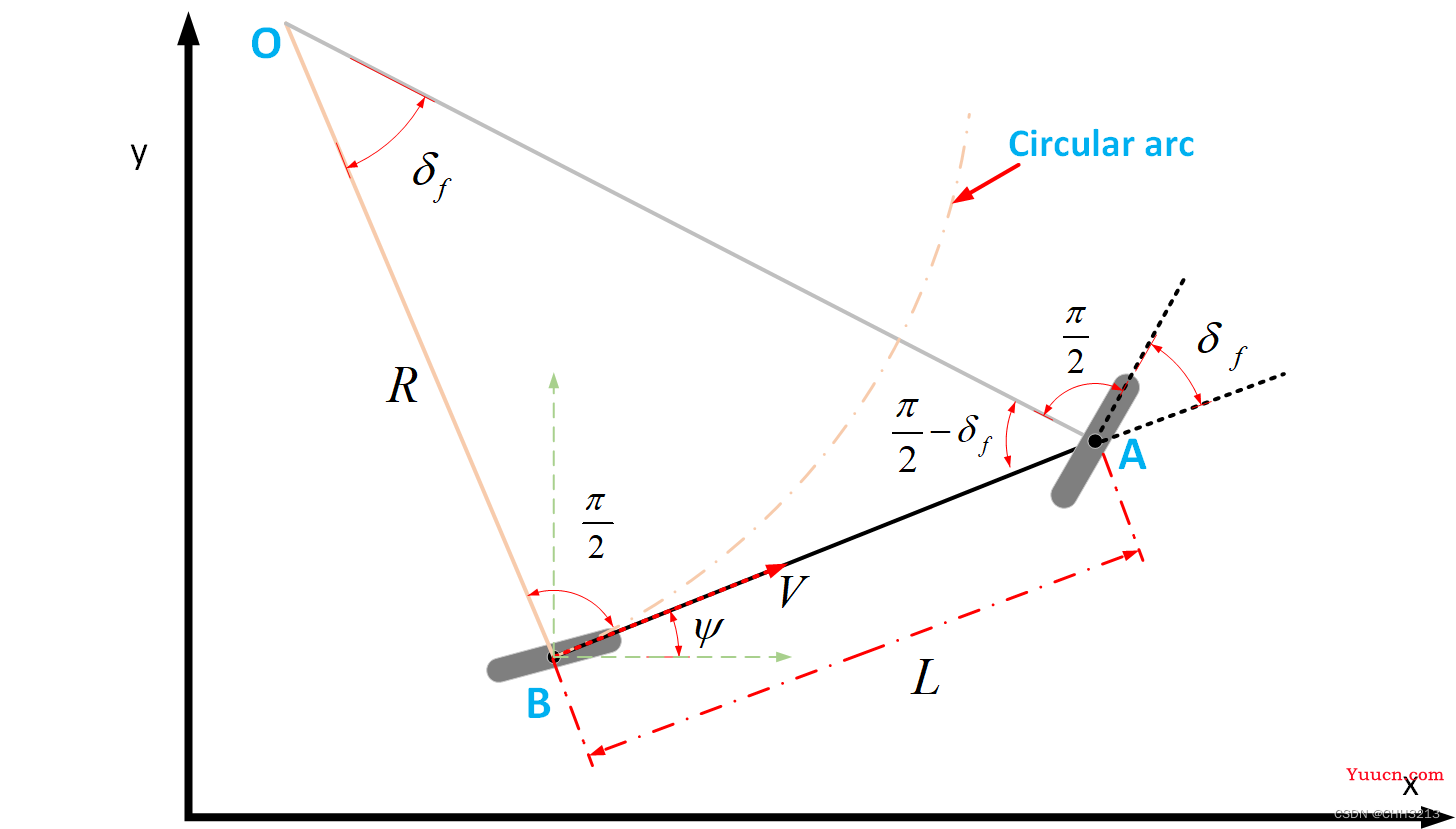
3.1 几何关系
在直角三角形
O
B
A
OBA
OBA中,显然有
tan
δ
f
=
L
R
(21)
\tag{21} \tan{\delta_f}=\frac{L}{R}
tanδf=RL(21)
联立公式(7),可得:
ψ
˙
=
V
L
tan
δ
f
\dot{\psi}=\frac{V}{L}\tan{\delta_f}
ψ˙=LVtanδf
另外,根据几何关系,显然有
x
˙
=
V
cos
(
ψ
)
y
˙
=
V
sin
(
ψ
)
\dot{x}=V \cos (\psi) \\ \dot{y}=V \sin (\psi)
x˙=Vcos(ψ)y˙=Vsin(ψ)
因此,以后轴中心为车辆中心的运动学模型为
{
x
˙
=
V
cos
(
ψ
)
y
˙
=
V
sin
(
ψ
)
ψ
˙
=
V
L
tan
δ
f
(22)
\tag{22} \left\{\begin{array}{l} \dot{x}=V \cos (\psi) \\ \dot{y}=V \sin (\psi) \\ \dot{\psi}=\frac{V}{L}\tan{\delta_f} \end{array}\right.
⎩⎨⎧x˙=Vcos(ψ)y˙=Vsin(ψ)ψ˙=LVtanδf(22)
如果使用车辆的加速度
a
a
a作为 控制,则再加上下面这个公式即可
V
˙
=
a
(23)
\tag{23} \dot{V}=a
V˙=a(23)
但在无人车控制过程中,一般控制对象
u
=
[
v
,
w
]
T
u=\left[v, w\right]^{T}
u=[v,w]T ,则式(22)可写为:
[
x
˙
y
˙
ψ
˙
]
=
[
cos
ψ
sin
ψ
]
v
+
[
1
]
w
\left[\begin{array}{c} \dot{x}\\ \dot{y} \\ \dot{\psi} \end{array}\right]=\left[\begin{array}{c} \cos \psi \\ \sin \psi \\ 0 \end{array}\right] v+\left[\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right] w
⎣⎡x˙y˙ψ˙⎦⎤=⎣⎡cosψsinψ0⎦⎤v+⎣⎡001⎦⎤w
速度
v
v
v 的控制主要通过刹车 (brake) 、油门 (throttle) 、档位 (gear) 等来控制,横摆角速度
w
w
w主要通过转动方向盘 (steer) 来 控制。
3.2 python实现
class KinematicModel_3:
"""假设控制量为转向角delta_f和加速度a
"""
def __init__(self, x, y, psi,v,L,dt):
self.x = x
self.y = y
self.psi = psi
self.v = v
self.L = L
# 实现是离散的模型
self.dt=dt
def update_state(self,a,delta_f):
self.x = self.x+self.v*math.cos(self.psi)*self.dt
self.y = self.y+self.v*math.sin(self.psi)*self.dt
self.psi = self.psi+self.v/self.L*math.tan(delta_f)*self.dt
self.v = self.v+a*self.dt
def get_state(self):
return self.x, self.y, self.psi, self.v
所有实现代码欢迎访问我的github仓库,正在持续更新中~~
4. 阿克曼转向几何
汽车采用阿克曼转向轮。阿克曼转向几何(Ackerman Turning Geometry)是一种为了解决交通工具转弯时,内外转向轮路径指向的圆心不同的几何学。
在单车模型中,将转向时左、右前轮偏角假设为同一角度
δ
f
\delta_f
δf,虽然通常两个角度大致相等,但实际并不是,通常情况下,内侧轮胎转角更大。如下图所示。
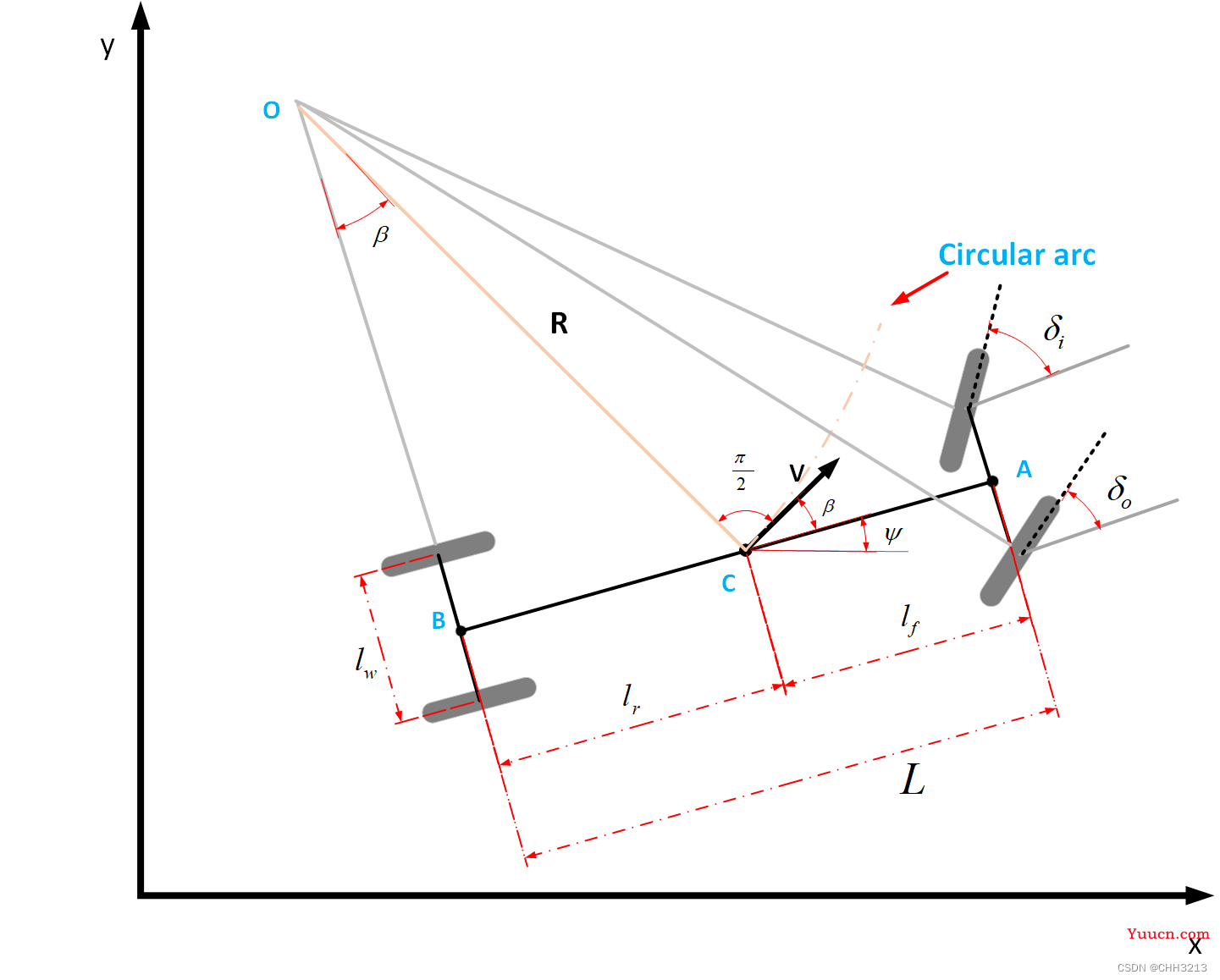
δ
o
\delta_{o}
δo 和
δ
i
\delta_{i}
δi 分别为外侧前轮和内侧前轮偏角,当车辆左转时,左前轮胎为内侧轮胎,其转角
δ
i
\delta_{i}
δi 较 右前轮胎转角
δ
o
\delta_{o}
δo 更大。
l
w
l_{w}
lw 为轮距,
L
=
l
f
+
l
r
L=l_f+l_r
L=lf+lr 为轴距,远远小于轨迹半径
R
R
R,滑移角
β
\beta
β接近于0。一般车辆模型后轴为固定轴,故后轮两轮胎转角为
∘
0^{\circ}
0∘,即
δ
r
\delta_r
δr为0 。
当以后轴中心为参考点时,则
O
B
OB
OB为转向半径R。
当滑移角
β
\beta
β很小时,且后轮偏角为0时,公式(9)可近似为
ψ
˙
≈
V
L
tan
(
δ
f
)
(24)
\tag{24} \dot{\psi}\approx \frac{V}{L} \tan \left(\delta_{f}\right)
ψ˙≈LVtan(δf)(24)
由于
δ
f
\delta_{f}
δf 很小
tan
(
δ
f
)
≈
δ
f
(25)
\tag{25} \tan \left(\delta_{f}\right) \approx \delta_{f}
tan(δf)≈δf(25)
根据公式(8)和公式(24)得
ψ
˙
V
≈
δ
f
L
=
1
R
(26)
\tag{26} \frac{\dot{\psi}}{V} \approx \frac{\delta_{f}}{L}=\frac{1}{R}
Vψ˙≈Lδf=R1(26)
故不区分前后轴,等效转向角为
δ
=
L
R
(27)
\tag{27} \delta=\frac{L}{R}
δ=RL(27)
由于内外轮的转弯半径不同,根据公式(27), 外轮转角为
δ
o
=
L
R
+
l
w
2
(28)
\tag{28} \delta_{o}=\frac{L}{R+\frac{l_{w}}{2}}
δo=R+2lwL(28)
内轮转角为
δ
i
=
L
R
−
l
w
2
(29)
\tag{29} \delta_{i}=\frac{L}{R-\frac{l_{w}}{2}}
δi=R−2lwL(29)
故前轮平均转向角为
δ
=
δ
o
+
δ
i
2
=
L
R
−
l
w
2
4
R
(30)
\tag{30} \delta=\frac{\delta_{o}+\delta_{i}}{2}=\frac{L}{R-\frac{l_{w}^{2}}{4 R}}
δ=2δo+δi=R−4Rlw2L(30)
由于
l
w
2
4
R
\frac{l_{w}^{2}}{4 R}
4Rlw2 项中,
l
w
l_{w}
lw 远远小于
R
R
R, 且
l
w
l_{w}
lw 的二次项更小,故
l
w
2
4
R
≅
(31)
\tag{31} \frac{l_{w}^{2}}{4 R} \cong 0
4Rlw2≅0(31)
所以等式(30)可以近似为
δ
=
L
R
(32)
\tag{32} \delta=\frac{L}{R}
δ=RL(32)
比较等式(28)和(29)知,
δ
i
\delta_{i}
δi 始终大于
δ
o
\delta_{o}
δo ,故
δ
i
−
δ
o
=
L
R
−
l
w
2
−
L
R
+
l
w
2
=
L
l
w
R
2
−
l
w
2
4
≅
L
R
2
l
w
=
δ
2
l
w
L
(33)
\tag{33} \begin{aligned} \delta_{i}-\delta_{o} &=\frac{L}{R-\frac{l_{w}}{2}}-\frac{L}{R+\frac{l_{w}}{2}} \\ &=\frac{L l_{w}}{R^{2}-\frac{l_{w}^{2}}{4}} \\ & \cong \frac{L}{R^{2}} l_{w}=\delta^{2} \frac{l_{w}}{L} \end{aligned}
δi−δo=R−2lwL−R+2lwL=R2−4lw2Llw≅R2Llw=δ2Llw(33)
根据公式(33)可知,前轮内外转向角的差值接近于平均转向角的二次方,所以当前轮转向角较大时, 内外轮的转向角误差就越大。
依据阿克曼转向几何设计的车辆,沿着弯道转弯时,利用四连杆的相等曲柄使内侧轮的转向角比外侧轮大大约2~4度,使四个轮子路径的圆心大致上交会于后轴的延长线上瞬时转向中心,让车辆可以顺畅的转弯。
车辆运动模型基于单车模型推导,推导过程不考虑车辆受到的横向力,故该模型只适用于车辆速度很低的情形。
a
=
m
V
2
R
(34)
\tag{34} a=\frac{m V^{2}}{R}
a=RmV2(34)
根据公式(34)知,速度很小时,车辆受到的向心力可以忽略不记,所以才有公式(8)的成立。所以当车辆的运动场景速度较低时,可以使用该模型描述车辆的运动。