目标检测--边框回归损失函数SIoU原理详解及代码实现

1. SIoU

1.1 原理

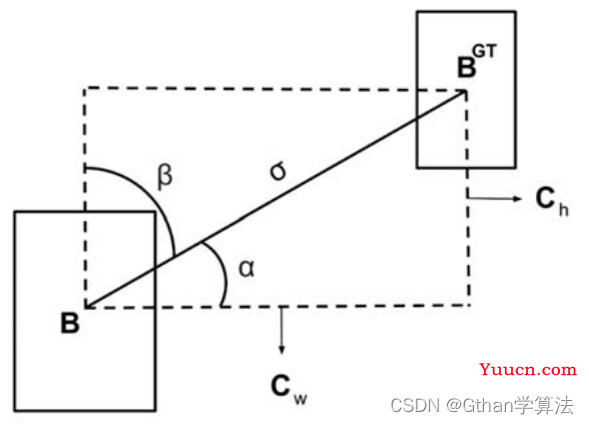
有关IoU损失函数，如(GIoU, DIoU, CIoU)没有考虑到真实框与预测框框之间的方向，导致收敛速度较慢，对此SIoU引入真实框和预测框之间的向量角度，重新定义相关损失函数，具体包含四个部分：
（1）角度损失(Angle cost)，定义如下


Λ
=
1
−
2
∗
sin
⁡
2
(
arcsin
⁡
(
c
h
σ
)
−
π
4
)
=
cos
⁡
(
2
∗
(
arcsin
⁡
(
c
h
σ
)
−
π
4
)
)
\Lambda = 1-2*\sin^2(\arcsin(\frac{c_h}{\sigma}) - \frac{\pi}{4})=\cos(2*(\arcsin(\frac{c_h}{\sigma}) - \frac{\pi}{4}))
Λ=1−2∗sin2(arcsin(σch​​)−4π​)=cos(2∗(arcsin(σch​​)−4π​))
其中
c
h
c_h
ch​为真实框和预测框中心点的高度差，$\sigma$为真实框和预测框中心点的距离，事实上
arcsin
⁡
(
c
h
σ
)
\arcsin (\frac{c_h}{\sigma})
arcsin(σch​​)等于角度$\alpha$

c
h
σ
=
sin
⁡
(
α
)
\frac{c_h}{\sigma}=\sin(\alpha)
σch​​=sin(α)

σ
=
(
b
c
x
g
t
−
b
c
x
)
2
+
(
b
c
y
g
t
−
b
c
y
)
2
\sigma = \sqrt{(b_{c_x}^{gt}-b_{c_x})^2+(b_{c_y}^{gt}-b_{c_y})^2}
σ=(bcx​gt​−bcx​​)2+(bcy​gt​−bcy​​)2​

c
h
=
max
⁡
(
b
c
y
g
t
,
b
c
y
)
−
min
⁡
(
b
c
y
g
t
,
b
c
y
)
c_h = \max(b_{c_y}^{gt}, b_{c_y}) - \min(b_{c_y}^{gt}, b_{c_y})
ch​=max(bcy​gt​,bcy​​)−min(bcy​gt​,bcy​​)

(
b
c
x
g
t
,
b
c
y
g
t
)
(b_{c_x}^{gt}, b_{c_y}^{gt})
(bcx​gt​,bcy​gt​)为真实框中心坐标
(
b
c
x
,
b
c
y
)
(b_{c_x}, b_{c_y})
(bcx​​,bcy​​)为预测框中心坐标，可以注意到当$\alpha$为
π
2
\frac{\pi}{2}
2π​或0时，角度损失为0，在训练过程中若
α
<
π
4
\alpha < \frac{\pi}{4}
α<4π​，则最小化$\alpha$，否则最小化$\beta$

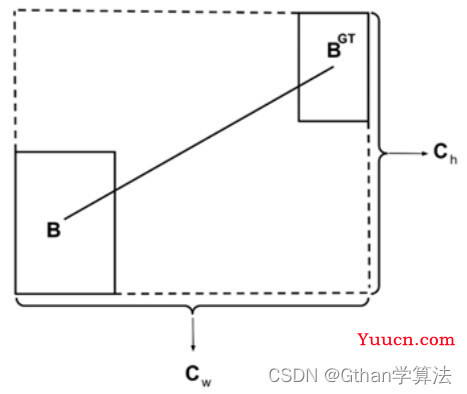
（2）距离损失(Distance cost)，定义如下：


Δ
=
∑
t
=
x
,
y
(
1
−
e
−
γ
ρ
t
)
=
2
−
e
−
γ
ρ
x
−
e
−
γ
ρ
y
\Delta = \sum_{t=x,y}(1-e^{-\gamma\rho_t})=2-e^{-\gamma\rho_x}-e^{-\gamma\rho_y}
Δ=t=x,y∑​(1−e−γρt​)=2−e−γρx​−e−γρy​
其中：

ρ
x
=
(
b
c
x
g
t
−
b
c
x
c
w
)
2
,
ρ
y
=
(
b
c
y
g
t
−
b
c
y
c
h
)
2
γ
=
2
−
Λ
\rho_x = (\frac{b_{c_x}^{gt} - b_{c_x}}{c_w})^2, \quad \rho_y= (\frac{b_{c_y}^{gt} - b_{c_y}}{c_h})^2 \quad \gamma = 2 - \Lambda
ρx​=(cw​bcx​gt​−bcx​​​)2,ρy​=(ch​bcy​gt​−bcy​​​)2γ=2−Λ
注意：这里的
(
c
w
,
c
h
)
(c_w, c_h)
(cw​,ch​)为真实框和预测框最小外接矩形的宽和高

（3）形状损失(Shape cost)，定义如下：

Ω
=
∑
t
=
w
,
h
(
1
−
e
−
w
t
)
θ
=
(
1
−
e
−
w
w
)
θ
+
(
1
−
e
−
w
h
)
θ
\Omega = \sum_{t=w, h}(1-e^{-w_t})^\theta=(1-e^{-w_w})^\theta+(1-e^{-w_h})^\theta
Ω=t=w,h∑​(1−e−wt​)θ=(1−e−ww​)θ+(1−e−wh​)θ
其中：

w
w
=
∣
w
−
w
g
t
∣
max
⁡
(
w
,
w
g
t
)
,
w
h
=
∣
h
−
h
g
t
∣
max
⁡
(
h
,
h
g
t
)
w_w=\frac{|w-w^{gt}|}{\max(w, w^{gt})}, \quad w_h=\frac{|h-h^{gt}|}{\max(h, h^{gt})}
ww​=max(w,wgt)∣w−wgt∣​,wh​=max(h,hgt)∣h−hgt∣​
$(w,h)$和
(
w
g
t
,
h
g
t
)
(w^{gt}, h^{gt})
(wgt,hgt)分别为预测框和真实框的宽和高，$\theta$控制对形状损失的关注程度，为了避免过于关注形状损失而降低对预测框的移动，作者使用遗传算法计算出$\theta$接近4，因此作者定于$\theta$参数范围为[2, 6]

（4）IoU损失(IoU cost)


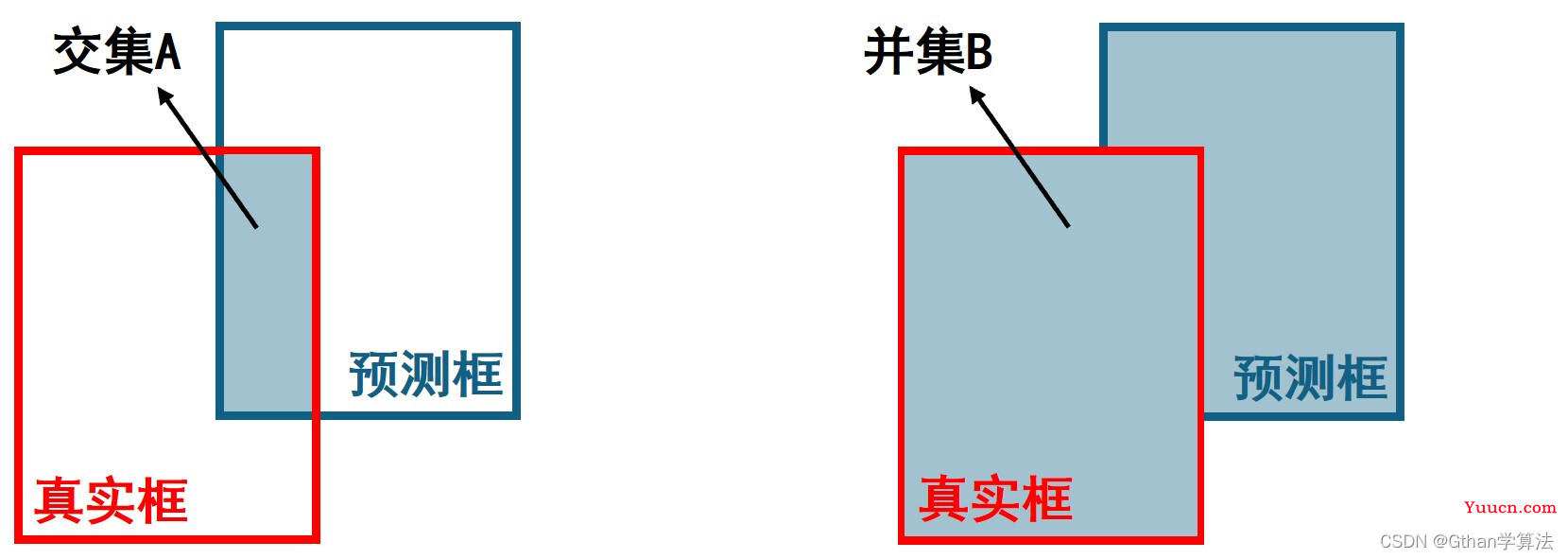
I
o
U
=
交
集
A
并
集
B
IoU=\frac{交集A}{并集B}
IoU=并集B交集A​

综上所诉，最终SIoU损失函数定义如下：

L
o
s
s
S
I
o
U
=
1
−
I
o
U
+
Δ
+
Ω
2
Loss_{SIoU}=1-IoU+\frac{\Delta + \Omega}{2}
LossSIoU​=1−IoU+2Δ+Ω​

1.2 代码实现

有关SIoU得代码实现如下(来源美团yolov6)：

elif self.iou_type == 'siou':
	# SIoU Loss https://arxiv.org/pdf/2205.12740.pdf
	'''
	预测框和真实框坐标形式为xyxy，即左下右上角坐标或左上右下角坐标
	'''
	s_cw = (b2_x1 + b2_x2 - b1_x1 - b1_x2) * 0.5 #真实框和预测框中心点的宽度差
	s_ch = (b2_y1 + b2_y2 - b1_y1 - b1_y2) * 0.5 #真实框和预测框中心点的高度差
	sigma = torch.pow(s_cw ** 2 + s_ch ** 2, 0.5) #真实框和预测框中心点的距离
	sin_alpha_1 = torch.abs(s_cw) / sigma #真实框和预测框中心点的夹角β
	sin_alpha_2 = torch.abs(s_ch) / sigma #真实框和预测框中心点的夹角α
	threshold = pow(2, 0.5) / 2 #夹角阈值
	sin_alpha = torch.where(sin_alpha_1 > threshold, sin_alpha_2, sin_alpha_1) #α大于45°则考虑优化β，否则优化α
	angle_cost = torch.cos(torch.arcsin(sin_alpha) * 2 - math.pi / 2) #角度损失
	rho_x = (s_cw / cw) ** 2 
	rho_y = (s_ch / ch) ** 2
	gamma = angle_cost - 2
	distance_cost = 2 - torch.exp(gamma * rho_x) - torch.exp(gamma * rho_y) #距离损失
	omiga_w = torch.abs(w1 - w2) / torch.max(w1, w2)
	omiga_h = torch.abs(h1 - h2) / torch.max(h1, h2)
	shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), 4) + torch.pow(1 - torch.exp(-1 * omiga_h), 4) #形状损失
	iou = iou - 0.5 * (distance_cost + shape_cost) #siou
loss = 1.0 - iou