对于下图所示的二叉树

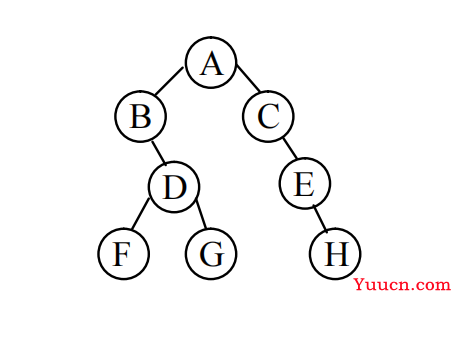
其先序、中序、后序遍历的序列如下：

• 先序遍历： A、B、D、F、G、C、E、H
• 中序遍历： B、F、D、G、A、C、E、H
• 后序遍历： F、G、D、B、H、E、C、A
• 层序遍历： A、B、C、D、E、F、G、H

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

前序遍历

先序遍历操作过程：

若二叉树为空，则空操作，否则依次执行如下3个操作

1. 访问根结点；
2. 按先序遍历左子树；
3. 按先序遍历右子树。

递归法

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<Integer>();
        preorder(root, list);
        return list;
    }
    public void preorder(TreeNode root, List<Integer> list){
        if (root == null) return;
        list.add(root.val);
        preorder(root.left, list);
        preorder(root.right, list);
    }
}

迭代法

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        if (root != null) stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.peek();
            list.add(stack.pop().val);
            if (node.right != null) stack.push(node.right);
            if (node.left != null) stack.push(node.left);
        }
        return list;
    }
}

中序遍历

中序遍历操作过程：

若二叉树为空，则空操作，否则依次执行如下3个操作

1. 按中序遍历左子树；
2. 访问根结点；
3. 按中序遍历右子树。

递归法

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<Integer>();
        inorder(root, list);
        return list;
    }
    public void inorder(TreeNode root, List<Integer> list){
        if (root == null) return;
        inorder(root.left, list);
        list.add(root.val);
        inorder(root.right, list);
    }
}

迭代法

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        ArrayList<Integer> list = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode node =  root;
        while (node != null || !stack.isEmpty()){
            if (node != null){
                stack.push(node);
                node = node.left;
            }else{
                node = stack.peek();
                list.add(stack.pop().val);
                node = node.right;
            }
        }
        return list;
    }
}

后序遍历

后序遍历操作过程：

若二叉树为空，则空操作，否则依次执行如下3个操作：

1. 按后序遍历左子树；
2. 按后序遍历右子树；
3. 访问根结点。

递归法

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<Integer>();
        postorder(root, list);
        return list;
    }
    public void postorder(TreeNode root, List<Integer> list){
        if (root == null) return;
        postorder(root.left, list);
        postorder(root.right, list);
        list.add(root.val);
    }
}

迭代法

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode prev = null; // 记录上一个输出的结点
        while (root != null || !stack.isEmpty()){
            while (root != null) { // 从当前结点向“左下”遍历，找到位于“左下”方的结点
                stack.push(root);
                root = root.left;
            }
						// 定位到没有左子树的结点，接着准备处理右边（要弹出是因为如果有右子树，是要先让右子树进栈的）
            root = stack.pop(); 
						/*因为通过刚才的遍历知道不存在左子树了，现在开始向右走，下面的操作都是在没有左子树的前提下进行的*/
						/*将当前结点值输出的条件是：【当前结点没有右子树】 或 【右子树的值已经输出过轮到当前结点了】*/
            if (root.right == null || root.right == prev) {
                list.add(root.val); // 将当前结点的值输出
                prev = root; // 用prev记录输出的结点
                root = null;
            }else{
                stack.push(root);
                root = root.right;
            }
        }
        return list;
    } 
}

如果有左子树，就一直走下去；如果有右子树，则往右子树走一步，再一直往左走下去。

层序遍历

层序遍历，又称广度优先遍历。

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> list = new ArrayList<>();
        ArrayDeque<TreeNode> queue = new ArrayDeque<>();
        if(root != null) queue.offer(root);
        while (!queue.isEmpty()){
            int size = queue.size();
            ArrayList<Integer> tmp = new ArrayList<>();
            for (int i = 0; i < size; i++){
                TreeNode node = queue.poll();
                tmp.add(node.val);
                if (node.left != null) queue.offer(node.left);
                if (node.right != null) queue.offer(node.right);
            }
            list.add(tmp);
// 若要返回其节点值自底向上的层序遍历，只需反转得到的list即可
// Collections.reverse(list);
        }
        return list;
    }
}