哈夫曼树
1.概念:
- 给定n个权值最为n个叶子的节点,构建成一颗二叉树。如果次树的带权路径长度最小,则称此二叉树为最优二叉树,也叫哈夫曼树。
-
WLP:带权路径长度
-
公式:

-
Wk:第k个叶子的节点权值
-
Lk:根节点到第k个叶子的节点长度
-
例如下列二叉树:
- 给定4个叶子节点,权值分别为{2,3,5,8},可以构造出4中形状不同的二叉树,但它们的带权路径长度可能不同。
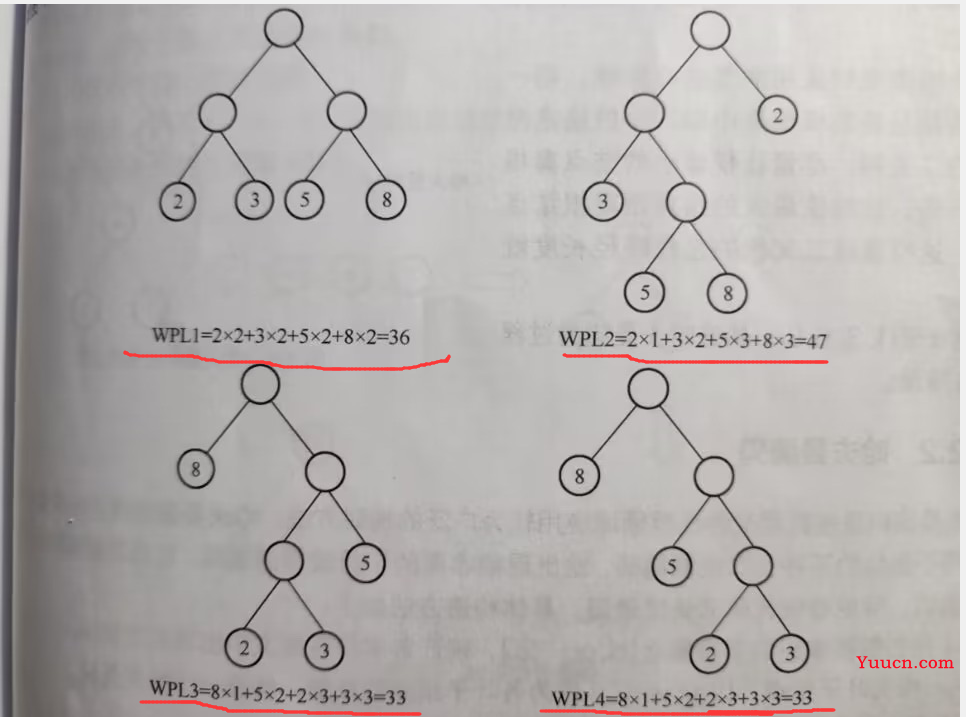
如上图可看出:1、最后两个树的带权路径长度相同且也是最小的,所以可看作哈夫曼树
2、权值最小的节点越靠下,越大越靠近根节点
2.构建哈夫曼树
(1)、在{2,3,5,8}这几个节点看作叶子节点(即后面没有子节点)
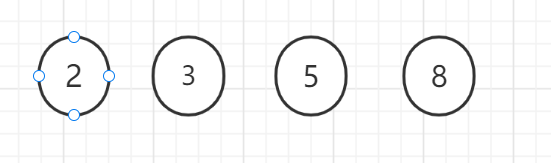
(2)、在这几个节点中选出权值最小和次小的两个节点。构成一个新二叉树(最小为左字节的、次小为右子节点),新二叉树的权值为这两个权值之和.
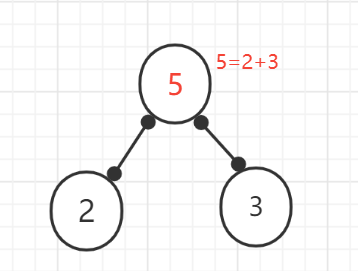
(3)、删除已经使用过的节点。将新创建的节点加入到还没被使用过的节点集合中,找出最小和次小的节点权值。又构成一颗新的二叉树。
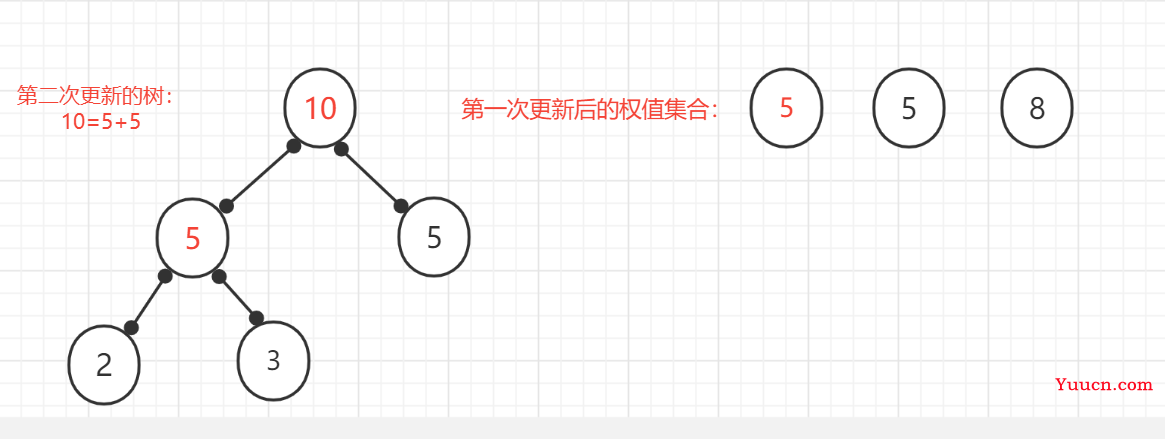
(4)、重复(2)的操作
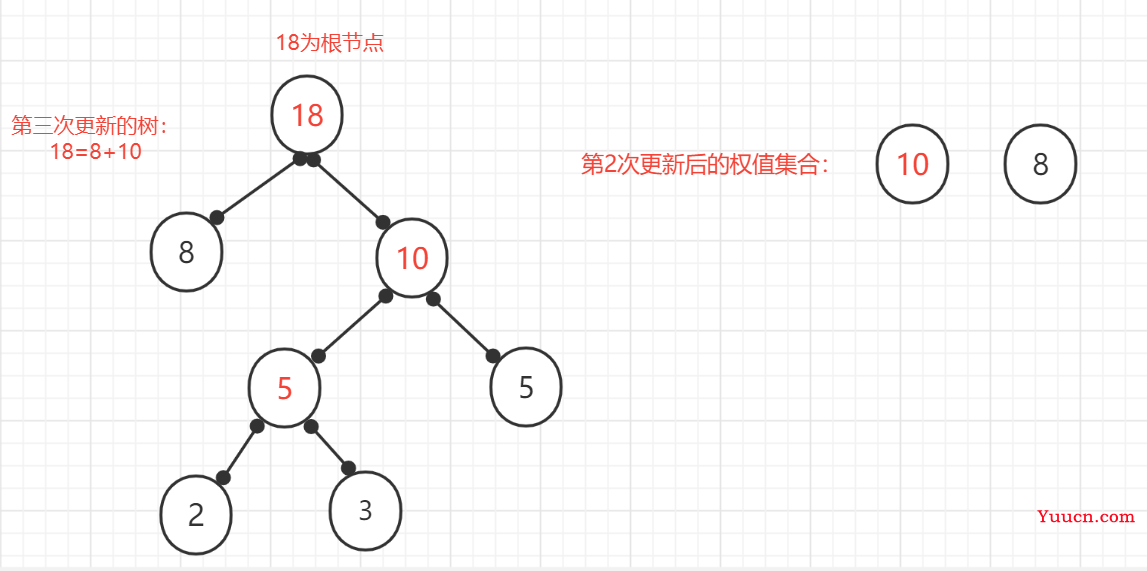
(5)、重复上面操作:删除已使用的节点,将新的节点加入未使用节点的集合中,发现只有一个节点,其权值为18.则此哈夫曼树创建完成,根节点权值为18.
代码如下:
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
/**
* 构造哈夫曼树
*/
public class test1 {
public static void main(String[] args) {
int[] arr={2,3,5,8};
//调用自定义的哈夫曼树方法,生成哈夫曼树
hafmantree(arr);
}
/**
* ,构造哈夫曼数方法
*
* @param arry
*/
public static void hafmantree(int[] arry) {
//创建集合用于存放节点值
List<Node> nlis = new ArrayList<Node>();
//遍历集合
for (int value : arry) {
//将每个数组元素看作Node节点对象,并存入list集合内
nlis.add(new Node(value));
}
/*
由于集合中存入的是一个个的Node对象,而Node对象已经被我们声明成了按照从小到大的可排序对象。
所以这里我们为可以通过Collections工具类中的sort方法进行排序
*/
//循环条件:只有一个节点,即最终根节点
while (nlis.size() > 1) {
Collections.sort(nlis);
//查看集合中还未被使用的节点
System.out.println(nlis);
//到了这里说明集合中的所有节点(权值)都是按照从小到大的顺序
//获取最小的节点值(二叉树左节点):子节点
Node lileft = nlis.get(0);
//获取第2小的节点值(二叉树右节点):子节点
Node lireght = nlis.get(1);
/*创建新的Node节点对象(二叉树):
此节点对象是最小的两个节点之和所生成的最新的节点。三个节点可以看成一个二叉树,即:
根节点(insternode对象)、左子节点(lileft.value)、右子节点(lireght.value)
*/
Node insternode = new Node(lileft.value + lireght.value);
//此二叉树的左节点
insternode.left = lileft;
//此二叉树的右节点
insternode.right = lireght;
//删除已经被处理过的节点
nlis.remove(lileft);
nlis.remove(lireght);
//将最新的节点加入到list集合中
nlis.add(insternode);
//重新对最新的list数组进行排序
Collections.sort(nlis);
}
//查看最终根节点
System.out.println(nlis);
}
}
/**
* ,构造哈夫曼数节点类,
* 此类也可以看成一个二叉树:根节点(Node对象)、左节子点(left)、右字节点(right)
* 实现Comparable接口:说明此类是可通过Collections工具类排序的,
*/
class Node implements Comparable<Node> {
int value; //每个节点的值(权值)
Node left; //每个二叉树的左指向节点
Node right; //每个二叉树的右指向节点
//构造方法,这里只需要初始化value实例变量,用于对象的赋值,而 left 与 right 本身就是此对象,可直接用于value赋值
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
//支持从小到大排序
@Override
public int compareTo(Node o) {
return this.value - o.value;
}
}
结果:
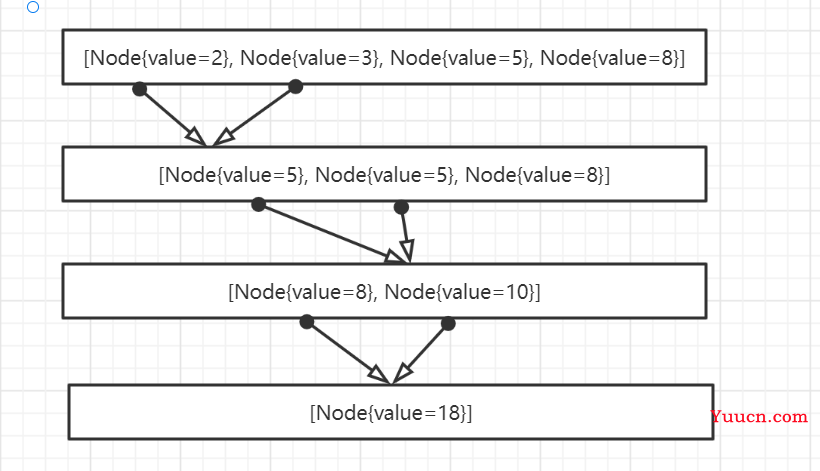
3.构建哈夫曼编码
-
这里是对一段字符串进行哈夫曼编码,所以需要先处理字符串
-
在哈夫曼树的基础上,规定了路径编码。
-
遍历已经创建好了的哈夫曼树,从它的根节点遍历次树到叶子节点,左子路径编码:0 、右子路径编码:1
import java.util.*;
/**
* 构造哈夫曼数+生成哈夫曼编码,编程实现。
*/
public class test1 {
public static void main(String[] args) {
//需要转换为哈夫曼编码的字符串
String valus="asdsgddbhj ,sjsh";
//将字符串存以node对象存入list集合中
List<Node> list = ListAndNode(valus);
//生成哈夫曼树
Node node = HFMTree(list);
//得到哈夫曼编码
HFMTable(node,"",andindex);
System.out.println(yezijied); //{32=1010, 97=1011, 98=1100, 115=01, 100=111, 103=1101, 104=001, 106=100, 44=000}
}
/*
第四步:
创建哈夫曼编码表:将叶子节点以0、1表示。0===》向左子节点走。1===》向右子节点走
yezijied:存放叶子节点对应的哈夫曼编码。此集合作业与全局
andindex:拼接编码。(拼接对应的0或1,形参最终的哈夫曼编码)
*/
static Map<Byte,String> yezijied=new HashMap<>();
static StringBuilder andindex=new StringBuilder();
/**
*
* @param node:节点
* @param index:路径表示:左路径为0.右路劲为1
* @param sub:拼接路径,使其成为对应叶子节点的哈夫曼码
*/
public static void HFMTable(Node node,String index,StringBuilder sub){
//
StringBuilder gitindex=new StringBuilder(sub);
//拼接路径
gitindex.append(index);
//如果节点为空就不需要处理
if (node!=null) {
//如果当前节点不是叶子节点
if (node.value == null) {
//如果节点不为空就递归其左边节点。并设置向左为0
HFMTable(node.left, "0", gitindex);
//如果节点不为空就递归其右边节点。并设置向右为1
HFMTable(node.right, "1", gitindex);
} else {
//为叶子节点就将其存入map集合中
yezijied.put(node.value, gitindex.toString());
}
}
}
/*
第三步:
@param nodes:已经存入list集合中的Node节点
创建字符串的哈夫曼树结构
*/
public static Node HFMTree(List<Node> nodes){
//循环条件:节点数必须大于1.如果等于1就是一个节点(根节点),没有分支
while (nodes.size()>1){
//排序list集合,根据权值(节点个数)从小到大排序
Collections.sort(nodes);
/*
创建一个二叉树:
feiyezijied:根节点
nodeleft:左子节点
noderight:右子节点
*/
//得到权值最小的两个节点.这两个节点分别可看作左右两个子节点
Node nodeleft = nodes.get(0);
Node noderight = nodes.get(1);
//创建新的Node对象:这可以想象为两个叶子节点生成的根节点,
// 由于哈夫曼数的原理,需要编码的值是叶子节点,而叶子节点上的父节点只是通过叶子节点虚拟创建的节点,
// 是为了形成一整颗完整的树。所以它是没有字符串原始值,,其可用两个字节的权值之和标记
Node feiyezijied=new Node(null,nodeleft.quanzhi+noderight.quanzhi);
//Node对象的左字节点
feiyezijied.left=nodeleft;
//Node对象的右字节点
feiyezijied.right=noderight;
//删除原集合中的以使用的节点对象.即上面已经每次获得的集合中两个最小的节点
nodes.remove(nodeleft);
nodes.remove(noderight);
//将新创建的Node节点加入list集合中
nodes.add(feiyezijied);
//重新对list集合排序
Collections.sort(nodes);
}
//返回最终根节点
return nodes.get(0);
}
/*
第二步:
@param valus:传入需要编码的字符串,将其变成节点
将需要编码的字符串,每个原始值(ASCIIM码)以节点(Node)对象形式传入list集合中。
而节点对象Node初始化了value与quanzhi,所以节点对象是包括这两个值,所以将每个节点对象当作一个map.
设k=value、v=quanzhi
*/
public static List<Node> ListAndNode(String valus){
//将字符对象存入byte数组。
byte[] bytes = valus.getBytes();
//创建List集合
List<Node> nodes=new ArrayList<>();
//创建Map集合
Map<Byte,Integer> node=new HashMap<>();
//遍历bytes数组,得到每个字符串的原始值
for (byte by:bytes){
//先试着通过传入的第一个k获取v
Integer index = node.get(by);
//如果map集合中此原始值对应的个数还没有
if (index==null){
node.put(by,1);
}else {
node.put(by,index+1);
}
}
//遍历map集合,并将每次遍历的元素,以Node对象的形式存入list集合
for (Map.Entry<Byte,Integer> n:node.entrySet()){
nodes.add(new Node(n.getKey(),n.getValue()));
}
//最后返回此list集合
return nodes;
}
}
/*
第一步:
节点类:其本身可可看作一个概念性的二叉树
Node对象本身可看作是一个二叉树的根节点
实现Comparable接口:泛型规定此接口作用与此Node节点,说明此类是可排序的,通过' Collections.sort()'
*/
class Node implements Comparable<Node>{
Byte value; //原始值:字符本身的ASCIIM码。因为一段字符串中有许多相同的字符,但相同字符却对应这一个ASCIIM码
int quanzhi; //此字符value在一段字符串中出现的次数
Node left; //Node对象看作是二叉树的根节点,那么这就是此二叉树的左子节点
Node right; //Node对象看作是二叉树的根节点,那么这就是此二叉树的右边子节点
//构造器初始化 value 、quanzhi。
public Node(Byte value, int quanzhi) {
this.value = value;
this.quanzhi = quanzhi;
}
//重写toString:因为我们需要拿到这两个值
@Override
public String toString() {
return "Node{" +
"value=" + value +
", quanzhi=" + quanzhi +
'}';
}
//实现Comparable接口中的方法:手动设置排序规则
@Override
public int compareTo(Node o) {
//设置为通过权值从小到大排序
return this.quanzhi-o.quanzhi;
}
//前序遍历
public void qxbl(){
//先输出当前节点,也就是根节点
System.out.println(this);
//如果左子节点不是null节点,就递归遍历输出左子节点.null表示不是叶子节点
if (this.left!=null){
this.left.qxbl();
}
//同样递归右子节点
if (this.right!=null){
this.right.qxbl();
}
}
}