1. 线性表

1. 线性表的定义
   1. 特点：
      1. 存在唯一一个被称为第一个的数据元素
      2. 存在唯一一个被称为最后一个的数据元素
      3. 除了第一个元素之外，其他的数据元素都有唯一一个直接前驱
      4. 除了最后一个元素之外，其他的数据元素都有唯一一个直接后驱
   2. 定义：是由 \(n(n\ge 0)\) 个相同的数据元素组成的有限序列
   3. 逻辑特征
      1. 有限性：数据元素的个数是有限的
      2. 相同性：数据元素的元素类型是相同的
      3. 相继性（线性性）：\(a_1\) 为表中的第一个元素，无前驱元素，\(a_n\) 为表中最后一个元素，无后驱元素；对于 \(1<i<n\) ， \(a_{i-1}\) 为 \(a_{i}\) 的直接前驱， \(a_{i+1}\) 为 \(a_{i}\) 的直接后驱
   4. 基本操作 \(Operations\)
      1. 求线性表的长度 Lenlist(L)
      2. 获取线性表中的元素 GetElem(L , i)
      3. 通过值来查找线性表当中的元素 SearchElem(L , Val)
      4. 插入元素 InsertElem(L , i , Elem)
      5. 删除元素 DeleteElem(L , i)
2. 线性表的存储结构设计

   1. 连续存储结构(数组)

      1. 存储方式：依次将元素存放进连续的存储空间中
      2. 顺序表示： \(loc(a_i) = loc(a_1)+(i-1)*c\)
      3. 存储特点：逻辑上相邻的元素，物理结构上也相邻
      4. \(Operations\)

      // 1. 插入元素 O(n)
      int insertElem(list *L , Datatype x , int i){
          if((*L).last >= maxsize - 1){   //overflow
              printf("Overflow\n");
              return -1;
          }
          else if(i < 1 || i > (*L).last + 1){    //wrong location
              printf("Error\n");
              return -1;
          }
          else{
              for(int j = (*L).last ; j >= i ; --j){  //move the elements
                  (*L).data[j + 1] = (*L).data[j];
              }
              (*L).data[i] = x;
              (*L).last++;
          }
          return 1;
      }
      

      // 2. 删除元素 O(n)
      int deleteElem(list *L , int i){
          if(i < 1 || i > (*L).last + 1){    //wrong location
              printf("Error\n");
              return -1;
          }
          else {
              for(int j = i ; j <= (*L).last ; ++j){
                  (*L).data[j - 1] = (*L).data[j];
              }
              (*L).last--;
          }
      }
      

      // 3. 按值查找 O(n)
      int searchElem(list *L , Datatype x){
          int i = 1;
          while(i <= (*L).last && x != (*L).data[i - 1]){
              ++i;
          }
          if(i <= (*L).last) return i - 1;
          return -1;  //can not find
      }
      

      // 4. 按位置查找 O(1)
      int getElem(list *L , int i){
          if(i < 1 || i > (*L).last + 1){    //wrong location
              printf("Error\n");
              return -1;
          }
          return (*L).data[i - 1]
      }
      

      5. 连续存储的优缺点
         1. 优点
            1. 顺序表的存储结构简单
            2. 随机存储，按位置取值速度快
            3. 存储效率高，无需增加逻辑关系的占用空间
         2. 缺点
            1. 删除插入速度慢
            2. 预先分配内存大

\(\quad\)
\(存储效率 = \frac{数据元素占用空间}{数据元素占用空间+逻辑关系占用空间}\)
\(\quad\)

2. 链式存储结构

   1. 存储方式：用一组任意的存储单元存储线性表中的数据元素，通过每个结点的指针将数据元素连接在一起
   2. 单链表：具有一个指针，指向后继元素

   typedef struct Node{
       datatype data;
       struct Node *next;
   }Node , *head;
   

   3. \(Operations\)

   // 1. 建立单链表
   void createList(){
       Node head = new Node();
       head->next = NULL;
   }
   

   // 2. 插入元素
   int insertList(Node &L , int i , datatype x){
       Node *p = head;
       int j = 0;
       while(p && j < i - 1){
           p = p->next;
           j++;
       }
       if(!p) return -1;
       Node *temp = new Node;
       temp->data = x;     // insert
       temp->next = p->next;
       p->next = temp;
       return 1;
   }
   

   // 3. 删除元素
   int deleteList(Node &L , int i){
       Node *p = head;
       int j = 0;
       while((p->next) && j < i - 1){
           p = p->next;
           j++;
       }
       if(!(p->next)) return -1;
       Node *temp = p->next;
       p->next = temp->next;
       delete temp;
       return 1;
   }
   

   // 4. 通过位置查找元素
   datatype getList(Node &L , int i){
       Node *p = head;
       int j = 0;
       while(p && j < i - 1){
           p = p->next;
           j++;
       }
       if(!p) return -1;
       return p->data;
   }
   

   // 5. 通过值来查找元素
   int searchList(Node &L , datatype x){
       Node *p = head;
       int j = 0;
       while(p && p->data != x){
           p = p->next;
           ++j;
       }
       if(!p) {
           printf("Not Find!");
           return -1;
       }
       return j;
   }
   

   4. 双链表：前驱指针 *prev 和后继指针 *next
   5. \(Operations\) 要处理两个指针

   // 1. 初始化
   typedef struct DulNode{
       datatype data;
       struct DulNode *prev , *next;
   }DulNode , *head;
   

   // 2. 插入元素(先右后左)
   s->data = _data;
   s->next = p->next;
   p->next->prev = s;
   p->next = s;
   s->prev = p;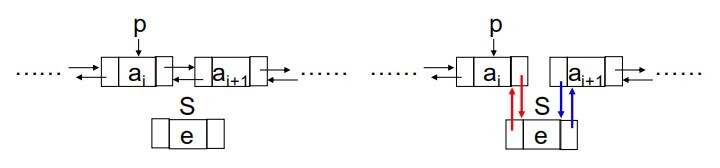
   

   

   // 3. 删除元素
   p->prev->next = p->next;
   p->next->prev = p->prev;
   delete p;
   

• 连续设计和连接设计的对比
  

  Parameters	连续设计	链接设计
  表的容量	固定，不易扩充	灵活，易扩充
  存取操作	随机访问存取，速度快	顺序访问存取，速度慢
  时间	插入、删除操作费时间	访问元素费时间
  空间	估算长度，浪费空间	实际长度

3. 链接存储设计的数组实现
   

   data	next
   data1	1
   2
   \(\cdots\)	\(\cdots\)
   max_size - 1
   -1

   1. 结点：

   #define max_size 1024    \\数组最大容量
   typedef int datatype;
   typedef int cursor;
   typedef struct{
    datatype data;
    cursor next;
   }node;
   node nodepool[max_size];     // 存储池（数组）
   cursor avail;    // 空闲空间的位置
   

   2. 初始化

   for(int i=0; i < max_size - 1; i++){
        nodepool[i].next = i + 1;
   }
   nodepool[max_size - 1].next = -1;
   avail = 0;   //avail 初始化
   

   3. 结点 node 的分配

   cursor getNode(){
        cursor p;
        if(avail == -1) p = -1;
        else {
            p = avail;
            avail = nodepool[avail].next;
        }
        return p;
    }
   

   4. 结点 node 的回收

   void freeNode(cursor p){
        nodepool[p].next = avail;
        avail = p;
   }
   

   5. 静态链表查找算法

   cursor findNode(cursor L , int i){
        cursor p = L;
        int j = 0;
        while(nodepool[p].next != -1 && (j < i>)){
            p = nodepool[p].next;
            ++j;
        }
        if(i == j) return p;
        else return -1;
   }
   

2. \(Applications\)

1. 合并有向链表

   ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
   	ListNode* preHead = new ListNode(-1);
   	ListNode* prev = preHead;
   	while (l1 != nullptr && l2 != nullptr) {
   		if (l1->val < l2->val) {
   			prev->next = l1;
   			l1 = l1->next;
   		} 
   		else {
   			prev->next = l2;
   			l2 = l2->next;
   		}
   		prev = prev->next;
   	}
   	prev->next = (l1 == nullptr) ? l2 : l1;// 合并剩余链表
   	return preHead->next;
   }
   

2. 反转链表

   1. 就地反转
   graph LR
   A(head)-.->B(nextp)
   B-->C(cur)
   C--> D(p)
   D-.->E(NULL)

   反转箭头为：

   graph LR
   A(head)-.->B(nextp)
   B-.->C(cur)
   C==>B
   C--> D(p)
   D-.->E(NULL)

    ListNode* reverseList(ListNode* head) {
    	if(head == nullptr) return head;
    	ListNode* nextp = nullptr;
    	ListNode* cur = head;
    	ListNode* p = head -> next;
    	while(p){
    		cur -> next = nextp;
    		nextp = cur;
    		cur = p;
    		p = cur -> next;
    	}
    	cur -> next = nextp;
    	return cur;
    }
   

   2. 递归：处理好 k之后，将 k-1 的箭头倒转；
   graph LR
   A(1)-->B(2)
   B-.-C(k -1)
   C-.-> D(k)
   D==>C
   E(k+1)-->D
   F(n)-.->E

   ListNode* reverseList(ListNode* head) {
       if(!head || !(head -> next)) return head;
       ListNode* new_Head =  reverseList(head -> next);
       head -> next -> next = head;
       head -> next = nullptr;
       return new_Head;
   }