
三剑客之Scipy
前面已经说过,最初的numpy其实是scipy的一部分,后来才从scipy中分离出来。scipy函数库在numpy库的基础上增加了众多的数学、科学以及工程计算中常用的库函数。例如线性代数、常微分方程数值求解、信号处理、图像处理、稀疏矩阵等等。由于其涉及的领域众多,我之于scipy,就像盲人摸大象,只能是摸到哪儿算哪儿。
一、插值
数据插值是数据处理过程中经常用到的技术,常用的插值有一维插值、二维插值、高阶插值等,常见的算法有线性插值、B样条插值、临近插值等。
1、一维插值
一维插值最常用的算法是线型插值和三阶样条插值,此外还有前点插值、后点插值、临近点插值、零阶插值(等同于前点插值)、一阶插值(等同于线性插值)、五阶插值等。下面的例子对以上8中插值方法进行了比较。
importnumpyasnp
fromscipyimportinterpolate
importmatplotlib.pyplotasplt
plt.rcParams['font.sans-serif']=['FangSong']
plt.rcParams['axes.unicode_minus']=False
x=np.linspace(0,10,11)
y=np.exp(-x/3.0)
x_new=np.linspace(0,10,100)#期望在0-10之间变成100个数据点
f1=interpolate.interp1d(x,y,kind='linear')
f2=interpolate.interp1d(x,y,kind='nearest')
f3=interpolate.interp1d(x,y,kind='zero')
f4=interpolate.interp1d(x,y,kind='slinear')
f5=interpolate.interp1d(x,y,kind='cubic')
f6=interpolate.interp1d(x,y,kind='quadratic')
f7=interpolate.interp1d(x,y,kind='previous')
f8=interpolate.interp1d(x,y,kind='next')
plt.figure('Demo',facecolor='#eaeaea')
plt.subplot(221)
plt.plot(x,y,"o",label=u"原始数据")
plt.plot(x_new,f2(x_new),label=u"临近点插值")
plt.plot(x_new,f7(x_new),label=u"前点插值")
plt.plot(x_new,f8(x_new),label=u"后点线性插值")
plt.legend()
plt.subplot(222)
plt.plot(x,y,"o",label=u"原始数据")
plt.plot(x_new,f1(x_new),label=u"线性插值")
plt.plot(x_new,f3(x_new),label=u"零阶样条插值")
plt.plot(x_new,f4(x_new),label=u"一阶样条插值")
plt.legend()
plt.subplot(223)
plt.plot(x,y,"o",label=u"原始数据")
plt.plot(x_new,f1(x_new),label=u"线性插值")
plt.plot(x_new,f5(x_new),label=u"三阶样条插值")
plt.legend()
plt.subplot(224)
plt.plot(x,y,"o",label=u"原始数据")
plt.plot(x_new,f1(x_new),label=u"线性插值")
plt.plot(x_new,f6(x_new),label=u"五阶样条插值")
plt.legend()
plt.show()
不同的插值方法画在一起,对比之下效果会比较明显:
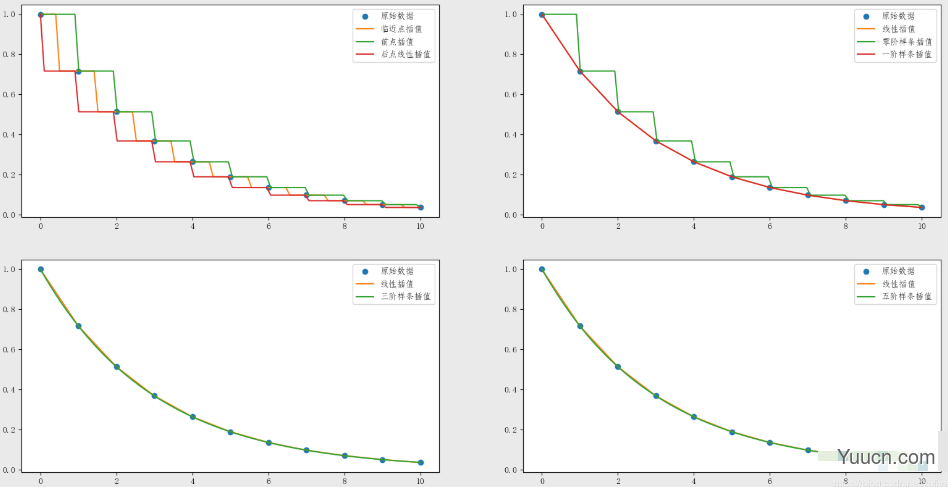
2、二维插值
二维数据,通常总是对应着一个网格,比如,经纬度网格。如果插值对象只有一个二维数组,那么我们可以用数组的行列号来构造网格。
importnumpyasnp
fromscipyimportinterpolate
importmatplotlib.pyplotasplt
plt.rcParams['font.sans-serif']=['FangSong']
plt.rcParams['axes.unicode_minus']=False
y,x=np.mgrid[-2:2:20j,-3:3:30j]#30x20=600
z=x*np.exp(-x**2-y**2)
y_new,x_new=np.mgrid[-2:2:80j,-3:3:120j]#120x80=9600
f1=interpolate.interp2d(x[0,:],y[:,0],z,kind='linear')#线性插值
f2=interpolate.interp2d(x[0,:],y[:,0],z,kind='cubic')#三阶样条
f3=interpolate.interp2d(x[0,:],y[:,0],z,kind='quintic')#五阶样条
z1=f1(x_new[0,:],y_new[:,0])
z2=f2(x_new[0,:],y_new[:,0])
z3=f3(x_new[0,:],y_new[:,0])
plt.subplot(221)
plt.pcolor(x,y,z,cmap=plt.cm.hsv)
plt.colorbar()
plt.axis('equal')
plt.subplot(222)
plt.pcolor(x_new,y_new,z1,cmap=plt.cm.hsv)
plt.colorbar()
plt.axis('equal')
plt.subplot(223)
plt.pcolor(x_new,y_new,z2,cmap=plt.cm.hsv)
plt.colorbar()
plt.axis('equal')
plt.subplot(224)
plt.pcolor(x_new,y_new,z3,cmap=plt.cm.hsv)
plt.colorbar()
plt.axis('equal')
plt.show()
原始数据、线型插值数据、三阶插值数据、五阶插值数据的效果对比如下:
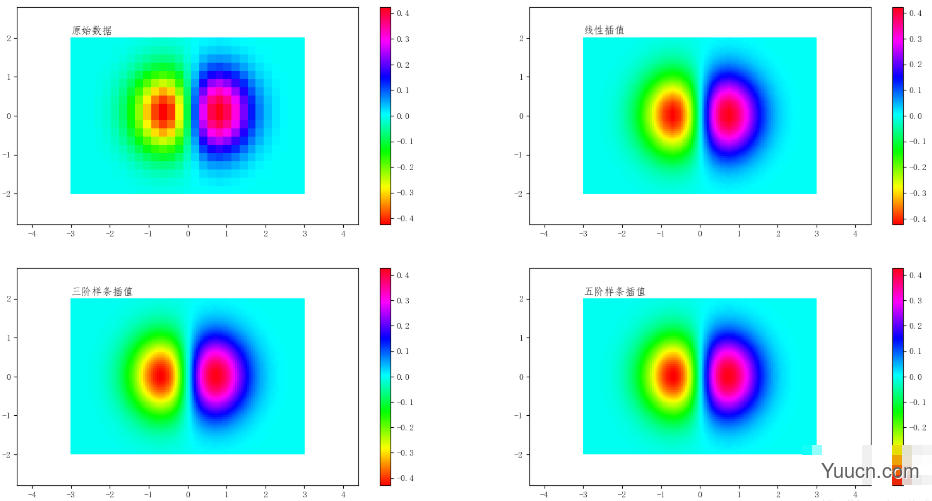
二、拟合
在工作中,我们常常需要在图中描绘某些实际数据观察的同时,使用一个曲线来拟合这些实际数据。所谓拟合,就是找出符合数据变化趋势的曲线方程,进而对变化趋势做出预测。
1、使用numpy.polyfit拟合
numpy.polyfit() 实现了最小二乘法,其功能是返回指定次数的多项式参数,这组参数使得多项式和样本数据的误差为最小。下面的代码,虚拟了谷神星的一段观测数据,籍此使用最小二乘法实现多项式拟合,进而推测出谷神星未来的运行轨迹。最后和虚拟的运行轨道方程比较。
#coding:utf-8
importnumpyasnp
importmatplotlib.pyplotasplt
plt.rcParams['font.sans-serif']=['FangSong']
plt.rcParams['axes.unicode_minus']=False
deff(t):
"""谷神星虚拟的运行轨道方程。我们假装不知道,仅用来验证预测结果是否准确"""
t=t/7.5-1
return((t**2-1)**3+0.5)*np.sin(2*t)
t=np.linspace(0,20,201)#用于绘制实际的运行轨迹线
_x=np.linspace(0,15,16)#观测数据时间序列
_y=f(_x)#观测数据位置序列
x=np.linspace(15,20,6)#待预测的时间序列
loss_list=list()
foriinrange(2,16):#从2次到15次多项式,逐一计算误差
args=np.polyfit(_x,_y,i)#用最小二乘法找到一组系数
g=np.poly1d(args)#用这组系数生成方程g(x)
loss=np.sum(np.square(g(_x)-_y))#计算i次多项式拟合的误差
loss_list.append(loss)
print(i,loss)
k=loss_list.index(min(loss_list))+2
args=np.polyfit(_x,_y,k)
g=np.poly1d(args)
plt.figure('demo',facecolor='#eaeaea')
plt.plot(_x,_y,c='r',ls='',marker='o',label=u'观测数据')
plt.plot(_x,g(_x),c='b',ls='-',label=u'%d次多项式拟合,误差%0.8f'%(k,loss_list[k-2]))
plt.plot(x,g(x),c='r',ls=':',label=u'预测轨迹')
plt.plot(t,f(t),c='#60f0f0',ls='--',label=u'实际运行轨迹')
plt.legend(loc='lowerleft')
plt.show()
将虚拟的运行轨道、虚拟的观测数据、拟合曲线、预测曲线绘制在一起,效果如下:
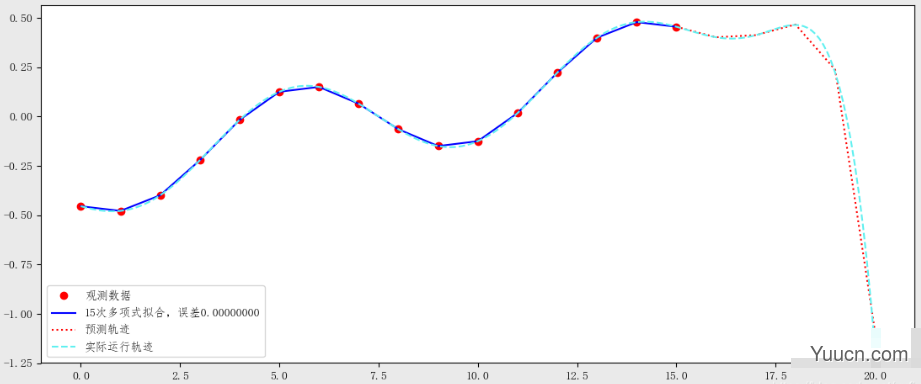
2、使用scipy.optimize.optimize.curve_fit拟合
不管曲线实际是什么样的,多项式拟合总是以一个有限次的多项式去逼近数据样本。还有一种拟合,就是我们知道曲线的标准方程,但有些系数或参数不确定,这样的拟合,也是要找到最佳系数或参数。scipy提供的拟合,需要先确定带参数的曲线方程,然后由scipy求解方程,返回曲线参数。
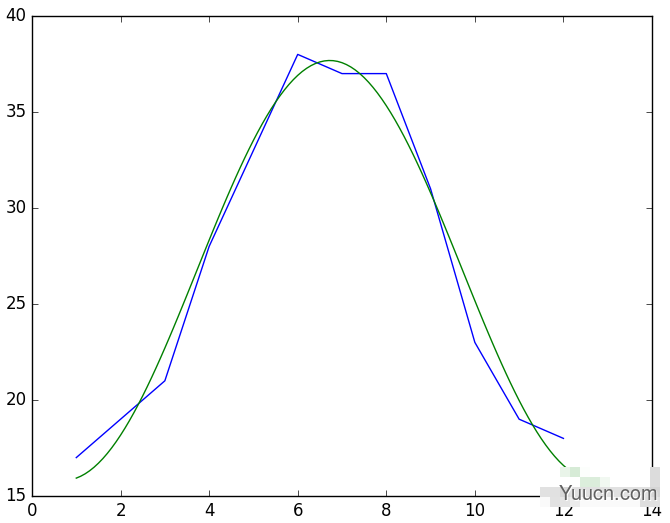
>>>importnumpyasnp >>>importmatplotlib.pyplotasplt >>>fromscipyimportoptimize >>>x=np.arange(1,13,1) >>>y=np.array([17,19,21,28,33,38,37,37,31,23,19,18]) >>>plt.plot(x,y) [<matplotlib.lines.Line2Dobjectat0x04799D10>] >>>plt.show()
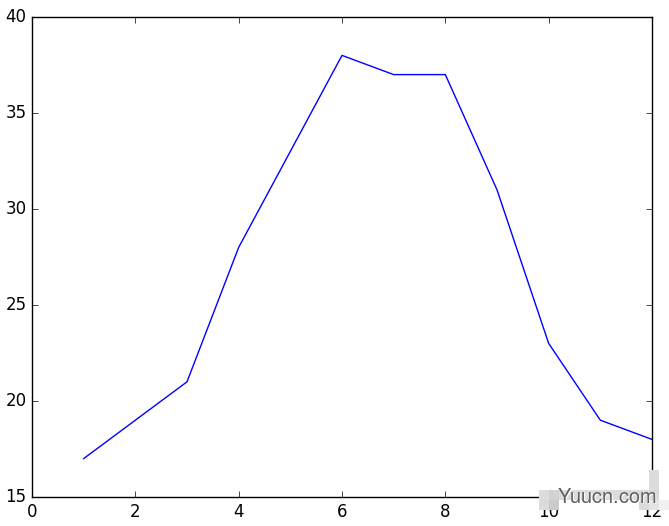
可以看出,曲线近似正弦函数。构建函数y=asin(xpi/6+b)+c,使用scipy的optimize.curve_fit函数求出a、b、c的值:
>>>deffmax(x,a,b,c): returna*np.sin(x*np.pi/6+b)+c >>>fita,fitb=optimize.curve_fit(fmax,x,y,[1,1,1]) >>>printfita [10.93254951-1.949609626.75] >>>xn=np.arange(1,13,0.1) >>>plt.plot(x,y) [<matplotlib.lines.Line2Dobjectat0x04B160B0>] >>>plt.plot(xn,fmax(xn,fita[0],fita[1],fita[2])) [<matplotlib.lines.Line2Dobjectat0x04B16510>] >>>plt.show()
三、求解非线性方程(组)
在数学建模中,需要对一些稀奇古怪的方程(组)求解,Matlab自然是首选,但Matlab不是免费的,scipy则为我们提供了免费的午餐!scipy.optimize库中的fsolve函数可以用来对非线性方程(组)进行求解。它的基本调用形式如下:
fsolve(func,x0)
func(x)是计算方程组误差的函数,它的参数x是一个矢量,表示方程组的各个未知数的一组可能解,func返回将x代入方程组之后得到的误差;x0为未知数矢量的初始值。
我们先来求解一个简单的方程:$ \sin(x) - \cos(x) = 0.2$
>>>fromscipy.optimizeimportfsolve >>>importnumpyasnp >>>deff(A): x=float(A[0]) return[np.sin(x)-np.cos(x)-0.2] >>>result=fsolve(f,[1]) array([0.92729522]) >>>printresult [0.92729522] >>>printf(result) [2.7977428707082197e-09]
哈哈,易如反掌!再来一个方程组:
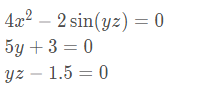
>>>fromscipy.optimizeimportfsolve >>>importnumpyasnp >>>deff(A): x=float(A[0]) y=float(A[1]) z=float(A[2]) return[4*x*x-2*np.sin(y*z),5*y+3,y*z-1.5] >>>result=fsolve(f,[1,1,1]) >>>printresult [-0.70622057-0.6-2.5] >>>printf(result) [-9.1260332624187868e-14,0.0,5.329070518200751e-15]
四、数值积分
数值积分是对定积分的数值求解,例如可以利用数值积分计算某个形状的面积。我们知道,半径为1的圆的方程可写成:
![]()
下面让我们来考虑一下如何计算半径为1的半圆的面积,根据圆的面积公式,其面积应该等于PI/2。单位半圆曲线可以用下面的函数表示:
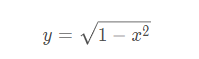
我们先定义一个计算根据x计算y的函数:
>>>defhalf_circle(x): return(1-x**2)**0.5
1、经典微分法
下面的程序使用经典的分小矩形计算面积总和的方式,计算出单位半圆的面积:
>>>N=10000 >>>x=np.linspace(-1,1,N) >>>dx=2.0/N >>>y=half_circle(x) >>>dx*np.sum(y[:-1]+y[1:])#面积的两倍 3.1412751679988937
2、使用定积分求解函数
如果我们调用scipy.integrate库中的quad函数的话,将会得到非常精确的结果:
>>>fromscipyimportintegrate >>>pi_half,err=integrate.quad(half_circle,-1,1) >>>pi_half*2 3.1415926535897984
五、图像处理
在scipy.misc模块中,有一个函数可以载入Lena图像——这副图像是被用作图像处理的经典示范图像。我只是简单展示一下在该图像上的几个操作。
(1)载入Lena图像,并显示灰度图像
(2)应用中值滤波扫描信号的每一个数据点,并替换为相邻数据点的中值
(3)旋转图像
(4)应用Prewitt滤波器(基于图像强度的梯度计算)
>>>fromscipyimportmisc
>>>fromscipyimportndimage
>>>img=misc.lena().astype(np.float32)
>>>plt.subplot(221)
>>>plt.title('OriginalImage')
>>>plt.imshow(img,cmap=plt.cm.gray)
>>>plt.subplot(222)
>>>plt.title('MedianFilter')
>>>filtered=ndimage.median_filter(img,size=(42,42))
>>>plt.imshow(filtered,cmap=plt.cm.gray)
>>>plt.subplot(223)
>>>plt.title('Rotated')
>>>rotated=ndimage.rotate(img,90)
>>>plt.imshow(rotated,cmap=plt.cm.gray)
>>>plt.subplot(224)
>>>plt.title('PrewittFilter')
>>>filtered=ndimage.prewitt(img)
>>>plt.imshow(filtered,cmap=plt.cm.gray)
>>>plt.show()
python学习网,大量的免费python视频教程,欢迎在线学习!
相关推荐:
1、Python数学建模三剑客之Numpy