CNN-LSTM数据驱动模型
6.1 基本原理
深度学习是机器学习前沿且热门的理论,而其中的两大框架卷积神经网络(CNN)以及长短期记忆网络(LSTM)是深度学习的代表,CNN能过够通过使用卷积核从样本数据中提取出其潜在的特征,而长短期记忆网络LSTM能够捕捉到长期的成分。近年来两者的结合成为研究的热点。卷积神经网络由卷积层和池化层交替叠加而成,在每个卷积层与池化层之间都有relu激活函数作用来加速模型的收敛,在模型中数据经过卷积神经网络的处理,所有特征融合后得到卷积神经网络的特征描述,此时传递数据给LSTM,通常情况下此时输入的数据需要reshape成LSTM处理的类型,LSTM得到新的输入后,确定需要保持与丢弃的,其中保持与丢弃借助sigmoid激活函数完成,任何数据乘1都为其本身,而任何函数乘0都为0,借助该即可选择遗忘以及保存重要的数据。当数据乘1时则代表被保留,从输入门中获取的数据即为我们更新了状态。最后借助输出门确定携带的信息,将新的状态,以及隐藏状态转移到下个时间步。
6.2 CNN-LSTM算法的实现
首先对于输入数据进行读取,本次的处理方法是CNN—LSTM故将数据类型reshape成CNN处理的数据类型,接下来进行数据的标准化处理,这里值得注意的是,搭建模型的目的是为了能够更好的得到预测的数据值,在多次的尝试了正规化的标准方法后,经过多次的调整参数发现,数据的损失始终无法降低到0.5以下下,此时为了输出数据更加的准确,调整了一下数据的标准化,数据依旧时正态分布,但期望值此时非0。
CNN的模块部分采用了两层卷积,两层最大池化,中间包含激活函数,此时CNN得到的数据无法直接输入到LSTM中 ,于是进行reshape使其符合LSTM的输入数据类型,通过LSTM层以及Dropout层的处理,最后在全连接层输出数据。

图6-1 CNN-LSTM模型
6.3 结果展示
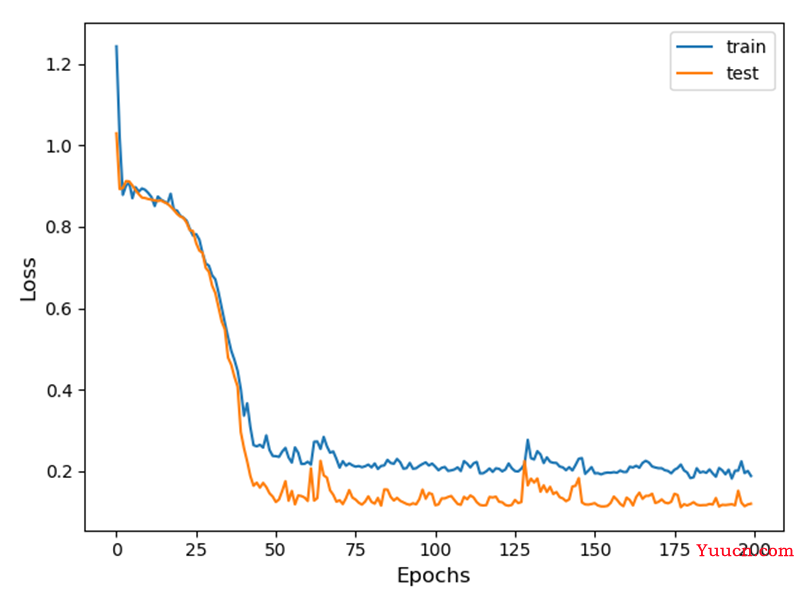
图6-2 训练过程中Loss变化曲线
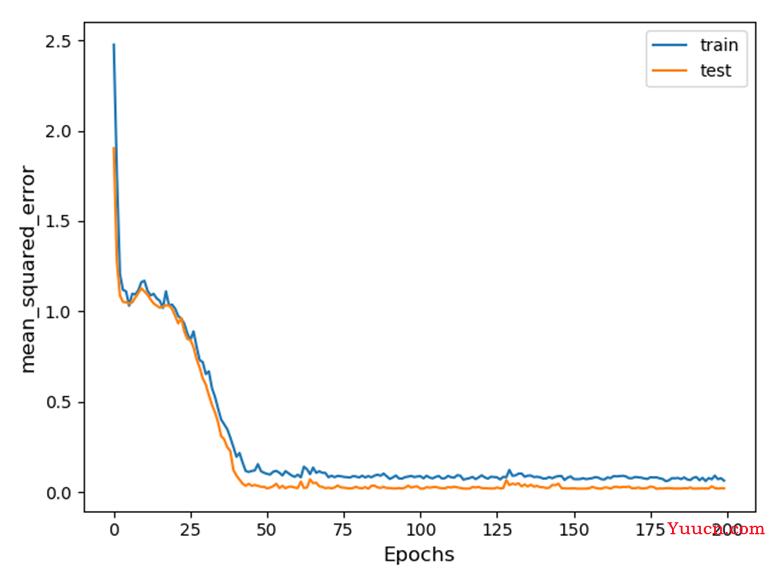
图6-3 训练过程中mse变化曲线
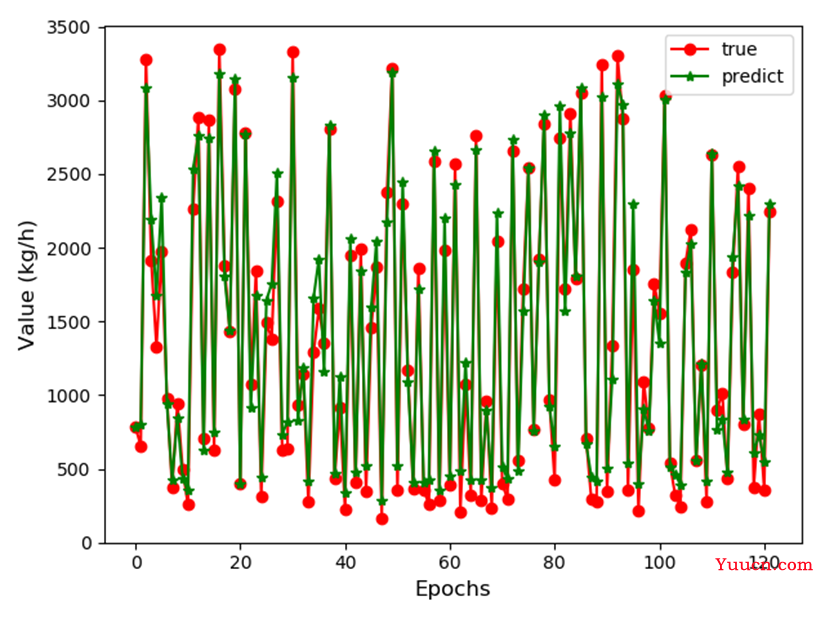
图6-4 真实值与预测值变化曲线
6.4 本章小节
本章的内容是第四章与第五章内容的延伸,在基于完成独立的卷积神经网络模型以及独立的长短期记忆网络模型后,尝试将两种模型相结合,利用卷积神经网络网络提取数据特征传给长短期记忆网络模型后进行处理,并产生最终模型,该网络模型的构建中,其标准化方法与前两者不同,这是为了能够让该模型达到比较优秀的预测效果,最后展示了通过CNN—LSTM模型对测试集数据的预测。
第7章 三种模型的对比
7.1 模型对比
7.1.1 主观分析
LSTM里的M就是Memory,所以LSTM主要的特点是有一定记忆能力,所以大部分时候是用来处理序列,比如处理一句话或者一段视频这样。CNN主要处理单张图的能力比较强,在一个序列里对前后的关联不太强。当两者集合时可以通过CNN来提取数据的特征信息,然后用LSTM处理,综上我认为虽然CNN-LSTM较两种单一的方法来说构造复杂,但是处理数据的能力更强。
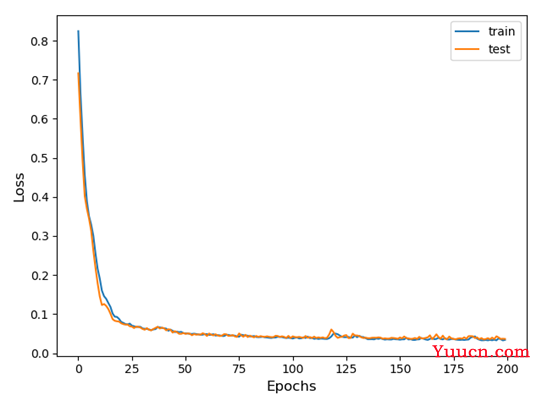
图7-1 CNN训练过程中Loss变化曲线
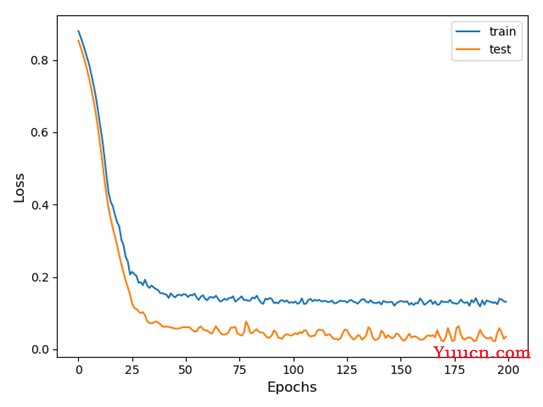
图7-2 LSTM训练过程中Loss变化曲线
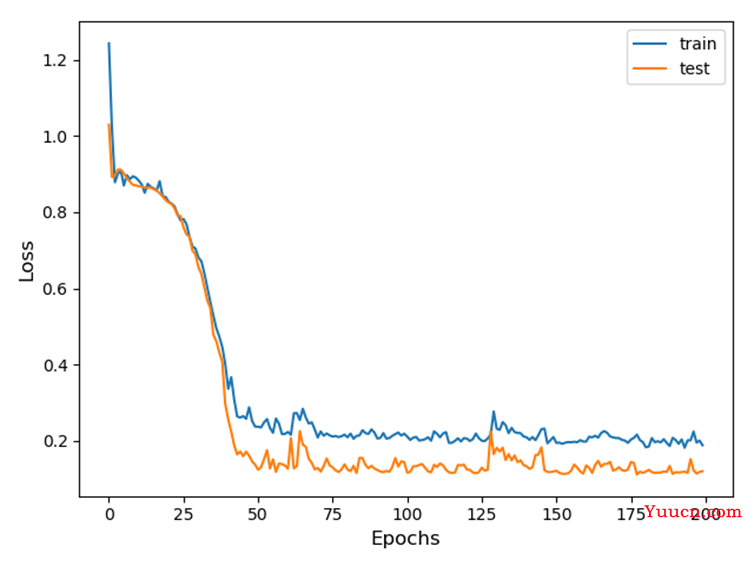
图7-3 CNN—LSTM训练过程中Loss变化曲线
观察上述两幅图像,CNN模型训练过程中损失下降更快,且更接近于0。而CNN-LSTM与单一的LSTM模型在损失下降到一定程度时表现基本一致,但有几点原因不可忽视,为了能够得到预测的数据使损失降低,CNN—LSTM的数据标准化方法不同,还有本次数据分析的样本数量不够庞大,对模型的训练也有一定程度的影响。
7.1.2 客观分析
|
CNN模型 |
LSTM模型 |
CNN—LSTM模型 |
|
|
MSE |
5952.12 |
68719.47 |
21535.56 |
|
RMSE |
77.15 |
40.96 |
146.75 |
|
MAE |
50.98 |
33.90 |
120.49 |
|
MAPE |
0.18 |
0.04 |
0.12 |
|
R2 |
0.99 |
0.99 |
0.98 |
MSE(均方差)是预测数据和原始数据对应点误差的平方和的均值
RMSE(均方根) 也叫回归系统的拟合标准差,是MSE的平方根
MAE平均绝对误差(Mean Absolute Error)范围[0,+∞),当预测值与真实值完全吻合时等于0,即完美模型;误差越大,该值越大。
MAPE平均绝对百分比误差(Mean Absolute Percentage Error)范围[0,+∞),MAPE 为0%表示完美模型,MAPE 大于 100 %则表示劣质模型
R2(R-Square)决定系数,判断模型的好坏,0表示拟合效果差,1表示模型无错误。
通过对比可以发现,在处理一维的数据时,LSTM模型的预测效果要比CNN模型的预测效果好,这是因为CNN主要用来处理的是图像,而当用其来处理一维数据的时候我将一维数据进行了reshape,使CNN模型能够间接的处理一维数据。
7.2 优化
为了保证实验的对比效果,三种模型均采用了相同的优化器adam优化器,采用该优化器的原因是,以往的随机梯度下降法学习速率单一,并且每一个模型参数都保持着一个学习速率。而在深度学习的领域,adam显著的优于其他的随机优化方法。其配置参数中的学习速率的大小可以确定学习的速度。其包含的自适应梯度对每一个不同的参数来调整不同的学习率,例如频繁变化则用小步长更新,稀疏的则用大步长更新。在本次设计中,数据的变化比较稀疏,为了利用稀疏梯度的信息,采用adam优化器,相比较于SGD算法其收敛的效果更好。
7.3 本章小节
本章的主要对比了三种以及搭建完毕的模型对测试集的测试效果,通过主观评价与客观评价进行分析。没有达到预期的效果的原因是训练集,以及标准化方法不统一。训练模型的数据不够庞大也是一方面。还有当卷积神经网络与长短期记忆网络结合时,数据类型的转换尤为关键,输出数据的类型也不相同,导致结果并未达到预期。