0 前言

前一段时间，想做一个文本相似性的系统，用于比对两个句子的相似性，因此接触了一下机器学习。其中主要是看李宏毅老师的机器学习视频课程。但是机器学习太过于复杂，对于我来说，我估计还没有入门，只是看到机器学习这个大殿。 这篇文章，是对我之前学习的一个总结，也是我对于机器学习的一个理解。如果大家要系统的学习，建议看一下李宏毅老师的机器学习课程视频。

1. 人工智能几个名词

人工智能是一个很广的词，它包含了机器学习、专家系统等。 但是到了现在，大家一般提到人工智能指的就是神经网络、机器学习了。就象伟人一样，机器学习也经历了“三起三落”：

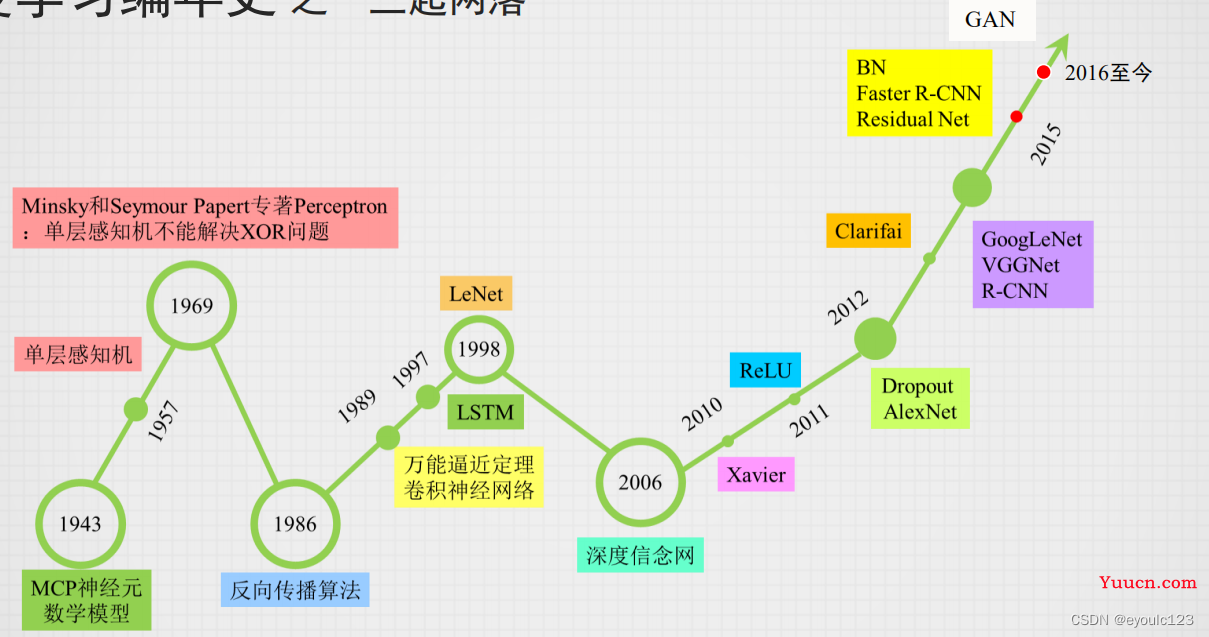
但是早期的时候，它并不是叫机器学习，而是以神经网络的名号来闯荡江湖。 但是随着XOR的问题提出，也宣判了神经网络的死刑。 在这后面很多年的时候，神经网络这个名声就开始变臭了，它的名声变臭到什么程度呢？只要文章中包含了“神经网络”这一个词，那篇文章就会被拒。 这怎么搞呢？没关系，给它再起一个名字，因此机器学习闪亮出场。

神经网络不是一个很新的技术，它出现的时间很早。 但是有一段时间，神经网络陷入了低谷，在这段时间，这个技术就变臭了，用台大李宏毅老师的话来说：神经网络象变成一个骂人的话，基本一有神经网络这个词，论文就会被拒绝。 后来随着技术的发展，人们发展神经网络还是可以解决很多问题的，但是“神经网络”这个词已经变臭了呀，这个时候人们又发明了一个新的词：机器学习。因此，我们可以这样子理解：机器学习 = 神经网络。

说完了机器学习与神经网络的关系，我们再具体说一下机器学习

2. 机器学习

总体来说，机器学习主要就是解决两个问题，或者说一个问题：回归问题。 对于回归，我不想讲解太多的内容。在这里，我们以一个简单的一元回归的问题，引入我们的分析。

2.1 一元线性回归问题

在我们中学的时候，我们经常会碰到这样子的一个例子。

例：
为了统计某地的房价，统计了平米数与房价

样本	房价（万件）	制造费用（万元）
1	60	100
2	70	120
3	72	121
4	80	140
5	90	160
根据以上数据，计算出产量与制造费用的关系

这个问题，就是一个典型的一元线性回归的问题。我们将制造费用设为y，而产量为x，那么我们就需要求出一个类似于$y = bx + a$的函数，即为：

在中学的时候，我们学过一元线性回归方程的计算公式：

最
小
二
乘
法
计
算
公
式
：
b
^
=
∑
i
=
1
n
(
x
i
−
x
ˉ
)
(
y
i
−
y
ˉ
)
∑
i
=
1
n
(
x
i
−
x
ˉ
)
2
a
^
=
y
ˉ
−
b
^
x
ˉ
\begin{aligned} & 最小二乘法计算公式：\\ & \hat{b} = \frac{\sum_{i=1}^{n}{(x_i-\bar{x})(y_i-\bar{y})}}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \\ & \hat{a} = \bar{y} - \hat{b}\bar{x} \end{aligned}
​最小二乘法计算公式：b=∑i=1n​(xi​−xˉ)2∑i=1n​(xi​−xˉ)(yi​−yˉ​)​a=yˉ​−bxˉ​
那么上面的结果我们就可这样子计算出来：

1. 计算平均值

x
ˉ
=
60
+
70
+
72
+
80
+
90
5
=
74.4
y
ˉ
=
100
+
120
+
121
+
140
+
160
5
=
128.2
\begin{aligned} & \bar{x} = \frac{60+70+72+80+90}{5} = 74.4 \\ & \bar{y} = \frac{100+120+121+140+160}{5} = 128.2 \end{aligned}
​xˉ=560+70+72+80+90​=74.4yˉ​=5100+120+121+140+160​=128.2​
3. 带入
b
ˉ
\bar{b}
bˉ公式计算

b
^
=
(
60
−
74.4
)
(
100
−
128.2
)
+
(
70
−
74.3
)
(
120
−
128.2
)
+
(
72
−
74.4
)
(
121
−
128.2
)
+
(
80
−
74.4
)
(
140
−
128.2
)
+
(
90
−
74.4
)
(
160
−
128.2
)
(
60
−
74.4
)
2
+
(
70
−
74.3
)
2
+
(
72
−
74.4
)
2
+
(
80
−
74.4
)
2
+
(
90
−
74.4
)
2
=
2.014
\hat{b} = \frac{(60-74.4)(100-128.2) + (70-74.3)(120-128.2) + (72-74.4)(121-128.2)+ (80-74.4)(140-128.2) + (90-74.4)(160-128.2)}{(60-74.4)^2 + (70-74.3)^2 + (72-74.4)^2 + (80-74.4)^2 +(90-74.4)^2} = 2.014
b=(60−74.4)2+(70−74.3)2+(72−74.4)2+(80−74.4)2+(90−74.4)2(60−74.4)(100−128.2)+(70−74.3)(120−128.2)+(72−74.4)(121−128.2)+(80−74.4)(140−128.2)+(90−74.4)(160−128.2)​=2.014
4. 计算
a
ˉ
\bar{a}
aˉ：

a
ˉ
=
y
ˉ
−
b
^
x
ˉ
=
128.2
−
2.014
∗
74.4
=
−
21.641
\bar{a} = \bar{y} - \hat{b}\bar{x} = 128.2- 2.014*74.4 = -21.641
aˉ=yˉ​−bxˉ=128.2−2.014∗74.4=−21.641

4. 写出方程：
   y
   ^
   =
   2.014
   x
   ^
   −
   21.641
   \hat{y} = 2.014\hat{x} -21.641
   y​=2.014x−21.641

这个计算过程，是我们以前的方法，但是对于从事计算机的人员来说，这种优雅的方式，不是我们的风格。我们崇尚的“暴力出奇迹”，充分利用计算机的计算能力，随便给定一个a和b，然后不断的逼近它，使得它们的值最小。例如我让a = 1, b =1,然后，我们看结果：

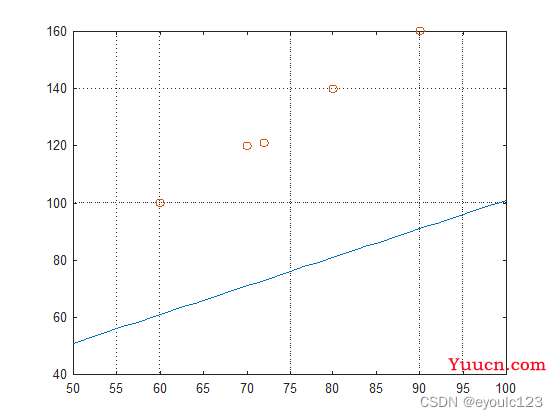
从上面的图中，我们就可以看到a和b的值不合理，我们需要将整条直接往上移一下，然后尝试改变a的值，同时斜率也感觉不符合相求，最后不断的变化，直接到找到一个符合我们要求的值。

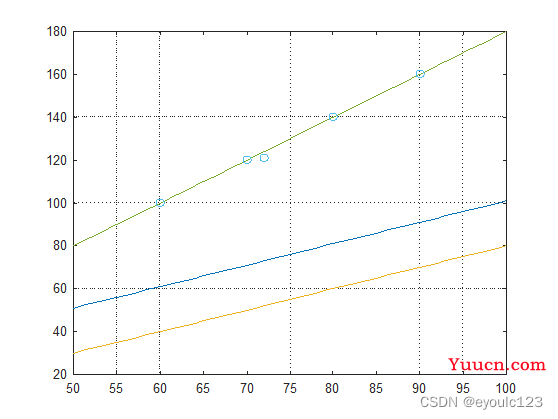
至我们如何判断a与b的值是否合适，这里就涉及到一个处理方式：梯度下降的方法。大家只需要知道，有一个固定的方法，通过这个固定的方法，我们可以知道对应的a与b是往大调，还是往小调。 通过这种方法，我们不断的逼近我们的散点。最终得到一个符合我们要求的方式。

最终的函数，我们可以得到一个，当我们输入的x = 5时，我们就会发现一个问题 房价为-1.5，房价不可能为负值。因此一般在最后的输出的时候，增加一个修改函数。 整体就变成了：

其实这个修改函数，有一个专业的名词：激活函数（不知道它为啥叫激活函数，但是我一直感觉它的作用就是对结果值进行修正。后面我们也称它为激活函数）。常用的也只有几个。一个叫ReLU函数，一个是Sigmod函数。 下面是它们两个的函数图形。如果懒得看，可以直接跳过。 我们只需要记住，它们的作用就是对于预测函数的数值进行一个修改，让它更靠谱一些。

ReLU函数：

Sigmod函数：

在上面的那个例子中，我们只有一个输入，就是房子的大小，即平米数。但是我们都知道房价并不只是与大小相关，还与位置、房型相关等其它因素相关。因此我们还需要将这些东西。我们假设位置为变量x1, 房型为x2参数，而每一种因素，我们都可以表示成一个类似于$y=bx +a$形式的方程，那么房价表示，可能就需要为：

总
房
价
=
(
房
屋
大
小
因
素
x
)
+
(
位
置
因
素
x
1
)
+
(
房
型
x
2
)
y
=
(
b
x
+
a
)
+
(
b
1
x
1
+
a
1
)
+
(
b
2
x
2
+
a
2
)
总房价 = (房屋大小因素x) + (位置因素 x1) + (房型 x2) \\ y = (bx + a) + (b_1x_1 +a_1) + (b_2x_2 + a_2)
总房价=(房屋大小因素x)+(位置因素x1)+(房型x2)y=(bx+a)+(b1​x1​+a1​)+(b2​x2​+a2​)

我们将它画成图，就可以看到：

这个图再整理一下，就变成了我们经常看到的很复杂的一个图。 这里再总结一下，其实对于整个神经网络而言，它都是在做一个事情，就是解一个类似于y = bx + a的一元线性方程。只不过复杂的神经网络，都是在解决很多个一元线性方程。

2.2 逻辑回归

对于房子来说，获取一个预测的价格是一个因素，但是大家可能更希望的是知道这个房子值不值得买？那值不值得买，其实就是一个概率。 这就是一个二分类的问题。值或不值，两种可能。 事实上，机器学习处理的绝大多数问题都是一个分类问题，只不过这种分类的规模的大小问题。 如动物识别，分类的规模就是全部动物的种类；NLP语言处理的分类规模就是整个词语库，如汉语是6000个，那这个分类规模就是6000种；下围棋AlphaGo 的分类则是棋盘大小 – 19*19(事实没有这么大)。

事实上机器学习处理的绝大多数东西都是逻辑回归的问题。针对逻辑回归，也有一大批的数学支持。大家只需要只需要记住一点：机器学习更多的是解决分类问题。

3. 机器学习的几个名词

上面讲完了机器学习的处理问题，下面我们接着来说一下，常见的几个名词。

3.1. 神经元与神经网络

在上面的房价例子中，那个一元线性函数+ 修改函数组合在一起，就是一个神经元。

但是一般来说，大家觉得这样子画得太复杂了，那么就把神经元简单画成一个小圆圈，结果就变成了：

单个看这个，好象没有什么感觉，如果我们把上面的房价的图形变一下，那就会变成如下常见的那种样子。

事实上，有的时候，大小、位置、房型它们都是相互牵连的。然后这个图就变成：

但是此时有人会想，我为啥不能在y1,y2,y3再叠加几层呢？这样子说不定效果更好。结果他们是对的，效果好象更好。其架构图就变成这样子了：

在这里大家可能会有一个问题：我们怎么知道需要加多少层，输入之间如何连线呢？ 答案是不知道。 谁也不知道要叠多少层，谁与谁连。 这就有点儿象古代的炼丹术士

他们在炼丹的时候，也不知道会出来什么，只知道把几个东西放在炉子里，然后加火烧，出来什么就看天了。 如果炼出来好东西来了，就把记下来，大家就按这个顺序来搞。如果不行，就不断的试。最后就炼出了元素周期表这种可以指导炼丹的东西出来。

现在的机器学习一样，感觉就是古代的炼丹术一样，大家都不知道能够炼出来啥，很多时候都是看天。现在很多人把机器学习说成炼丹。 以后了可能会出现类似于元素周期表这一种统一指导大家。但是现在大家需要知道的是，已经有牛人炼制好一些丹药，大家后面就按照这种方式来搞就好了。

3.2 损失函数

虽说我们称机器学习为炼丹。但是这个“丹”好不好，还是有一些判定方法。这个就是损失函数。

我们还是以上面的平米数与房价的一元回归函数为例，进行说明。 我们之前说过，计算机信奉“大力出奇迹”，所以它就是随便设定一个函数，例如直接给出y = x + 1， 但这个函数准不准呢？我们就可以利用计算值与真实值的偏差，如果这个偏差很大，那肯定就不对，如果这个偏差差的不大，那我们就可以接受。

事实上，关于损失函数，有很多计算方式。大家只用记住一点，损失函数就是度量我们最后结果好坏的，如果这个损失函数结果很小，在可接受的范围内，那么就证明我们的机器学习计算出来的结果很好；如果这个结果很大，我们不可接受，那我们就还需要继续调整参数，然后再次判断。

当这个损失函数结果，我们不能接受，我们就需要调整一元函数的两个参数，那么是应该往大调还是往小调呢？这个指导的方式，就是梯度下降。

3.3 梯度下降

梯度是我们大学学过的一个概念，其实就是就是求导。 其中有一个关于导数的意义，需要特别提一下。 那就是导数是变化率、是切线的斜率。 从下图中，我们可以看到，当曲线越平滑的时候，切线的斜率越小。

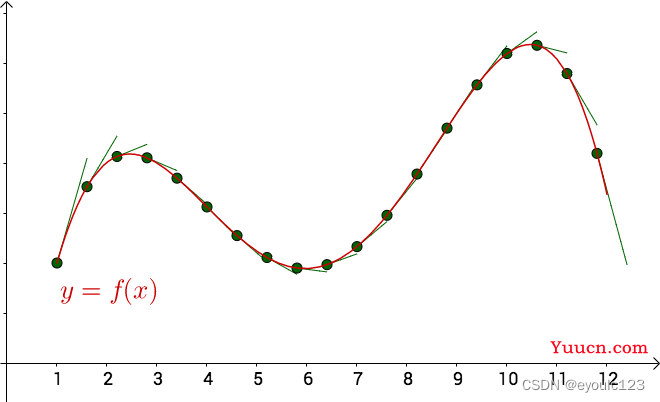
而梯度下降就是查看损失函数的斜率，如果损失函灵敏的斜率是正，则往左偏一点，如果斜率为负，则往右偏一点。如果斜率为0了，则表示它已经到了它能够到达的最低点，也就达到我们的要求。 整个炼丹结束了。 这样子说可能还是有点儿抽象。 我们再结合上面的损失函数，来看看。

3.4 过似合、欠似合

上面我们说了，我们是函数是根据我们的数据值来进行计算的。但是这个计算的结果可能不是很准。还是以我们的函数，为例：

样本	房价（万件）	制造费用（万元）
1	60	100
2	70	120
3	72	121
4	80	140
5	90	160

如果我们给定这样子的一个函数：

y
=
{
100
,
当
x
=
60
120
,
当
x
=
70
121
,
当
x
=
72
140
,
当
x
=
80
160
,
当
x
=
90
1000
，
其
它
y=\left\{ \begin{matrix} 100, 当x = 60 \\ 120, 当x = 70 \\ 121, 当x = 72 \\ 140, 当x = 80 \\ 160, 当x = 90 \\ 1000，其它 \end{matrix} \right.
y=⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧​100,当x=60120,当x=70121,当x=72140,当x=80160,当x=901000，其它​

对于这个函数，我们的每个值都运行很好。但是实际用它来预测房价呢？肯定是一个都不对。这种在我们训练的时候，表现的很好，但是在实际使用中一塌糊涂的模型，我们就称它为过似合。

与之相对的，就是在我们训练集中，都表现的不好，我们就称为欠似合一样。

就象小孩上学，如果平时做练习题的时候，都表现得很差，错误一大批，我们就说这个小孩“欠揍”、“欠练习”，日常作业都做不好；而如果一个小孩每天做大量练习题，但都是很机械的做题，完全不理解题，那我们看到的就是作业做的很好。但是期末考试的时候，题目都没有见过，我们就会说这个小孩平时习题“过量”、缺少思考。

事实上，学校老师也知道，作业多了不行，少了也不行。 因此，老师会将平时的习题分为两个部分：一部分发给小孩平时练习，还有一些则是做单元测试。

而在我们机器学习的训练过程中，也是一样，会将数据集分为训练集与测试集。

4. 现阶段常见的神经网络

正如我们在前面说过的，机器学习现阶段还处于一个远古炼丹术阶段。 没有一个纲领性的理论进行指导。 现有的成果都是一群大佬的经验总结。对于我们这些“炼丹学徒”来说，我们学习这些大佬们的成果，然后应用好这些成果。 下面是一种总结（以台大李宏毅老师的机器学习的网络课程为术，这里只有三种网络，还有Self attention\bert\GAN 我自己学得也不是太清楚，所以没有展开说明。反正这篇文章的目的，只是一个机器学习的入门介绍。）

4.1 向量化

我们都知道计算机只能处理一些数值类型的数据，所有的东西我们都是转换成01之类的二进制数值来处理。但是我们人类平时阅读的文字、说话的语音还有看的图片，这些不是数字，那应该怎么处理呢？

1. 图片处理

图像是最容易向量化的。 我们知道，我们的是通过RGB来表示色彩的。 而一般来说，一个图片，也是由R、G、B这三种。下面这个图是吴恩达讲程中的一个图

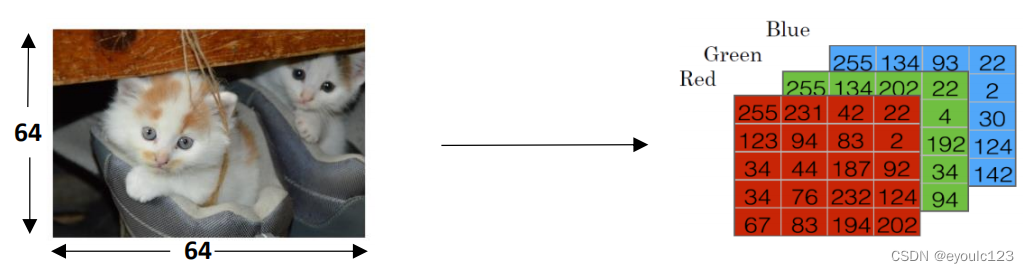
从上面可以看到图片在计算机中本来就是以数字的方式存储的

2. 文字处理

文字需要进行数值化处理最简单最容易想到的一种方式就是：给每个词一个编号，然后将句子转成编号。 事实上，大家也是这样子处理的，只不过它有一个比较高级的名字：one-hot（事实，one-hot已经不再使用，但是它最好理解）。只不过使用one-hot进行编码，是通过向量的方式。对于中文来说，我们常用的词语极其是有限制的，大约只有6000多个词。6000个词这个量太大，在这里不好举例表示。假设我们现在有一个词典库，这个词典库只有如下几个词：

我 、你、吃、打、球、 饭

那么我们对应的一个词向量词典：

我： 1 0 0 0 0 0
你： 0 1 0 0 0 0 
吃： 0 0 1 0 0 0
打： 0 0 0 1 0 0 
球： 0 0 0 0 1 0
饭： 0 0 0 0 0 1

我们表示“我吃饭”，我们就可以这样子向量化：
你打球， 那么我们就可以将这句话有如下的一个数值表示：

      我|你|吃|打|球|饭
你：  0  1  0  0  0  0
打：  0  0  0  1  0  0
球：  0  0  0  0  1  0

按照上面的例子，“你打球”这句话对应的数值为：

{你打球} = \begin{Bmatrix}
0 & 0 & 0 \\ 
1 & 0 & 0 \\ 
0 & 0 & 0\\ 
0 & 1  &0 \\ 
0 & 0 & 1\\ 
0 & 0 & 0
\end{Bmatrix}

通过这种方式，我们就把文字转成数字了。

3. 语音处理

最后我们说一下语音的处理。语音处理则是将一段音频文件，按时间进行切割，然后每25ms为一小段，这一段小段就应一个数据的输入。 放一张李宏毅老师的讲课截图。

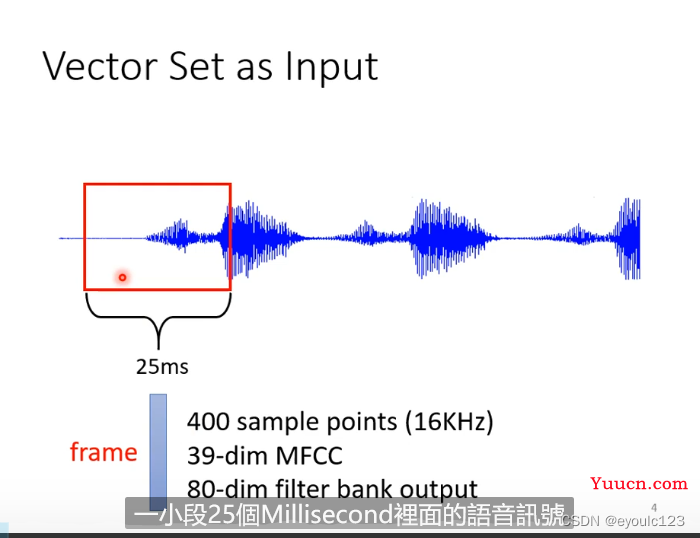
其中的文字部分则是它的处理方式（这一段，没有讲，我也没有研究过）

4.2 全连接神经网络

其实现阶段，使用全连接神经网络的已经很少。但是个人感觉全连接神经网络是最容易
其实全神经网络并不是一个什么处理方式，但是我个人觉得，但是这个更好理解。后面的诸多模型，都是在在这个基础上进行改进。

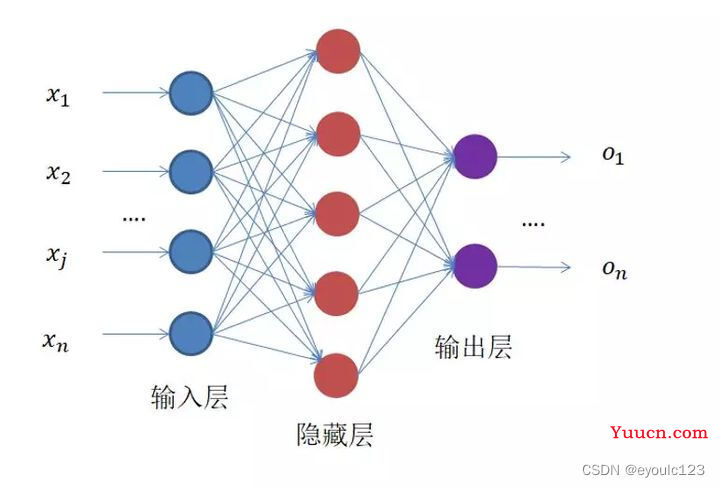
从图中，我们可以看到，我们的输入是(x1, …, xn)，每个输入、每个神经元都会连接。 这种情况就称为全连接。 全连接神经网络，就感觉象是，我也不知道这些输入是什么关系，但是我感觉这些输入它们是相互关联，那我就把它们都关联起来吧。

我们还是以吴恩达教授在课堂上举的那个例子进行说明。 我们有一个图：

其中左边是我们的这张图在计算机器中存储的数据。那么，我们首先要做一件事，就是把这个图拉直，什么叫拉直呢？就是将所有的数据都写在一列。 首先，我们把红色拉平：

然后再次绿色拉平：

再次蓝色拉平

最后我们把我们拉直后的红、绿、蓝的三个向量叠在一起，那么我们的图片输入到神经网络中的向量就是：

我们实际处理的向量也是这种一维向量了。 事实上，我们的所有的神经网络处理的向量都是这种一维向量。也就是所有的输入都是经过拉直处理后的一维向量。 而我们的输入也是一层一层的传递下去。 就象我们常见的接力搬砖一样

小朋友们排成一队，然后一起去搬砖。那这一列小朋友就组成了一个神经网络（只不过他们只有向量只有一个，是一个一维向量），每个小朋友就是一个神经元。输入就是我们需要搬运的东西。第一个小朋友把搬运的东西拿起来，然后递给下一个，一层一层的传下去，最后传到目的地，假设最后一个目的地是一位老师。 老师拿到手里一看，这个是啥呀？这根本不是砖，是个没用的垃圾。老师肯定就会跟自己前面的一位同学说：注意一点，别把垃圾传递过来了， 这位同学又跟自己前一位同学也说注意点。这样子一层一层的往前传过去。 这种传播方式就是反向传播了。

如果我们这里需要传送不是一块砖，是一个信息。每个人都需要根据前一个人的输入，做一点判断，然后传给下一个人。最后那个人，说最终结果。 有点儿像《王牌对王牌》的传声筒游戏。

当时看的时候，大家可能被结果逗得捧腹大笑，特别是最后复盘的时候。 其实复盘的时候，就是一个反向传播的典型例子。 最后一个人回答错了，他说会说，我前面你比的是一个啥呀。然后前面那个人说我是根据我前面一个人传过来的意思，然后比划的，这个传递消息的方式，我们可以理解成一个上一个输入通过一个函数后，输出一个结果。 最后一个人可能会说，你不能这样子呀，你要换一种方式呀。这个换一种方式就是一个参数调用。 然后这样子一层一层的回传到最前面。

我有一段时间比较喜欢看这个节目，我发现一个现象，就是王牌家族，他们在一起的时间更长，更容易获胜一些。 这换成我们机器学习的语言就是：他们经过了训练数据更多，他们的参数已经经过了多次调优了，因此他们的准确性更高一些。

4.3 卷积神经网络 CNN

在全连接神经网络中，我们将整张图片的数据都给到网络中进行计算了。 事实上，很多时候，我们并不必要处理所有的数据。就象我们看一张图片，我们只需要看一下局部就知道这个东西是啥了，并不是把整张图片都看完。 如果我们在神经网络中，我们只处理局部的数据，那么会大大的减少我们的计算量。极大的提升整个系统的计算性能。

以李宏毅老师课程中的例子进行说明。

假设我们按照我们的经验，我们总结三个经验：看一下鸟嘴是不是尖的， 看一下鸟眼睛是不是小而圆的，看一下爪子形状。然后我们针对这三个特性，写出三个函数，每个函数对应一条规则。然后我们把鸟嘴那一小块图片给鸟嘴规则去处理；鸟眼图片则交给鸟眼规则来处理。

这样子，我们可以通过切块的方式来实现计算数据量的减少，这种方式叫做Convolution。 事实上，这并不是唯一的处理方式。 喜欢照相的同学可能都知道，不同相机照出来的相片大小，可能相差很远。有一些相片，可能有10多M，有一些相片可能只有几百K。这些几百K的相片，会影响我们对于内容的识别吗？答案肯定是不会。 CNN也会利用这种方式来进行处理：

上面是将左图中的数据，间隔抽取，然后就变成了右图。 这种抽取方式也有一个专门的名词，叫做pooling。 李宏毅老师最后也给出了一个常见的CNN的网络架构。 大家可以参考一下。

4.4 RNN

每天早上，我都需要送小孩去上学。但是每天早上穿什么衣服，就是一个比较头疼的事情。 如果有这样子的一个服务，这个服务告诉我每天都需要早上要穿什么衣服就好了。当然，并没有这样子一个服务，更多的时候，都是孩子妈妈告诉我早上穿什么衣服。那我们是否能够开发一个妈妈式的人工智能来处理这个事情呢？我们不妨来分析一下妈妈是根据什么东西来判断今天穿什么衣服的

• 今天的气温
• 会不会出太阳
• 今天是不是星期一，学校的要求
• 昨天穿的是什么。

今天气温是26度， 有太阳，学校也没有啥特殊要求。而且昨天就是穿的短袖，但是有点儿冷。那今天就穿长袖吧。 我们将这个过程画出来:

在这个系统中，我们有一个很重要的输入，就是需要考虑之前的结果。今天我预测出来穿长袖，然后我们继续预测明天穿什么的时候，我们就将今天的输出结果做为输入，参与预测； 在预测后天的时候，我们就将明天的预测结果作为输入。 按照这种方式，我们就可以一直预测下去。

这种前一个状态参与后一个状态值的预测的方式，我们就称为RNN。

5. GPU

在最后，我想再说一下GPU的问题。我们每次提到了机器学习都会提到GPU。好象如果需要机器学习的地方，就一定需要GPU。 这其实是一种误解。 其实很多时候，如果机器学习的模型已经训练好了，我们根本用不到GPU的算力。 那为什么我们每次提到机器学习就说需要GPU呢？

这可以从几个方面来说。 我们首先说一下机器学习中大量存在的矩阵计算。 机器学习大量处理的就是矩阵运算。而GPU在这一块有很大的优势。

2.1 SIMD与CUDA

在介绍GPU之前，我们首先提到一个名词 – SIMD（单指令多数据流）。这个是啥意思呢？其实，我们在很小时候，就使用过SIMD这个东西。

这种抄作业的方式，应该很多都经历过吧。这就是一个SIMD的典型应用。写的动作只有做一次，但是可以写出几行数据来。SIMD的核心思想就是一条指令，处理多行数据。 但是我们注意没有，我们用多次笔抄作业的时候，写出来的数据都是一样的，绝对不会出来，第一支笔写一个字，第二支笔写出来的却是另外一个字。 这就是SIMD的一个限制，使用SIMD来处理的时候，处理的方式需要一样。假如，我们希望一次性的把这三个都算出来：

$$1+2=？2\ast 3=？3+2=？$$
这是绝对不可能，因为SIMD不能一个处理 加法，一个处理减法。 现阶段有一个很火的数据库系统 clickhouse，它的速度之所以能够比其它的数据库的主要原因，就是因为他使用了SIMD。

需要注意的是SIMD这个是CPU提供的。那SIMD和CUDA有啥关系呢？ 我们可以这样理解，GPU实现了SIMD，其中专门用来计算的指令单元就是CUDA。 这样子说可能会比较抽象，我们举个例子，大家就清楚了。

我们现在有一个叫GF的人力资源公司。很多公司会将一些脏活、累活、不用动脑子的工作外包给这个公司来处理。 这个公司也比较大，有500个人。 某个公司每年年底的时候都需要统计一下这一年某一天相对于上一年的这一天销量上涨情况。 以往，他们都是派几个员工，分开计算。一年有365天，就是365个数据相减，工作无聊。 自有员工很无聊，大家都不愿意干。最后他们将这个活外包给这个GF公司。这种简单的活，就最适合于GF这种公司，每个员工的人力成本低，而且他们最会做这种集体运算。他们拿到活之后

有这样的一个公司，这个公司每年年底的时候，都需要统计一下这一年某一天相对于上一年的这一天销量对比情况。以往的时候，都他们自有员工来干这个活，工作简单、枯燥。员工在干这个活的时候，都不能做其它的事情，而且自有员工工资一般都会比较高。这个损耗太大了。 这个时候，有一个GF的人力资源公司说，你们把这个简单的活派给我来做吧，我现在养了500个小弟，但是这些小弟，小时家里穷，小学都没有毕业就开始干活了，所以只能做一些简单的加减乘运算。 你们这种销量对比的活，可以给我来做。 然后这个公司就把两个账本，通过快递送过来，GF公司拿到这两个账本之后，就对自己的小弟们来，你们来365个人，来把这个计算一下。计算之后的结果再告诉我。

GF公司里面干活的这些小弟，就是一个CUDA，他们没读过什么书，所以复杂的逻辑判断，你就不要指望它来做的。 而C公司就是CPU，因为它是通用计算的，因此，他里面的计算核心相对来说会贵一些，而且它能够处理很多复杂的逻辑。 但是有一个问题，如果GF公司还没有计算完成，这个时候C公司又说，我还有一批活，你也帮我处理一下，然后一把扔过来。这个时候，GF公司就傻了，我上个还没有弄完，你现在又给我一个，我完全弄混了。 这个就是“显存污染”。 事实上CPU与GPU之间是通过高速的PCI连接，我记得看过一个介绍，它们之间可以达到40GB/秒，因此传输速度大家就完全不用关注了。

从上面例子中，我们可以看到，GF这个公司小弟越多，那么它干起活来越快。因此，我们看现在越是贵的N卡，CUDA个数越多，这就是这个道理。

6. 参考资料

1. 李宏毅 台湾大学 机器学习视频 https://www.bilibili.com/video/BV1Wv411h7kN?p=23
2. 深度学习开端｜全连接神经网络 https://zhuanlan.zhihu.com/p/104576756
3. 深度学习基础课程 https://study.163.com/course/introduction/1005023019.htm