上周末梳理了NeurlPS'22中推荐系统相关论文,详见NeurlPS'22 推荐系统论文梳理。本想精读其中某篇,但是并没有公开。最近知乎刷到很多ICLR'23的总结文章,我把他们汇总在ICLR'23 论文整理合辑一文中,含扩散模型、图网络、推荐系统、强化学习、知识蒸馏、NLP等多个方向。
本文对其中的推荐系统论文 Simple Yet Effective Graph Contrastive Learning for Recommendation 一文进行解读。论文可在公众号后台回复 ICLR-2023-RecSys 获取,所有论文都是按照该方式存档。 本文代码也已公开在https://anonymous.4open.science/r/LightGCL/。
论文摘要
大多数现有的图对比学习方法要么在用户-项目交互图上执行随机增强 (例如节点/边扰动,node/edge perturbation),要么依赖基于启发式的增强技术 (例如用户聚类)来生成对比视图。我们认为这些方法不能很好地保留内在的语义结构,并且容易受到噪声扰动的影响。
本文提出了一种简单而有效的图对比学习范式 LightGCL,以缓解那些对基于对比学习的推荐器的通用性和鲁棒性产生负面影响的问题。我们的模型专门利用奇异值分解 (SVD,singular value decomposition)进行对比增强,从而通过全局协作关系建模 (global collaborative relation modeling)实现无约束的结构细化 (unconstrained structure refinement)。在几个基准数据集上进行的实验表明,我们的方法显着提高了现有技术的性能。进一步的分析表明 LightGCL在数据稀疏和流行度偏差的鲁棒性方面的优越性。
研究动机
图神经网络通过聚合邻居表示提取局部协同信号,在基于图的推荐系统中展示出优越的效果。大多数基于 GNN 的协同过滤模型都遵循监督学习范式,然而,实际推荐场景中,在有限的交互数据中学习高质量的用户和项目表示时会面临数据稀疏问题。因此,对比学习被引入推荐任务以进行数据增强。
当前大多数图对比学习 (GCL)方法采用基于启发式的对比视图生成器来最大化输入正对之间的互信息并推开负例。为了构建扰动视图,SGL通过使用随机增强策略 (例如节点丢弃和边扰动)破坏用户-项目交互图的结构信息来生成正视图的节点对。SimGCL提供了带有随机噪声扰动的嵌入增强。为了识别节点 (用户和项目)的语义邻居, HCCF和NCL追求图结构相邻节点和语义邻居之间的一致表示。
尽管它们很有效,但最先进的对比学习推荐系统仍存在几个固有的局限性:i) 带有随机扰动的图增强可能会丢失有用的结构信息,从而误导对比表示学习; ii) 启发式引导表示对比方案的成功很大程度上建立在视图生成器上,这限制了模型的通用性并且容易受到嘈杂的用户行为数据的影响; iii)当前大多数基于GNN的对比推荐器都受到无法区分表示的过平滑问题的限制。
鉴于上述限制和挑战,本文提出简单而有效的增强方法 LightGCL 重新审视图对比学习范式进行推荐。 在该模型中,图增强由奇异值分解 (SVD) 指导,不仅提炼用户-项目交互的有用信息,而且还将全局协作上下文注入对比学习的表示对齐中。 强大的图对比学习范式可以很好地保留用户-项目交互的重要语义,而不是生成两个手工制作的增强视图,这使我们的自增强表示 (self-augmented representations)能够反映用户独特的偏好和跨用户的全局依赖关系。
研究方法
本文提出的LightGCL 是一种轻量级的图对比学习范式,如图 1 所示,它通过全局协作关系增强来增强图对比学习,以实现有效的用户表示。

局部图依赖建模 (Local Graph Dependency Modeling)
每个用户u_i和商品v_j,其embedding向量是e_{i}^{(u)},e_{j}^{(v)}\in R^{d} ,d是embedding的维度。所有用户和商品embeddings的集合定义为E^{(u)}\in R^{I\times d} ,E^{(v)}\in R^{J\times d} ,I和J分别是用户和商品的数量。参考[1],作者使用两层的GCN来聚合每个节点的邻居信息。在l层,聚合过程如公式 (1) 所示:

其中z_{i,l}^{(u)}和z_{j,l}^{(v)}表示用户u_i和商品v_j在第l层聚合的embedding. \sigma (\cdot )是LeakyReLU激活函数,negative slope是0.5. \tilde{\mathcal{A}}是标准化的邻接矩阵,对其进行edge dropout (表示为p (\cdot )) 以缓解过拟合问题。作者在每一层实现残差连接以保留节点的原始信息,如公式 (2) 所示:

节点的最终embedding是其在所有层中embedding的总和,用户u_i和商品v_j的最终embedding之间的内积预测u_i对v_j的偏好,如公式 (3) 所示:

高效全局协同关系学习 (Efficient Global Collaborative Relation Learning)
为了通过全局结构学习增强推荐图对比学习,LightGCL使用奇异值分解,以从全局视角有效地提取重要的协同信号。 具体来说,我们首先对邻接矩阵\mathcal{A}使用奇异值分解,得到\mathcal{A}=\mathcal{U}\mathcal{S}\mathcal{V^{\top}},U / V 是一个 I ×I / J ×J 正交矩阵,其列是 A 的行-行/列-列相关矩阵的特征向量。 S 是存储 A 的奇异值的 I ×J 对角矩阵。最大的奇异值通常与矩阵的主成分相关联。 因此,我们截断奇异值列表以保持最大的 q 值,并用截断矩阵重构邻接矩阵\mathcal{\hat A}=\mathcal{U_{q}}\mathcal{S_{q}}\mathcal{V_{q}^{\top}}
,其中 \mathcal{\hat U_{q}}\in R^{I\times q} 和\mathcal{V_{q}}\in R^{J\times q} 分别包含U 和 V的第一个q列。 \mathcal{S_{q}}\in R^{q\times q}是 q 个最大奇异值的对角矩阵。
重构矩阵\mathcal{\hat A}是邻接矩阵\mathcal{A}的低秩近似,因为它保持rank(\mathcal{\hat A}) = q. 基于SVD的图结构学习有两方面优势:首先,它通过识别对用户偏好表示重要且可靠的用户-项目交互来强调图的主要部分;其次,生成的新图结构通过考虑每个用户-项目对来保留全局协同信号。 给定\mathcal{\hat A},我们在每一层重建的用户-项目关系图上进行消息传播:

然而,在大规模矩阵上执行精确的奇异值分解非常昂贵,这使得处理大规模用户-项目矩阵变得不切实际。 因此,我们采用[2]中提出的随机 SVD 算法,其关键思想是首先用低秩正交矩阵逼近输入矩阵的范围,然后在这个较小的矩阵上执行 SVD。

其中 q 是分解后的矩阵所需的秩, \mathcal{\hat U_{q}}\in R^{I\times q},
\mathcal{\hat S_{q}}\in R^{q\times q},
\mathcal{\hat V_{q}}\in R^{J\times q} 是\mathcal{U_{q}},\mathcal{S_{q}},\mathcal{V_{q}} 的近似。 因此,我们使用近似矩阵和embedding的整体表示重写公式 (4) 中的消息传播规则,如下所示:

其中G_{l}^{(u)} 和G_{l}^{(v)}是从新生成的图结构视图编码的用户和商品embedding的集合。 我们可以存储低维的 \mathcal{\hat U_{q}},
\mathcal{\hat S_{q}},
\mathcal{\hat V_{q}},而无需计算和存储大的密集矩阵\mathcal{\hat A}_{\mathcal{SVD}}。通过在数据预处理阶段用近似 SVD 预先计算 (\mathcal{\hat U_{q}}
\mathcal{\hat S_{q}}) 和 (\mathcal{\hat V_{q}}
\mathcal{\hat S_{q}}),可以提高模型效率。
简化的局部-全局对比学习 (Simplified Local-Global Contrastive Learning)
传统的 GCL 方法,例如 SGL 和 SimGCL 通过构建两个额外的视图来对比节点embeddings,而从原始图 (主视图)生成的embeddings不直接参与 InfoNCE loss。采用这种繁琐的三视图范式的原因可能是用于增强图的随机扰动可能会给主视图embeddings提供误导性信号。在我们提出的方法中,新生成的图视图是在保留全局协同关系的情况下创建的,这可以抵抗数据噪声和不完整性,以增强用户表示。因此,我们通过直接对比SVD增强的视图embeddings g_{i,l}^{(u)}与 InfoNCE 损失中的主视图embeddings z_{i,l}^{(u)}来简化对比学习框架:

其中 s(·) 和 τ 分别表示余弦相似度和温度系数。商品的InfoNCE损失L^{(v)}_{s}以相同的方式定义。为了防止过拟合,我们在每个batch中实现了一个随机节点dropout,以排除一些节点参与对比学习。 如公式 (8) 所示,对比损失与我们的主目标函数联合优化:
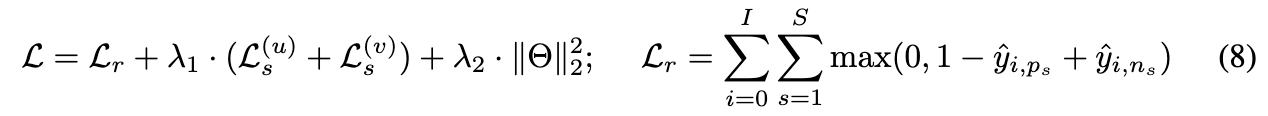
实验结果
实验部分主要是回答以下5个问题:
- 与各种 SOTA 基线相比,LightGCL 在不同数据集上的表现如何?
- 轻量级图对比学习如何提高模型效率?
- 我们的模型在数据稀疏、流行度偏差和过平滑方面表现如何?
- 局部-全局对比学习对我们模型的性能有何贡献?
- 不同的参数设置如何影响我们的模型性能?
实验设置
作者在五个真实世界数据集上评估模型和基线:
- Yelp (29,601个用户,24,734个项目,1,517,326个交互) : 从 Yelp 平台上的评分交互中收集的数据集;
- Gowalla (50,821个用户,57,440个项目,1,069,128次交互) : 包含从 Gowalla 平台收集的用户签到记录的数据集;
- ML-10M (69,878个用户,10,195个项目,9,988,816次交互) : 用于协同过滤的著名电影评分数据集;
- Amazon-book (78,578个用户,77,801个项目,3,190,224次交互) : 由用户对从亚马逊收集的书籍的评分组成的数据集;
- 天猫 (47,939名用户,41,390件商品,2,357,450次互动) : 一个电子商务数据集,包含用户在天猫平台上不同产品的购买记录。
作者将数据集分为训练集、验证集和测试集,比例为 7:2:1;采用 Recall@N 和NDCG@N,其中 N = {20, 40} 作为评估指标。
Baseline方法包括:
- MLP增强的协同过滤:NCF
- 基于GNN的协同过滤:GCCF、LightGCN
- 解耦图协同过滤:DGCF
- 基于超图的协同过滤:HyRec
- 自监督学习推荐系统:MHCN、SGL、HCCF、SHT、SimGCL。
RQ1:性能验证
- 对比学习主导:对比学习类方法取得更好的效果,这可能归因于对比学习 学习均匀分布的embedding的有效性[3]。
- 对比学习增强:我们的方法始终优于所有对比学习基线。 我们将这种性能改进归因于通过注入全局协同上下文信号来有效增强图对比学习。 其他基于对比学习的推荐器(例如,SGL、SimGCL 和 HCCF)很容易受到嘈杂的交互信息的影响,并产生误导性的自监督信号。

RQ2:效率研究
由于额外视图的构建和训练期间对它们执行的卷积操作,GCL 模型通常遭受高计算成本的困扰。 然而,SVD 重建图的低秩性质和简化的 CL 结构使我们的 LightGCL训练非常高效。 我们分析了我们模型的预处理和每批训练的复杂性,并与三个竞争基线进行了比较,如表中所示。

RQ3:抵抗数据稀疏和流行度偏差
为了评估我们的模型在缓解数据稀疏性方面的稳健性,我们将稀疏用户按交互程度进行分组,并在 Yelp 和 Gowalla 数据集上计算每组的 Recall@20。 从图中可以看出,HCCF 和 SimGCL 的性能因数据集而异,但我们的 LightGCL 在所有情况下始终优于它们。 特别是,我们的模型在极其稀疏的用户组(< 15 个交互)上表现得非常好,因为这些用户的 Recall@20 并不比整个数据集低很多(在 Gowalla 上甚至更高)。下图左为数据稀疏比较,右为流行度偏差比较。

RQ3:过平滑和过均匀平衡


RQ4:消融实验

RQ4:Case分析

RQ5:超参分析


总结展望
本文通过设计一个轻量级且稳健的图对比学习框架来增强推荐系统。 具体来说,提出了一种有效且高效的对比学习范式 LightGCL,用于推荐系统中的图增强。 通过注入全局协作关系,该模型可以减轻不准确的对比自监督信号带来的问题。我们的主要发现表明,我们的图增强方案在抵抗数据稀疏性和流行度偏差方面表现出很强的能力。 大量实验表明,我们的模型在几个公共评估数据集上取得了新的最先进的结果。 在未来的工作中,我们计划探索将随意分析纳入我们的轻量级图对比学习模型的潜力,以增强推荐系统,减少数据增强的混淆效应。
参考资料
[1] Lianghao Xia, Chao Huang, Yong Xu, Jiashu Zhao, Dawei Yin, and Jimmy Xiangji Huang. Hypergraph contrastive collaborative filtering. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval, SIGIR 2022, Madrid, Spain, July 11-15, 2022., 2022a.
[2] Nathan Halko, Per-Gunnar Martinsson, and Joel A Tropp. Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions. SIAM review, 53 (2):217–288, 2011.
[3] Junliang Yu, Hongzhi Yin, Xin Xia, Tong Chen, Lizhen Cui, and Quoc Viet Hung Nguyen. Are graph augmentations necessary? simple graph contrastive learning for recommendation. In International Conference on Research and Development in Information Retrieval (SIGIR), pp. 1294–1303, 2022.