下面继续通过几个示例体会二进制枚举方法的应用。
【例1】建造碉堡
问题描述
设有一个街道笔直的方形城市。该城市的地图是一个有n行和n列的正方形,每行代表一条街道或一堵墙。
碉堡是一座有四个开口的小城堡,可以通过这些开口射击。四个开口分别面向北、东、南和西。每个开口都会有一支机枪射击。
假设一颗子弹威力巨大,它可以穿越任何距离,并在途中摧毁一座碉堡。另一方面,一堵墙是如此坚固,可以阻挡子弹。
你的目标是在该城市中建造尽可能多的碉堡,建造的碉堡要求任意两座碉堡都不会互相摧毁。也就是说没有两个碉堡位于同一水平行或垂直列上,除非至少有一堵墙将它们隔开。
例如,图1(a)是没有建造碉堡的初始初始状态(图中正方形黑块代表墙);图1(b)和(c)是建造可行方案(图中黑色实心圆代表建造的碉堡),图1(d)和(e)是建造不可行的方案。对图1(a)所示的城市状态,最多可以建造5座碉堡。图1(b)给出了一种可行的建造方案,当然还有其他几种建造方案。
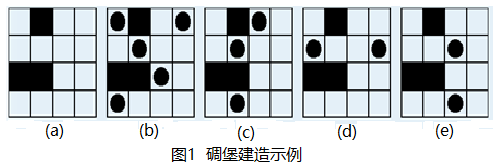
你的任务是编写一个程序,在给定地图描述的情况下,计算可以在城市中满足要求建造的碉堡的最大数量。
输入
输入包括多组测试用例。每组测试用例以包含正整数n的行开始,n是城市的大小,n最多为4。接下来的n行字符串分别描述地图的一行,其中字符“.”表示开放空间,大写字母“X”表示墙。输入字符串中没有空格。n=0,表示输入结束。
输出
对于每个测试用例,输出一行,其中包含可以在城市中满足要求建造的碉堡的最大数量。
输入样例
4
.X..
....
XX..
....
2
XX
.X
3
.X.
X.X
.X.
4
....
....
....
....
0
输出样例
5
1
5
4
(1)编程思路。
由于题目中n不大于4,地图中最多16个位置。因此,可以采用二进制枚举的方法,枚举在这n*n个位置中任选若干个位置建造碉堡的各种组合情况,然后对每个组合情况,逐个判断该组合情况中所建造的每个碉堡的可行性。
(2)源程序。
#include <stdio.h> #include <string.h> int n; char a[5][5]; int dir[4][2] = {1,0,0,1,-1,0,0,-1}; int judge(int x) // 判断计算二进制数表示的状态x中的1位是否都能建造碉堡,如不能返回1;否则返回可建造的碉堡个数 { char b[5][5]; int c[20], tot = 0; // 分别保存碉堡建造的位置和总个数 memcpy(b, a, sizeof(a)); int i,j; for (i = 0; i < n * n; i++) // 在二进制状态x中的1位建造碉堡 { if (x & (1 << i)) { int xx = i / n; int yy = i % n; if (b[xx][yy] == 'X') // 剪枝,如果碉堡建造在墙上,直接返回-1 return -1; b[xx][yy] = 'a'; // 建造碉堡 c[tot++] = i; } } for (i = 0; i < tot; i++) // 看建造的每个碉堡是否可行 { int x1 = c[i] / n; int y1 = c[i] % n; for (j = 0; j < 4; j++) // 四个方向遍历 { int x2 = x1 + dir[j][0]; int y2 = y1 + dir[j][1]; while(x2 >= 0 && x2 < n && y2 >= 0 && y2 < n)// 控制边界 { if(b[x2][y2] == 'X') break; // 碰到墙跳出循环 if(b[x2][y2] == 'a') return -1; // 碰到另一个碉堡'a',不可行 x2 += dir[j][0]; // 继续往这方向遍历 y2 += dir[j][1]; } } } return tot; } int main() { while(scanf("%d",&n) && n!=0) { int ans = 0; int i; for (i = 0; i < n; i++) scanf("%s",a[i]); for (i = 0; i < (1 << (n * n)); i++) // 二进制枚举地图各点建造碉堡的全部组合 { int cnt=judge(i); if (cnt>ans) ans = cnt; } printf("%d\n",ans); } return 0; }
将上面的源程序提交给HDU题库HDU 1045 Fire Net (http://acm.hdu.edu.cn/showproblem.php?pid=1045),可以Accepted。
【例2】子图像
问题描述
如果可以从图像B中删除一些行和一些列的像素,生成的图像与图像A相同,则称图像A是图像B的子图像。图2所示的图像A是图像B的子图像,因为从图像B中移除中间一行和中间一列的像素后,所产生的图像与A相同。
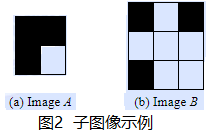
给定两个黑白图像A和B,确定A是否是B的子图像。
输入
输入第一行包含两个整数r和c(1≤ r、c≤ 20),表示图像A的行数和列数。以下r行,每行包含一个长度为c的字符串,给出一个r×c的0-1矩阵,表示图像A的像素。下一行包含两个整数R和C(r≤ R≤ 20,c≤ C≤ 20),表示图像B的行数和列数。以下R行,每行包含一个长度为C的字符串,给出一个代表图像B像素的R×C的0-1矩阵。0表示白色像素;1表示黑色像素。
输出
如果图像A是图像B的子图像,则输出“Yes”;否则,输出“No”。
输入样例
2 2
11
10
3 3
101
000
100
输出样例
Yes
(1)编程思路。
可以通过在图像B对应的0-1矩阵中寻找是否存在图像A所对应的0-1矩阵来判断图像A是否是图像B的子图像。
具体做法是:用二进制枚举矩阵B中R行的组合,若枚举的二进制数中1的个数正好为矩阵a的行数r,则表示可以在矩阵B的R行中选出矩阵A的r行。这种情况下,再用循环穷举的方法,看矩阵B的C列中,是否可以选出c列,矩阵B选中的r行在这c列上的值与矩阵A的值一致。
(2)源程序。
#include <stdio.h> int main() { char a[21][21],b[21][21]; int na,ma,nb,mb; scanf("%d%d",&na,&ma); int i,j,k; for (i=0; i<na; i++) scanf("%s",a[i]); scanf("%d%d",&nb,&mb); for (i=0; i<nb; i++) scanf("%s",b[i]); int flag=0,h[21]; for (k=0; k<(1<<nb); k++) // 二进制枚举B矩阵的行组合 { int cnt=0; for (j =0; j<nb; j++) // 遍历二进制的每一位 { if (k & (1 << j)) // 判断二进制第j位是否为1,若为1,表示行选中 h[cnt++]=j; // 如果第j个元素选中,则记录选中的行号 } if (cnt==na) // 矩阵B选中的行数正好是矩阵A的行数na { int st=0; // 矩阵B中可以挑选的起始列号 while (st<=mb-ma) { int cola=0,ff=1; for (i=st; i<mb; i++) // 从矩阵B的起始列到最后列中看能否找到矩阵A的所有列 { ff=1; for (j=0; j<na; j++) // 矩阵A中各行的当前列在矩阵B选中行的某列是否一致 if(a[j][cola]!=b[h[j]][i]) { ff=0; break; } if (ff) cola++; if (cola==ma) break; // A矩阵的ma列全部可在B矩阵中找到 } if (cola==ma) // A矩阵的ma列全部可在B矩阵中找到 { flag=1; break; } st++; // 当前起始列不恰当,将下一列作为起始列,重新找 } if (flag==1) break; // 已找到答案,退出循环 } } if (flag) printf("Yes\n"); else printf("No\n"); return 0; }
将上面的源程序提交给北大POJ题库POJ 3600 Subimage Recognition (http://poj.org/problem?id=3600),可以Accepted。
【例3】查找0-1矩阵
问题描述
给定一个M×N的0-1矩阵,你能找到一些让每个列包含且仅包含一个1的行吗。
输入
输入包括多组测试用例。每组测试用例的第一行输入为M,N(M≤ 16,N≤ 300),接下来的M行每行包含N个用空格分隔的整数0或1。
输出
对于每个测试用例,如果你能找到它,输出“Yes, I found it”,否则输出“It is impossible”。
输入样例
3 3
0 1 0
0 0 1
1 0 0
4 4
0 0 0 1
1 0 0 0
1 1 0 1
0 1 0 0
输出样例
Yes, I found it
It is impossible
(1)编程思路。
本题同样采用二进制枚举各行的组合,再用位运算来判断所选的那些行是否满足每列只有一个1。
由于题目中给出最多16行,因此可以用一个int型整数(32位>16)的每个二进制位来表示每列状态。以输入样例中的4×4矩阵来说明。第0列4行上的数字分别为0、1、1、0,对应二进制数为110,将其对应的十进制整数6保存到数组元素col[0]中,第1列4行上的数字分别为0、0、1、1,对应二进制数为1100,将其对应的十进制整数12保存到数组元素col[1]中;同理,col[2]=0,col[3]=5。
同样,对应输入样例中的3×3矩阵,则有 col[0]=4,col[1]=1,col[2]=2。
当二进制枚举到状态i时,要判断所选行中,第j列是否有且只有1个1。可以令t = col[j]&i,这样就把枚举的行里面的1取了出来。因为在枚举的二进制状态i中,选中的行相应位为1,未选中的行相应位为0,而 0 & 1=0,这样某列在未选中行上的1均会变成0。
得到t值后,如果t=0,说明枚举的这些行对应的某列里面一个1都不含,肯定不满足要求。如果 t != 0,再看 t&(t-1)的值,若该值等于0,表示 t 只有一个1,也就是在所选行中,第j列有且只有1个1;否则,t中不止1个1,不满足要求。
(2)源程序。
#include <stdio.h> #include <string.h> int main() { int m,n; while (scanf("%d%d", &m, &n)!=EOF){ int col[301]; int i,j,x,flag = 0; memset(col, 0, sizeof(col)); for (i=0; i<m; i ++){ // 输入时预处理,将每列中各行0、1组成的二进制数转换为十进制数保存到数组col中 for (j=0; j<n; j++){ scanf("%d",&x); if (x==1) col[j] += (1 << i); if (i==m-1 && col[j]==0) flag = 1; // 若每列1的个数为0,显然不可能 } } if (flag){ printf("It is impossible\n"); continue; } for (i=1; i<(1<<m); i++){ // 用二进制枚举,对各行的组合进行选择 for (j = 0; j < n; j ++){ int t = col[j] & i; if (t==0 || (t & (t-1))) { break; } } if (j==n) {flag = 1; break; } } if (flag == 0) printf("It is impossible\n"); else printf("Yes, I found it\n"); } return 0; }
将上面的源程序提交给北大POJ题库POJ 3740 Easy Finding(http://poj.org/problem?id=3740),可以Accepted。